# ThymeBoost v0.1.16
## Changes with 1.16:
New Trend Estimators: 'lbf' and 'decision_tree'. 'lbf' stands for linear basis functions and will fit a linear changepoint method with a similar vibe to that of Prophet. When this is boosted it gets much more smooth.
[](https://thymeboost.readthedocs.io/en/latest/?badge=latest) [](https://pepy.tech/project/thymeboost)
ThymeBoost combines time series decomposition with gradient boosting to provide a flexible mix-and-match time series framework for forecasting. At the most granular level are the trend/level (going forward this is just referred to as 'trend') models, seasonal models, and endogenous models. These are used to approximate the respective components at each 'boosting round' and sequential rounds are fit on residuals in usual boosting fashion.
Documentation is under construction at : https://thymeboost.readthedocs.io/en/latest/
## Basic flow of the algorithm:
## Quick Start.
```
pip install ThymeBoost
```
## Some basic examples:
Starting with a very simple example of a simple trend + seasonality + noise
```
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns
from ThymeBoost import ThymeBoost as tb
sns.set_style('darkgrid')
#Here we will just create a random series with seasonality and a slight trend
seasonality = ((np.cos(np.arange(1, 101))*10 + 50))
np.random.seed(100)
true = np.linspace(-1, 1, 100)
noise = np.random.normal(0, 1, 100)
y = true + noise + seasonality
plt.plot(y)
plt.show()
```
First we will build the ThymeBoost model object:
```
boosted_model = tb.ThymeBoost(approximate_splits=True,
n_split_proposals=25,
verbose=1,
cost_penalty=.001)
```
The arguments passed here are also the defaults. Most importantly, we pass whether we want to use 'approximate splits' and how many splits to propose. If we pass ```approximate_splits=False``` then ThymeBoost will exhaustively try every data point to split on if we look for changepoints. If we don't care about changepoints then this is ignored.
ThymeBoost uses a standard fit => predict procedure. Let's use the fit method where everything passed is converted to a itertools cycle object in ThymeBoost, this will be referred as 'generator' parameters moving forward. This might not make sense yet but is shown further in the examples!
```
output = boosted_model.fit(y,
trend_estimator='linear',
seasonal_estimator='fourier',
seasonal_period=25,
split_cost='mse',
global_cost='maicc',
fit_type='global')
```
We pass the input time_series and the parameters used to fit. For ThymeBoost the more specific parameters are the different cost functions controlling for each split and the global cost function which controls how many boosting rounds to do. Additionally, the ```fit_type='global'``` designates that we are NOT looking for changepoints and just fits our trend_estimator globally.
With verbose ThymeBoost will print out some relevant information for us.
Now that we have fitted our series we can take a look at our results
```
boosted_model.plot_results(output)
```
The fit looks correct enough, but let's take a look at the indiviudal components we fitted.
```
boosted_model.plot_components(output)
```
Alright, the decomposition looks reasonable as well but let's complicate the task by now adding a changepoint.
## Adding a changepoint
```
true = np.linspace(1, 50, 100)
noise = np.random.normal(0, 1, 100)
y = np.append(y, true + noise + seasonality)
plt.plot(y)
plt.show()
```
In order to fit this we will change ```fit_type='global'``` to ```fit_type='local'```. Let's see what happens.
```
boosted_model = tb.ThymeBoost(
approximate_splits=True,
n_split_proposals=25,
verbose=1,
cost_penalty=.001,
)
output = boosted_model.fit(y,
trend_estimator='linear',
seasonal_estimator='fourier',
seasonal_period=25,
split_cost='mse',
global_cost='maicc',
fit_type='local')
predicted_output = boosted_model.predict(output, 100)
```
Here we add in the predict method which takes in the fitted results as well as the forecast horizon. You will notice that the print out now states we are fitting locally and we do an additional round of boosting. Let's plot the results and see if the new round was ThymeBoost picking up the changepoint.
```
boosted_model.plot_results(output, predicted_output)
```
Ok, cool. Looks like it worked about as expected here, we did do 1 wasted round where ThymeBoost just did a slight adjustment at split 80 but that can be fixed as you will see!
Once again looking at the components:
```
boosted_model.plot_components(output)
```
There is a kink in the trend right around 100 as to be expected.
Let's further complicate this series.
## Adding a large jump
```
#Pretty complicated model
true = np.linspace(1, 20, 100) + 100
noise = np.random.normal(0, 1, 100)
y = np.append(y, true + noise + seasonality)
plt.plot(y)
plt.show()
```
So here we have 3 distinct trend lines and one large shift upward. Overall, pretty nasty and automatically fitting this with any model (including ThymeBoost) can have extremely wonky results.
But...let's try anyway. Here we will utilize the 'generator' variables. As mentioned before, everything passed in to the fit method is a generator variable. This basically means that we can pass a list for a parameter and that list will be cycled through at each boosting round. So if we pass this: ```trend_estimator=['mean', 'linear']``` after the initial trend estimation using the median we then use mean followed by linear then mean and linear until boosting is terminated. We can also use this to approximate a potential complex seasonality just by passing a list of what the complex seasonality can be. Let's fit with these generator variables and pay close attention to the print out as it will show you what ThymeBoost is doing at each round.
```
boosted_model = tb.ThymeBoost(
approximate_splits=True,
verbose=1,
cost_penalty=.001,
)
output = boosted_model.fit(y,
trend_estimator=['mean'] + ['linear']*20,
seasonal_estimator='fourier',
seasonal_period=[25, 0],
split_cost='mae',
global_cost='maicc',
fit_type='local',
connectivity_constraint=True,
)
predicted_output = boosted_model.predict(output, 100)
```
The log tells us what we need to know:
```
********** Round 1 **********
Using Split: None
Fitting initial trend globally with trend model:
median()
seasonal model:
fourier(10, False)
cost: 2406.7734967780552
********** Round 2 **********
Using Split: 200
Fitting local with trend model:
mean()
seasonal model:
None
cost: 1613.03414289753
********** Round 3 **********
Using Split: 174
Fitting local with trend model:
linear((1, None))
seasonal model:
fourier(10, False)
cost: 1392.923553270366
********** Round 4 **********
Using Split: 274
Fitting local with trend model:
linear((1, None))
seasonal model:
None
cost: 1384.306737800115
==============================
Boosting Terminated
Using round 4
```
The initial round for trend is always the same (this idea is pretty core to the boosting framework) but after that we fit with mean and the next 2 rounds are fit with linear estimation. The complex seasonality works 100% as we expect, just going back and forth between the 2 periods we give it where a 0 period means no seasonality estimation occurs.
Let's take a look at the results:
```
boosted_model.plot_results(output, predicted_output)
```
Hmmm, that looks very wonky.
But since we used a mean estimator we are saying that there is a change in the overall level of the series. That's not exactly true, by appending that last series with just another trend line we essentially changed the slope and the intercept of the series.
To account for this, let's relax connectivity constraints and just try linear estimators. Once again, EVERYTHING passed to the fit method is a generator variable so we will relax the connectivity constraint for the first linear fit to hopefully account for the large jump. After that we will use the constraint for 10 rounds then ThymeBoost will just cycle through the list we provide again.
```
#Without connectivity constraint
boosted_model = tb.ThymeBoost(
approximate_splits=True,
verbose=1,
cost_penalty=.001,
)
output = boosted_model.fit(y,
trend_estimator='linear',
seasonal_estimator='fourier',
seasonal_period=[25, 0],
split_cost='mae',
global_cost='maicc',
fit_type='local',
connectivity_constraint=[False] + [True]*10,
)
predicted_output = boosted_model.predict(output, 100)
boosted_model.plot_results(output, predicted_output)
```
Alright, that looks a ton better. It does have some underfitting going on in the middle which is typical since we are using binary segmentation for the changepoints. But other than that it seems reasonable. Let's take a look at the components:
```
boosted_model.plot_components(output)
```
Looks like the model is catching on to the underlying process creating the data. The trend is clearly composed of three segments and has that large jump right at 200 just as we hoped to see!
## Controlling the boosting rounds
We can control how many rounds and therefore the complexity of our model a couple of different ways. The most direct is by controlling the number of rounds.
```
#n_rounds=1
boosted_model = tb.ThymeBoost(
approximate_splits=True,
verbose=1,
cost_penalty=.001,
n_rounds=1
)
output = boosted_model.fit(y,
trend_estimator='arima',
arima_order=[(1, 0, 0), (1, 0, 1), (1, 1, 1)],
seasonal_estimator='fourier',
seasonal_period=25,
split_cost='mae',
global_cost='maicc',
fit_type='global',
)
predicted_output = boosted_model.predict(output, 100)
boosted_model.plot_components(output)
```
By passing ```n_rounds=1``` we only allow ThymeBoost to do the initial trend estimation (a simple median) and one shot at approximating the seasonality.
Additionally we are trying out a new ```trend_estimator``` along with the related parameter ```arima_order```. Although we didn't get to it we are passing the ```arima_order``` to go from simple to complex.
Let's try forcing ThymeBoost to go through all of our provided ARIMA orders by setting ```n_rounds=4```
```
boosted_model = tb.ThymeBoost(
approximate_splits=True,
verbose=1,
cost_penalty=.001,
n_rounds=4,
regularization=1.2
)
output = boosted_model.fit(y,
trend_estimator='arima',
arima_order=[(1, 0, 0), (1, 0, 1), (1, 1, 1)],
seasonal_estimator='fourier',
seasonal_period=25,
split_cost='mae',
global_cost='maicc',
fit_type='global',
)
predicted_output = boosted_model.predict(output, 100)
```
Looking at the log:
```
********** Round 1 **********
Using Split: None
Fitting initial trend globally with trend model:
median()
seasonal model:
fourier(10, False)
cost: 2406.7734967780552
********** Round 2 **********
Using Split: None
Fitting global with trend model:
arima((1, 0, 0))
seasonal model:
fourier(10, False)
cost: 988.0694403606061
********** Round 3 **********
Using Split: None
Fitting global with trend model:
arima((1, 0, 1))
seasonal model:
fourier(10, False)
cost: 991.7292716360867
********** Round 4 **********
Using Split: None
Fitting global with trend model:
arima((1, 1, 1))
seasonal model:
fourier(10, False)
cost: 1180.688829140743
```
We can see that the cost which typically controls boosting is ignored. It actually increases in round 3. An alternative for boosting complexity would be to pass a larger ```regularization``` parameter when building the model class.
## Component Regularization with a Learning Rate
Another idea taken from gradient boosting is the use of a learning rate. However, we allow component-specific learning rates. The main benefit to this is that it allows us to have the same fitting procedure (always trend => seasonality => exogenous) but account for the potential different ways we want to fit. For example, let's say our series is responding to an exogenous variable that is seasonal. Since we fit for seasonality BEFORE exogenous then we could eat up that signal. However, we could simply pass a ```seasonality_lr``` (or trend_lr / exogenous_lr) which will penalize the seasonality approximation and leave the signal for the exogenous component fit.
Here is a quick example, as always we could pass it as a list if we want to allow seasonality to return to normal after the first round.
```
#seasonality regularization
boosted_model = tb.ThymeBoost(
approximate_splits=True,
verbose=1,
cost_penalty=.001,
n_rounds=2
)
output = boosted_model.fit(y,
trend_estimator='arima',
arima_order=(1, 0, 1),
seasonal_estimator='fourier',
seasonal_period=25,
split_cost='mae',
global_cost='maicc',
fit_type='global',
seasonality_lr=.1
)
predicted_output = boosted_model.predict(output, 100)
```
## Parameter Optimization
ThymeBoost has an optimizer which will try to find the 'optimal' parameter settings based on all combinations that are passed.
Importantly, all parameters that are normally pass to fit must now be passed as a list.
Let's take a look:
```
boosted_model = tb.ThymeBoost(
approximate_splits=True,
verbose=0,
cost_penalty=.001,
)
output = boosted_model.optimize(y,
verbose=1,
lag=20,
optimization_steps=1,
trend_estimator=['mean', 'linear', ['mean', 'linear']],
seasonal_period=[0, 25],
fit_type=['local', 'global'])
```
```
100%|██████████| 12/12 [00:00<00:00, 46.63it/s]
Optimal model configuration: {'trend_estimator': 'linear', 'fit_type': 'local', 'seasonal_period': 25, 'exogenous': None}
Params ensembled: False
```
First off, I disabled the verbose call in the constructor so it won't print out everything for each model. Instead, passing ```verbose=1``` to the optimize method will print a tqdm progress bar and the best model configuration. Lag refers to the number of points to holdout for our test set and optimization_steps allows you to roll through the holdout.
Another important thing to note, one of the elements in the list of trend_estimators is itself a list. With optimization, all we do is try each combination of the parameters given so each element in the list provided will be passed to the normal fit method, if that element is a list then that means you are using a generator variable for that implementation.
With the optimizer class we retain all other methods we have been using after fit.
```
predicted_output = boosted_model.predict(output, 100)
boosted_model.plot_results(output, predicted_output)
```
So this output looks wonky around that changepoint but it recovers in time to produce a good enough forecast to do well in the holdout.
## Ensembling
Instead of iterating through and choosing the best parameters we could also just ensemble them into a simple average of every parameter setting.
Everything stated about the optimizer holds for ensemble as well, except now we just call the ensemble method.
```
boosted_model = tb.ThymeBoost(
approximate_splits=True,
verbose=0,
cost_penalty=.001,
)
output = boosted_model.ensemble(y,
trend_estimator=['mean', 'linear', ['mean', 'linear']],
seasonal_period=[0, 25],
fit_type=['local', 'global'])
predicted_output = boosted_model.predict(output, 100)
boosted_model.plot_results(output, predicted_output)
```
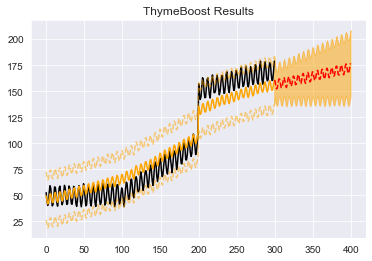
Obviously, this output is quite wonky. Primarily because of the 'global' parameter which is pulling everything to the center of the data. However, ensembling has been shown to be quite effective in the wild.
## Optimization with Ensembling?
So what if we want to try an ensemble out during optimization, is that possible?
The answer is yes!
But to do it we have to use a new function in our optimize method. Here is an example:
```
boosted_model = tb.ThymeBoost(
approximate_splits=True,
verbose=0,
cost_penalty=.001,
)
output = boosted_model.optimize(y,
lag=10,
optimization_steps=1,
trend_estimator=['mean', boosted_model.combine(['ses', 'des', 'damped_des'])],
seasonal_period=[0, 25],
fit_type=['global'])
predicted_output = boosted_model.predict(output, 100)
```
For everything we want to be treated as an ensemble while optimizing we must wrap the parameter list in the combine function as seen: ```boosted_model.combine(['ses', 'des', 'damped_des'])```
And now in the log:
```
Optimal model configuration: {'trend_estimator': ['ses', 'des', 'damped_des'], 'fit_type': ['global'], 'seasonal_period': [25], 'exogenous': [None]}
Params ensembled: True
```
We see that everything returned is a list and 'Params ensembled' is now True, signifying to ThymeBoost that this is an Ensemble.
Let's take a look at the outputs:
```
boosted_model.plot_results(output, predicted_output)
```
# ToDo
The package is still under heavy development and with the large number of combinations that arise from the framework if you find any issues definitely raise them!
Logging and error handling is still basic to non-existent, so it is one of our top priorities.
Raw data
{
"_id": null,
"home_page": "https://github.com/tblume1992/ThymeBoost",
"name": "ThymeBoost",
"maintainer": "",
"docs_url": null,
"requires_python": "",
"maintainer_email": "",
"keywords": "forecasting,time series,seasonality,trend",
"author": "Tyler Blume",
"author_email": "t-blume@hotmail.com",
"download_url": "",
"platform": null,
"description": "# ThymeBoost v0.1.16\n\n## Changes with 1.16:\n\nNew Trend Estimators: 'lbf' and 'decision_tree'. 'lbf' stands for linear basis functions and will fit a linear changepoint method with a similar vibe to that of Prophet. When this is boosted it gets much more smooth.\n\n\n[](https://thymeboost.readthedocs.io/en/latest/?badge=latest) [](https://pepy.tech/project/thymeboost)\n\n![alt text](https://github.com/tblume1992/ThymeBoost/blob/main/static/tb_logo.png?raw=true \"Output 1\")\n\nThymeBoost combines time series decomposition with gradient boosting to provide a flexible mix-and-match time series framework for forecasting. At the most granular level are the trend/level (going forward this is just referred to as 'trend') models, seasonal models, and endogenous models. These are used to approximate the respective components at each 'boosting round' and sequential rounds are fit on residuals in usual boosting fashion.\n\nDocumentation is under construction at : https://thymeboost.readthedocs.io/en/latest/\n\n## Basic flow of the algorithm:\n\n![alt text](https://github.com/tblume1992/ThymeBoost/blob/main/static/thymeboost_flow.png?raw=true \"Output 1\")\n\n\n## Quick Start.\n\n```\npip install ThymeBoost\n```\n\n\n\n## Some basic examples:\nStarting with a very simple example of a simple trend + seasonality + noise\n```\nimport numpy as np\nimport matplotlib.pyplot as plt\nimport seaborn as sns\nfrom ThymeBoost import ThymeBoost as tb\n\nsns.set_style('darkgrid')\n\n#Here we will just create a random series with seasonality and a slight trend\nseasonality = ((np.cos(np.arange(1, 101))*10 + 50))\nnp.random.seed(100)\ntrue = np.linspace(-1, 1, 100)\nnoise = np.random.normal(0, 1, 100)\ny = true + noise + seasonality\nplt.plot(y)\nplt.show()\n\n```\n\n\n\nFirst we will build the ThymeBoost model object:\n```\nboosted_model = tb.ThymeBoost(approximate_splits=True,\n n_split_proposals=25,\n verbose=1,\n cost_penalty=.001)\n```\nThe arguments passed here are also the defaults. Most importantly, we pass whether we want to use 'approximate splits' and how many splits to propose. If we pass ```approximate_splits=False``` then ThymeBoost will exhaustively try every data point to split on if we look for changepoints. If we don't care about changepoints then this is ignored.\n\nThymeBoost uses a standard fit => predict procedure. Let's use the fit method where everything passed is converted to a itertools cycle object in ThymeBoost, this will be referred as 'generator' parameters moving forward. This might not make sense yet but is shown further in the examples!\n```\noutput = boosted_model.fit(y,\n trend_estimator='linear',\n seasonal_estimator='fourier',\n seasonal_period=25,\n split_cost='mse',\n global_cost='maicc',\n fit_type='global')\n```\nWe pass the input time_series and the parameters used to fit. For ThymeBoost the more specific parameters are the different cost functions controlling for each split and the global cost function which controls how many boosting rounds to do. Additionally, the ```fit_type='global'``` designates that we are NOT looking for changepoints and just fits our trend_estimator globally.\n\nWith verbose ThymeBoost will print out some relevant information for us.\n\nNow that we have fitted our series we can take a look at our results\n```\nboosted_model.plot_results(output)\n```\n\n![alt text](https://github.com/tblume1992/ThymeBoost/blob/main/static/tb_output_1.png?raw=true \"Output 1\")\n\nThe fit looks correct enough, but let's take a look at the indiviudal components we fitted.\n```\nboosted_model.plot_components(output)\n```\n\n![alt text](https://github.com/tblume1992/ThymeBoost/blob/main/static/tb_components_1.png?raw=true \"Output 1\")\n\nAlright, the decomposition looks reasonable as well but let's complicate the task by now adding a changepoint.\n\n\n## Adding a changepoint\n```\ntrue = np.linspace(1, 50, 100)\nnoise = np.random.normal(0, 1, 100)\ny = np.append(y, true + noise + seasonality)\nplt.plot(y)\nplt.show()\n```\n\n![alt text](https://github.com/tblume1992/ThymeBoost/blob/main/static/time_series_2.png?raw=true \"Output 1\")\n\nIn order to fit this we will change ```fit_type='global'``` to ```fit_type='local'```. Let's see what happens.\n\n```\nboosted_model = tb.ThymeBoost(\n approximate_splits=True,\n n_split_proposals=25,\n verbose=1,\n cost_penalty=.001,\n )\n\noutput = boosted_model.fit(y,\n trend_estimator='linear',\n seasonal_estimator='fourier',\n seasonal_period=25,\n split_cost='mse',\n global_cost='maicc',\n fit_type='local')\npredicted_output = boosted_model.predict(output, 100)\n```\nHere we add in the predict method which takes in the fitted results as well as the forecast horizon. You will notice that the print out now states we are fitting locally and we do an additional round of boosting. Let's plot the results and see if the new round was ThymeBoost picking up the changepoint.\n\n```\nboosted_model.plot_results(output, predicted_output)\n```\n\n![alt text](https://github.com/tblume1992/ThymeBoost/blob/main/static/tb_output_2.png?raw=true \"Output 1\")\n\n\nOk, cool. Looks like it worked about as expected here, we did do 1 wasted round where ThymeBoost just did a slight adjustment at split 80 but that can be fixed as you will see!\n\nOnce again looking at the components:\n```\nboosted_model.plot_components(output)\n```\n\n![alt text](https://github.com/tblume1992/ThymeBoost/blob/main/static/tb_components_2.png?raw=true \"Output 1\")\n\n\nThere is a kink in the trend right around 100 as to be expected.\n\nLet's further complicate this series.\n\n## Adding a large jump\n\n```\n#Pretty complicated model\ntrue = np.linspace(1, 20, 100) + 100\nnoise = np.random.normal(0, 1, 100)\ny = np.append(y, true + noise + seasonality)\nplt.plot(y)\nplt.show()\n```\n\n![alt text](https://github.com/tblume1992/ThymeBoost/blob/main/static/complicated_time_series.png?raw=true \"Output 1\")\n\n\nSo here we have 3 distinct trend lines and one large shift upward. Overall, pretty nasty and automatically fitting this with any model (including ThymeBoost) can have extremely wonky results.\n\nBut...let's try anyway. Here we will utilize the 'generator' variables. As mentioned before, everything passed in to the fit method is a generator variable. This basically means that we can pass a list for a parameter and that list will be cycled through at each boosting round. So if we pass this: ```trend_estimator=['mean', 'linear']``` after the initial trend estimation using the median we then use mean followed by linear then mean and linear until boosting is terminated. We can also use this to approximate a potential complex seasonality just by passing a list of what the complex seasonality can be. Let's fit with these generator variables and pay close attention to the print out as it will show you what ThymeBoost is doing at each round.\n\n```\nboosted_model = tb.ThymeBoost(\n approximate_splits=True,\n verbose=1,\n cost_penalty=.001,\n )\n\noutput = boosted_model.fit(y,\n trend_estimator=['mean'] + ['linear']*20,\n seasonal_estimator='fourier',\n seasonal_period=[25, 0],\n split_cost='mae',\n global_cost='maicc',\n fit_type='local',\n connectivity_constraint=True,\n )\n\npredicted_output = boosted_model.predict(output, 100)\n\n```\n\nThe log tells us what we need to know:\n\n```\n********** Round 1 **********\nUsing Split: None\nFitting initial trend globally with trend model:\nmedian()\nseasonal model:\nfourier(10, False)\ncost: 2406.7734967780552\n********** Round 2 **********\nUsing Split: 200\nFitting local with trend model:\nmean()\nseasonal model:\nNone\ncost: 1613.03414289753\n********** Round 3 **********\nUsing Split: 174\nFitting local with trend model:\nlinear((1, None))\nseasonal model:\nfourier(10, False)\ncost: 1392.923553270366\n********** Round 4 **********\nUsing Split: 274\nFitting local with trend model:\nlinear((1, None))\nseasonal model:\nNone\ncost: 1384.306737800115\n==============================\nBoosting Terminated \nUsing round 4\n```\n\nThe initial round for trend is always the same (this idea is pretty core to the boosting framework) but after that we fit with mean and the next 2 rounds are fit with linear estimation. The complex seasonality works 100% as we expect, just going back and forth between the 2 periods we give it where a 0 period means no seasonality estimation occurs.\n\nLet's take a look at the results:\n\n```\nboosted_model.plot_results(output, predicted_output)\n```\n\n![alt text](https://github.com/tblume1992/ThymeBoost/blob/main/static/complicated_output_bad.png?raw=true \"Output 1\")\n\nHmmm, that looks very wonky.\n\nBut since we used a mean estimator we are saying that there is a change in the overall level of the series. That's not exactly true, by appending that last series with just another trend line we essentially changed the slope and the intercept of the series.\n\nTo account for this, let's relax connectivity constraints and just try linear estimators. Once again, EVERYTHING passed to the fit method is a generator variable so we will relax the connectivity constraint for the first linear fit to hopefully account for the large jump. After that we will use the constraint for 10 rounds then ThymeBoost will just cycle through the list we provide again.\n\n```\n#Without connectivity constraint\nboosted_model = tb.ThymeBoost(\n approximate_splits=True,\n verbose=1,\n cost_penalty=.001,\n )\n\noutput = boosted_model.fit(y,\n trend_estimator='linear',\n seasonal_estimator='fourier',\n seasonal_period=[25, 0],\n split_cost='mae',\n global_cost='maicc',\n fit_type='local',\n connectivity_constraint=[False] + [True]*10,\n )\npredicted_output = boosted_model.predict(output, 100)\nboosted_model.plot_results(output, predicted_output)\n```\n\n![alt text](https://github.com/tblume1992/ThymeBoost/blob/main/static/tb_complicated_output.png?raw=true \"Output 1\")\n\nAlright, that looks a ton better. It does have some underfitting going on in the middle which is typical since we are using binary segmentation for the changepoints. But other than that it seems reasonable. Let's take a look at the components:\n\n```\nboosted_model.plot_components(output)\n```\n\n![alt text](https://github.com/tblume1992/ThymeBoost/blob/main/static/complicated_components.png?raw=true \"Output 1\")\n\n\nLooks like the model is catching on to the underlying process creating the data. The trend is clearly composed of three segments and has that large jump right at 200 just as we hoped to see!\n\n## Controlling the boosting rounds\n\nWe can control how many rounds and therefore the complexity of our model a couple of different ways. The most direct is by controlling the number of rounds.\n```\n#n_rounds=1\nboosted_model = tb.ThymeBoost(\n approximate_splits=True,\n verbose=1,\n cost_penalty=.001,\n n_rounds=1\n )\n\noutput = boosted_model.fit(y,\n trend_estimator='arima',\n arima_order=[(1, 0, 0), (1, 0, 1), (1, 1, 1)],\n seasonal_estimator='fourier',\n seasonal_period=25,\n split_cost='mae',\n global_cost='maicc',\n fit_type='global',\n )\npredicted_output = boosted_model.predict(output, 100)\nboosted_model.plot_components(output)\n```\n\n![alt text](https://github.com/tblume1992/ThymeBoost/blob/main/static/n_rounds1.png?raw=true \"Output 1\")\n\n\nBy passing ```n_rounds=1``` we only allow ThymeBoost to do the initial trend estimation (a simple median) and one shot at approximating the seasonality.\n\nAdditionally we are trying out a new ```trend_estimator``` along with the related parameter ```arima_order```. Although we didn't get to it we are passing the ```arima_order``` to go from simple to complex.\n\nLet's try forcing ThymeBoost to go through all of our provided ARIMA orders by setting ```n_rounds=4```\n\n```\nboosted_model = tb.ThymeBoost(\n approximate_splits=True,\n verbose=1,\n cost_penalty=.001,\n n_rounds=4,\n regularization=1.2\n )\n\noutput = boosted_model.fit(y,\n trend_estimator='arima',\n arima_order=[(1, 0, 0), (1, 0, 1), (1, 1, 1)],\n seasonal_estimator='fourier',\n seasonal_period=25,\n split_cost='mae',\n global_cost='maicc',\n fit_type='global',\n )\npredicted_output = boosted_model.predict(output, 100)\n```\n\nLooking at the log:\n\n```\n********** Round 1 **********\nUsing Split: None\nFitting initial trend globally with trend model:\nmedian()\nseasonal model:\nfourier(10, False)\ncost: 2406.7734967780552\n********** Round 2 **********\nUsing Split: None\nFitting global with trend model:\narima((1, 0, 0))\nseasonal model:\nfourier(10, False)\ncost: 988.0694403606061\n********** Round 3 **********\nUsing Split: None\nFitting global with trend model:\narima((1, 0, 1))\nseasonal model:\nfourier(10, False)\ncost: 991.7292716360867\n********** Round 4 **********\nUsing Split: None\nFitting global with trend model:\narima((1, 1, 1))\nseasonal model:\nfourier(10, False)\ncost: 1180.688829140743\n```\n\nWe can see that the cost which typically controls boosting is ignored. It actually increases in round 3. An alternative for boosting complexity would be to pass a larger ```regularization``` parameter when building the model class.\n\n## Component Regularization with a Learning Rate\n\nAnother idea taken from gradient boosting is the use of a learning rate. However, we allow component-specific learning rates. The main benefit to this is that it allows us to have the same fitting procedure (always trend => seasonality => exogenous) but account for the potential different ways we want to fit. For example, let's say our series is responding to an exogenous variable that is seasonal. Since we fit for seasonality BEFORE exogenous then we could eat up that signal. However, we could simply pass a ```seasonality_lr``` (or trend_lr / exogenous_lr) which will penalize the seasonality approximation and leave the signal for the exogenous component fit.\n\nHere is a quick example, as always we could pass it as a list if we want to allow seasonality to return to normal after the first round.\n\n```\n#seasonality regularization\nboosted_model = tb.ThymeBoost(\n approximate_splits=True,\n verbose=1,\n cost_penalty=.001,\n n_rounds=2\n )\n\noutput = boosted_model.fit(y,\n trend_estimator='arima',\n arima_order=(1, 0, 1),\n seasonal_estimator='fourier',\n seasonal_period=25,\n split_cost='mae',\n global_cost='maicc',\n fit_type='global',\n seasonality_lr=.1\n )\npredicted_output = boosted_model.predict(output, 100)\n```\n\n## Parameter Optimization\n\nThymeBoost has an optimizer which will try to find the 'optimal' parameter settings based on all combinations that are passed.\n\nImportantly, all parameters that are normally pass to fit must now be passed as a list.\n\nLet's take a look:\n\n```\nboosted_model = tb.ThymeBoost(\n approximate_splits=True,\n verbose=0,\n cost_penalty=.001,\n )\n\noutput = boosted_model.optimize(y, \n verbose=1,\n lag=20,\n optimization_steps=1,\n trend_estimator=['mean', 'linear', ['mean', 'linear']],\n seasonal_period=[0, 25],\n fit_type=['local', 'global'])\n```\n\n```\n100%|\u00e2\u2013\u02c6\u00e2\u2013\u02c6\u00e2\u2013\u02c6\u00e2\u2013\u02c6\u00e2\u2013\u02c6\u00e2\u2013\u02c6\u00e2\u2013\u02c6\u00e2\u2013\u02c6\u00e2\u2013\u02c6\u00e2\u2013\u02c6| 12/12 [00:00<00:00, 46.63it/s]\nOptimal model configuration: {'trend_estimator': 'linear', 'fit_type': 'local', 'seasonal_period': 25, 'exogenous': None}\nParams ensembled: False\n```\n\n\nFirst off, I disabled the verbose call in the constructor so it won't print out everything for each model. Instead, passing ```verbose=1``` to the optimize method will print a tqdm progress bar and the best model configuration. Lag refers to the number of points to holdout for our test set and optimization_steps allows you to roll through the holdout.\n\nAnother important thing to note, one of the elements in the list of trend_estimators is itself a list. With optimization, all we do is try each combination of the parameters given so each element in the list provided will be passed to the normal fit method, if that element is a list then that means you are using a generator variable for that implementation.\n\nWith the optimizer class we retain all other methods we have been using after fit.\n\n```\npredicted_output = boosted_model.predict(output, 100)\n\nboosted_model.plot_results(output, predicted_output)\n```\n\n![alt text](https://github.com/tblume1992/ThymeBoost/blob/main/static/optimizer_output.png?raw=true \"Output 1\")\n\nSo this output looks wonky around that changepoint but it recovers in time to produce a good enough forecast to do well in the holdout.\n\n## Ensembling\n\nInstead of iterating through and choosing the best parameters we could also just ensemble them into a simple average of every parameter setting.\n\nEverything stated about the optimizer holds for ensemble as well, except now we just call the ensemble method.\n\n```\nboosted_model = tb.ThymeBoost(\n approximate_splits=True,\n verbose=0,\n cost_penalty=.001,\n )\n\noutput = boosted_model.ensemble(y, \n trend_estimator=['mean', 'linear', ['mean', 'linear']],\n seasonal_period=[0, 25],\n fit_type=['local', 'global'])\n\npredicted_output = boosted_model.predict(output, 100)\n\nboosted_model.plot_results(output, predicted_output)\n```\n\n\n\nObviously, this output is quite wonky. Primarily because of the 'global' parameter which is pulling everything to the center of the data. However, ensembling has been shown to be quite effective in the wild.\n\n## Optimization with Ensembling?\n\nSo what if we want to try an ensemble out during optimization, is that possible?\n\nThe answer is yes!\n\nBut to do it we have to use a new function in our optimize method. Here is an example:\n\n```\nboosted_model = tb.ThymeBoost(\n approximate_splits=True,\n verbose=0,\n cost_penalty=.001,\n )\n\noutput = boosted_model.optimize(y, \n lag=10,\n optimization_steps=1,\n trend_estimator=['mean', boosted_model.combine(['ses', 'des', 'damped_des'])],\n seasonal_period=[0, 25],\n fit_type=['global'])\n\npredicted_output = boosted_model.predict(output, 100)\n```\n\nFor everything we want to be treated as an ensemble while optimizing we must wrap the parameter list in the combine function as seen: ```boosted_model.combine(['ses', 'des', 'damped_des'])```\n\nAnd now in the log:\n\n```\nOptimal model configuration: {'trend_estimator': ['ses', 'des', 'damped_des'], 'fit_type': ['global'], 'seasonal_period': [25], 'exogenous': [None]}\nParams ensembled: True\n```\n\nWe see that everything returned is a list and 'Params ensembled' is now True, signifying to ThymeBoost that this is an Ensemble.\n\nLet's take a look at the outputs:\n```\nboosted_model.plot_results(output, predicted_output)\n```\n\n![alt text](https://github.com/tblume1992/ThymeBoost/blob/main/static/optimized_ensemble.png?raw=true \"Output 1\")\n\n\n# ToDo\n\nThe package is still under heavy development and with the large number of combinations that arise from the framework if you find any issues definitely raise them!\n\nLogging and error handling is still basic to non-existent, so it is one of our top priorities.\n",
"bugtrack_url": null,
"license": "",
"summary": "Gradient boosted time series decomposition for forecasting.",
"version": "0.1.18",
"project_urls": {
"Homepage": "https://github.com/tblume1992/ThymeBoost"
},
"split_keywords": [
"forecasting",
"time series",
"seasonality",
"trend"
],
"urls": [
{
"comment_text": "",
"digests": {
"blake2b_256": "b6e59195c06aafda42f475dcd47b3b68dda862c37dc5f614d3cf988d5dd5f49d",
"md5": "bff3262e352eea8d427383c17749c6fd",
"sha256": "6fb73a44086f257420ef6dc2a1080815a7e20b4d49530524213256b999393c50"
},
"downloads": -1,
"filename": "ThymeBoost-0.1.18-py3-none-any.whl",
"has_sig": false,
"md5_digest": "bff3262e352eea8d427383c17749c6fd",
"packagetype": "bdist_wheel",
"python_version": "py3",
"requires_python": null,
"size": 67837,
"upload_time": "2024-01-04T02:36:02",
"upload_time_iso_8601": "2024-01-04T02:36:02.992717Z",
"url": "https://files.pythonhosted.org/packages/b6/e5/9195c06aafda42f475dcd47b3b68dda862c37dc5f614d3cf988d5dd5f49d/ThymeBoost-0.1.18-py3-none-any.whl",
"yanked": false,
"yanked_reason": null
}
],
"upload_time": "2024-01-04 02:36:02",
"github": true,
"gitlab": false,
"bitbucket": false,
"codeberg": false,
"github_user": "tblume1992",
"github_project": "ThymeBoost",
"travis_ci": false,
"coveralls": false,
"github_actions": false,
"lcname": "thymeboost"
}
JSON
