# `auto-period-finder`
[](https://pypi.org/project/auto-period-finder/)


## About `auto-period-finder`
`auto-period-finder` is an autocorrelation function (ACF) based seasonality periods automatic finder for univariate time series.
## Installation
To install the latest version of `auto-period-finder`, simply run:
```shell
pip install auto-period-finder
```
## Example
Start by loading a timeseries dataset with a frequency. We can use `co2` emissions sample dataset from `statsmodels`
```python
from statsmodels.datasets import co2
data = co2.load().data
```
You can resample the data to whatever frequency you want.
```python
data = data.resample("ME").mean().ffill()
```
Use `AutoPeriodFinder` to find the list of seasonality periods based on ACF.
```python
from auto_period_finder import AutoPeriodFinder
period_finder = AutoPeriodFinder(data)
periods = period_finder.fit()
```
You can also find the most prominent period either ACF-wise:
```python
strongest_period_acf = period_finder.fit_find_strongest_acf()
```
or variance-wise:
```python
strongest_period_var = period_finder.fit_find_strongest_var()
```
You can learn more about calculating seasonality component through variance from [here](OTexts.com/fpp3/stlfeatures.html).
## How to Get Started
This project is built and published using [Poetry](https://python-poetry.org). To setup development environment for this project you can follow these steps:
1. First, you need to install [Python](https://www.python.org) of one of the compatible versions indicated above.
2. Install Poetry. You can follow this [guide](https://python-poetry.org/docs/#installing-with-the-official-installer) and use their official installer.
3. Navigate to the root folder and install dependencies in a virtual environment:
```shell
poetry install
```
4. If everything worked properly, you should have `auto-period-finder-geinoPPi-py3.10` environment activated. You can verify this by running:
```shell
poetry env list
```
5. You can run tests using the command:
```shell
poetry run pytest
```
6. To export the list detailed list of dependencies, run the following command:
```shell
poetry self add poetry-plugin-export
poetry export --output requirements.txt
```
## ACF-Based Seasonality Period Detection Explained
An easy and quick way to find seasonality periods of a univariate time series is to check its autocorrelation function (ACF) and look for specific charecteristics in lag values that we will detail in a second. You can read more information about time series ACF [here](https://otexts.com/fpp3/acf.html), but intuitively, An autocorrelation coefficient $r_k$ measures the the linear relationship between $k$-lagged values of a given time series. In simpler terms, $r_k$ measures how similar/dissimilar time series values that $k$-length apart from each other. The set of $r_k$ values for each lag $k$ makes ACF. Equipped with this information, I developed a package for finding time series seasonality periods automatically using ACF information.
Simply put, given a univariate time series $T$, the algorithm finds, iteratively, lag values $k$ such that:
1. $1 \lt k \leq \frac{\lvert T \rvert}{2}$
2. Autocorrelation coefficients $r_q$ are local maxima where $q \in \{k, 2k, 3k, ...\}$
3. $\forall p \in P, \forall n \in \mathbb{N}, k \neq n \times p$, where $P$ is the list of already found periods.
The list of such $k$ values constitute the set of found seasonality periods $P$. To understand this further, consider this hypothetical time series of hourly frequency that has clear weekly seasonality below
[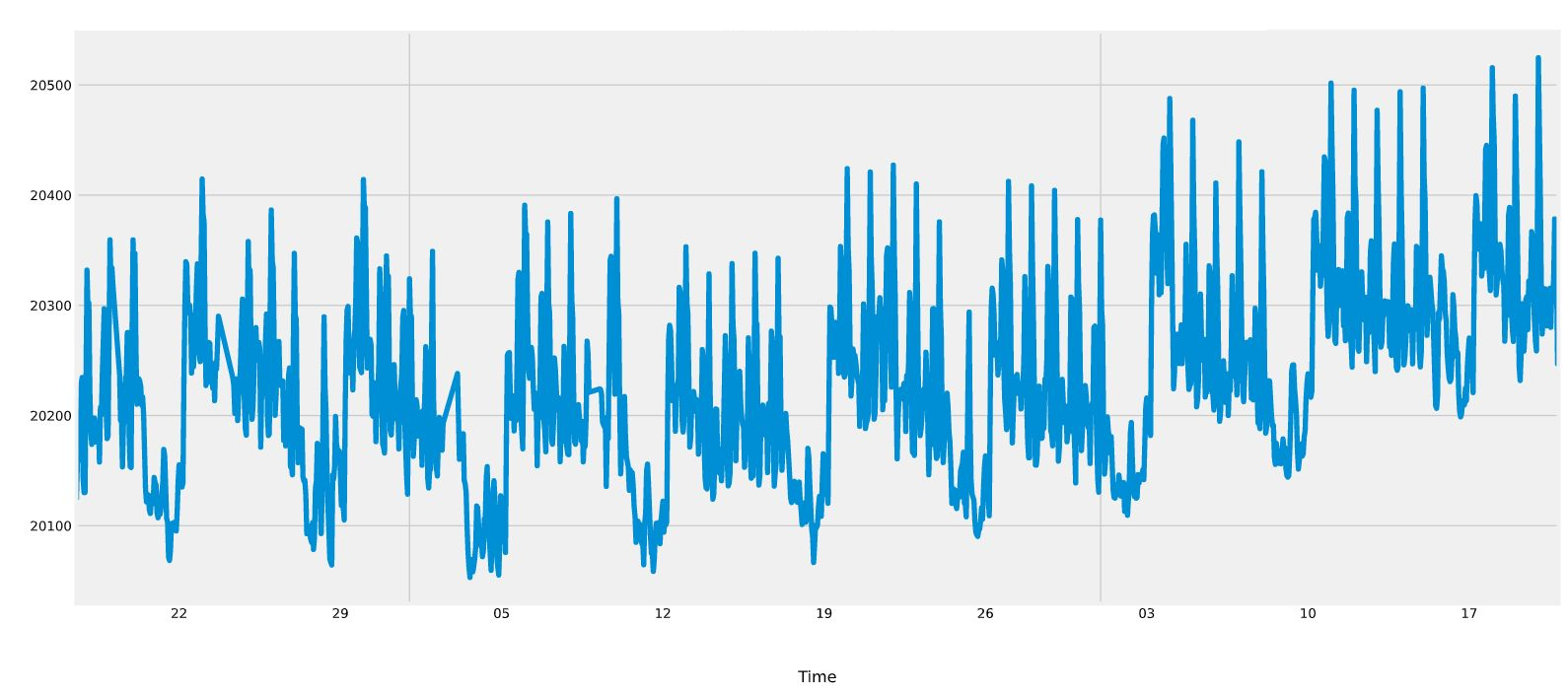](https://raw.githubusercontent.com/iskandergaba/auto-period-finder/master/assets/images/timeseries.png)
Now let's look at the corresponding ACF for the time series above:
[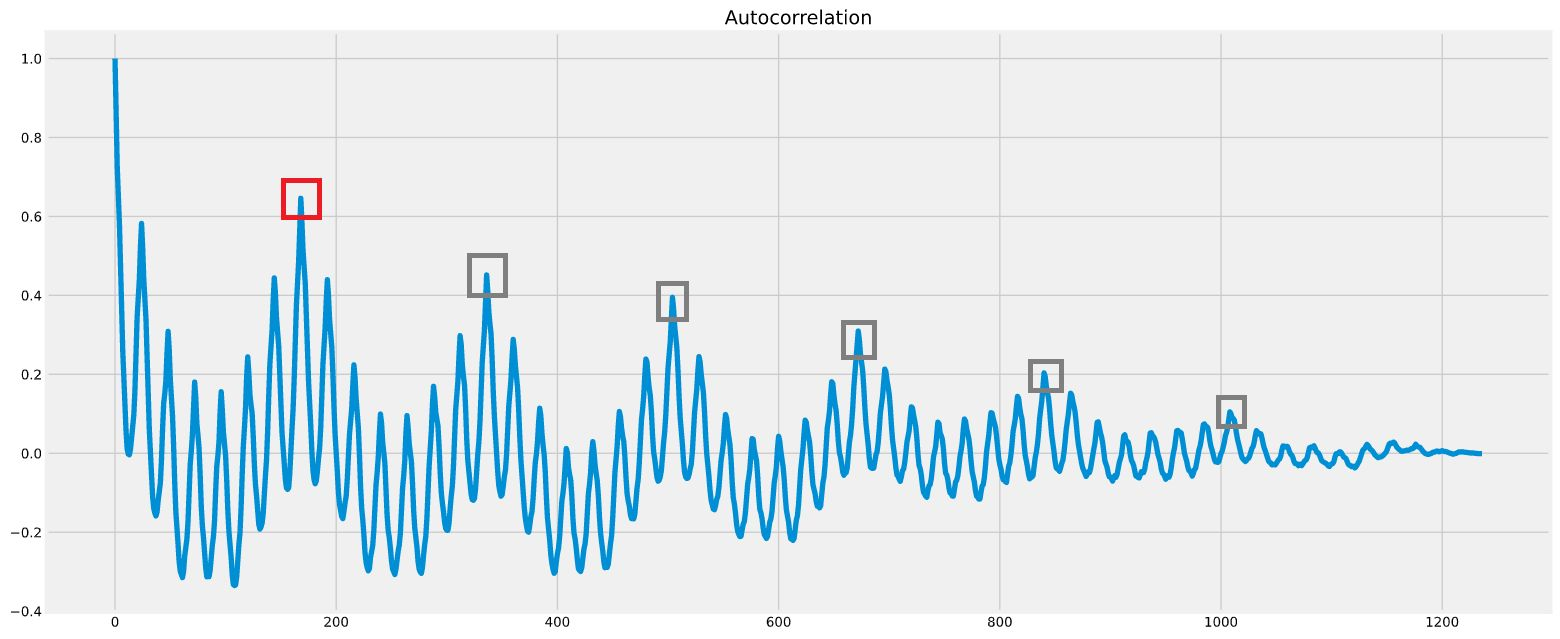](https://raw.githubusercontent.com/iskandergaba/auto-period-finder/master/assets/images/acf.png)
You can see that the autocorrelation coefficient for lag value 168 hours (i.e. one week) is a local maximum (red-border square). Similarly, autocorrelation coefficient for lag values that are multiples of 168 (gray-border squares). We can therefore conclude that this time series has a weekly seasonality period.
### Notes
- The first condition is needed because a seasonality period cannot neither be 1 (a trivial case), nor greater than half the length of the target time series (by definition, a seasonality has to manifest itself at least twice in a given time series).
- The third condition favors eliminating redundant seasonality periods that are multiples of each others. The algorithm does allow, however, finding seasonality periods that divide already found seasonality periods.
- The periods detection uses `argmax` on the ACF to select seasonality period candidates before checking they satisfy the conditions discussed above. Therefore, the list of seasonality periods are returned in the descending order of their corresponding ACF coefficients.
## References
- [1] Hyndman, R.J., & Athanasopoulos, G. (2021) Forecasting: principles and practice, 3rd edition, OTexts: Melbourne, Australia. [OTexts.com/fpp3](https://otexts.com/fpp3). Accessed on 12-25-2023.
Raw data
{
"_id": null,
"home_page": "https://github.com/iskandergaba/auto-period-finder",
"name": "auto-period-finder",
"maintainer": null,
"docs_url": null,
"requires_python": "<4.0,>=3.10",
"maintainer_email": null,
"keywords": "time, series, forecast, analysis, seasonality, trend, decomposition",
"author": "Iskander Gaba",
"author_email": "iskander@hey.com",
"download_url": "https://files.pythonhosted.org/packages/d8/a7/fb9de46970cdce39370422745e0ac1b144fe3dea12006e448edb08010b11/auto_period_finder-0.0.11.tar.gz",
"platform": null,
"description": "# `auto-period-finder`\n[](https://pypi.org/project/auto-period-finder/)\n\n\n\n## About `auto-period-finder`\n`auto-period-finder` is an autocorrelation function (ACF) based seasonality periods automatic finder for univariate time series.\n\n## Installation\nTo install the latest version of `auto-period-finder`, simply run:\n\n```shell\npip install auto-period-finder\n```\n\n## Example\nStart by loading a timeseries dataset with a frequency. We can use `co2` emissions sample dataset from `statsmodels`\n```python\nfrom statsmodels.datasets import co2\ndata = co2.load().data\n```\n\nYou can resample the data to whatever frequency you want.\n\n```python\ndata = data.resample(\"ME\").mean().ffill()\n```\n\nUse `AutoPeriodFinder` to find the list of seasonality periods based on ACF.\n```python\nfrom auto_period_finder import AutoPeriodFinder\nperiod_finder = AutoPeriodFinder(data)\nperiods = period_finder.fit()\n```\n\nYou can also find the most prominent period either ACF-wise:\n```python\nstrongest_period_acf = period_finder.fit_find_strongest_acf()\n```\n\nor variance-wise:\n```python\nstrongest_period_var = period_finder.fit_find_strongest_var()\n```\nYou can learn more about calculating seasonality component through variance from [here](OTexts.com/fpp3/stlfeatures.html).\n\n\n## How to Get Started\nThis project is built and published using [Poetry](https://python-poetry.org). To setup development environment for this project you can follow these steps:\n\n1. First, you need to install [Python](https://www.python.org) of one of the compatible versions indicated above.\n2. Install Poetry. You can follow this [guide](https://python-poetry.org/docs/#installing-with-the-official-installer) and use their official installer.\n3. Navigate to the root folder and install dependencies in a virtual environment:\n```shell\npoetry install\n```\n4. If everything worked properly, you should have `auto-period-finder-geinoPPi-py3.10` environment activated. You can verify this by running:\n```shell\npoetry env list\n```\n5. You can run tests using the command:\n```shell\npoetry run pytest\n```\n6. To export the list detailed list of dependencies, run the following command:\n```shell\npoetry self add poetry-plugin-export\npoetry export --output requirements.txt\n```\n\n## ACF-Based Seasonality Period Detection Explained\nAn easy and quick way to find seasonality periods of a univariate time series is to check its autocorrelation function (ACF) and look for specific charecteristics in lag values that we will detail in a second. You can read more information about time series ACF [here](https://otexts.com/fpp3/acf.html), but intuitively, An autocorrelation coefficient $r_k$ measures the the linear relationship between $k$-lagged values of a given time series. In simpler terms, $r_k$ measures how similar/dissimilar time series values that $k$-length apart from each other. The set of $r_k$ values for each lag $k$ makes ACF. Equipped with this information, I developed a package for finding time series seasonality periods automatically using ACF information.\n\nSimply put, given a univariate time series $T$, the algorithm finds, iteratively, lag values $k$ such that:\n1. $1 \\lt k \\leq \\frac{\\lvert T \\rvert}{2}$\n2. Autocorrelation coefficients $r_q$ are local maxima where $q \\in \\{k, 2k, 3k, ...\\}$\n3. $\\forall p \\in P, \\forall n \\in \\mathbb{N}, k \\neq n \\times p$, where $P$ is the list of already found periods.\n\nThe list of such $k$ values constitute the set of found seasonality periods $P$. To understand this further, consider this hypothetical time series of hourly frequency that has clear weekly seasonality below\n\n[](https://raw.githubusercontent.com/iskandergaba/auto-period-finder/master/assets/images/timeseries.png)\n\nNow let's look at the corresponding ACF for the time series above:\n\n[](https://raw.githubusercontent.com/iskandergaba/auto-period-finder/master/assets/images/acf.png)\n\nYou can see that the autocorrelation coefficient for lag value 168 hours (i.e. one week) is a local maximum (red-border square). Similarly, autocorrelation coefficient for lag values that are multiples of 168 (gray-border squares). We can therefore conclude that this time series has a weekly seasonality period.\n\n### Notes\n- The first condition is needed because a seasonality period cannot neither be 1 (a trivial case), nor greater than half the length of the target time series (by definition, a seasonality has to manifest itself at least twice in a given time series).\n- The third condition favors eliminating redundant seasonality periods that are multiples of each others. The algorithm does allow, however, finding seasonality periods that divide already found seasonality periods.\n- The periods detection uses `argmax` on the ACF to select seasonality period candidates before checking they satisfy the conditions discussed above. Therefore, the list of seasonality periods are returned in the descending order of their corresponding ACF coefficients.\n\n## References\n- [1] Hyndman, R.J., & Athanasopoulos, G. (2021) Forecasting: principles and practice, 3rd edition, OTexts: Melbourne, Australia. [OTexts.com/fpp3](https://otexts.com/fpp3). Accessed on 12-25-2023.\n",
"bugtrack_url": null,
"license": "MIT",
"summary": "An autocorrelation function-based seasonality periods automatic finder for univariate time series.",
"version": "0.0.11",
"project_urls": {
"Homepage": "https://github.com/iskandergaba/auto-period-finder",
"Repository": "https://github.com/iskandergaba/auto-period-finder"
},
"split_keywords": [
"time",
" series",
" forecast",
" analysis",
" seasonality",
" trend",
" decomposition"
],
"urls": [
{
"comment_text": "",
"digests": {
"blake2b_256": "e584d2f06bd12cc8a1d9989632b8a3002b0b99ab1b98e6b1120ad5a9d52bad7b",
"md5": "64a63cf410bcff636cf28046d0759395",
"sha256": "d18bec069485ee00ea312cfaebc80b0278ef2da3b084fd08c70ebcfdea7abb41"
},
"downloads": -1,
"filename": "auto_period_finder-0.0.11-py3-none-any.whl",
"has_sig": false,
"md5_digest": "64a63cf410bcff636cf28046d0759395",
"packagetype": "bdist_wheel",
"python_version": "py3",
"requires_python": "<4.0,>=3.10",
"size": 7651,
"upload_time": "2024-04-08T00:31:54",
"upload_time_iso_8601": "2024-04-08T00:31:54.424267Z",
"url": "https://files.pythonhosted.org/packages/e5/84/d2f06bd12cc8a1d9989632b8a3002b0b99ab1b98e6b1120ad5a9d52bad7b/auto_period_finder-0.0.11-py3-none-any.whl",
"yanked": false,
"yanked_reason": null
},
{
"comment_text": "",
"digests": {
"blake2b_256": "d8a7fb9de46970cdce39370422745e0ac1b144fe3dea12006e448edb08010b11",
"md5": "4cab6a0ea43778957059e336fdba715a",
"sha256": "e96cef737bfae3bbfb292724daaa74d905368488c3d1b6da208a0c8b5197e100"
},
"downloads": -1,
"filename": "auto_period_finder-0.0.11.tar.gz",
"has_sig": false,
"md5_digest": "4cab6a0ea43778957059e336fdba715a",
"packagetype": "sdist",
"python_version": "source",
"requires_python": "<4.0,>=3.10",
"size": 6557,
"upload_time": "2024-04-08T00:31:56",
"upload_time_iso_8601": "2024-04-08T00:31:56.174044Z",
"url": "https://files.pythonhosted.org/packages/d8/a7/fb9de46970cdce39370422745e0ac1b144fe3dea12006e448edb08010b11/auto_period_finder-0.0.11.tar.gz",
"yanked": false,
"yanked_reason": null
}
],
"upload_time": "2024-04-08 00:31:56",
"github": true,
"gitlab": false,
"bitbucket": false,
"codeberg": false,
"github_user": "iskandergaba",
"github_project": "auto-period-finder",
"travis_ci": false,
"coveralls": false,
"github_actions": true,
"requirements": [],
"lcname": "auto-period-finder"
}
