| Name | cbfpy JSON |
| Version |
0.0.1
 JSON
JSON |
| download |
| home_page | None |
| Summary | Control Barrier Functions in Python |
| upload_time | 2024-12-10 06:25:42 |
| maintainer | None |
| docs_url | None |
| author | None |
| requires_python | None |
| license | None |
| keywords |
control
barrier
function
cbf
jax
|
| VCS |
 |
| bugtrack_url |
|
| requirements |
No requirements were recorded.
|
| Travis-CI |
No Travis.
|
| coveralls test coverage |
No coveralls.
|
# CBFpy: Control Barrier Functions in Python and Jax
CBFpy is an easy-to-use and high-performance framework for constructing and solving Control Barrier Functions (CBFs) and Control Lyapunov Functions (CLFs), using [Jax](https://github.com/google/jax) for:
- Just-in-time compilation
- Accelerated linear algebra operations with [XLA](https://openxla.org/xla)
- Automatic differentiation
For API reference, see the following [documentation](https://danielpmorton.github.io/cbfpy)
If you use CBFpy in your research, please use the following citation:
```
@software{Morton_CBFpy_2024,
author = {Morton, Daniel},
license = {MIT},
title = {{CBFpy: Control Barrier Functions in Python and Jax}},
url = {https://github.com/danielpmorton/cbfpy},
version = {0.0.1},
month = Dec,
year = {2024}
}
```
## Installation
### From PyPI
```
pip install cbfpy
```
### From source
A virtual environment is optional, but highly recommended. For `pyenv` installation instructions, see [here](https://danielpmorton.github.io/cbfpy/pyenv).
```
git clone https://github.com/danielpmorton/cbfpy
cd cbfpy
pip install -e ".[examples]"
```
The `[examples]` tag installs all of the required packages for development and running the examples. The pure `cbfpy` functionality does not require these extra packages though. If you want to contribute to the repo, you can also include the `[dev]` dependencies.
If you are working on Apple silicon and have issues installing Jax, the following threads may be useful: [[1]](https://stackoverflow.com/questions/68327863/importing-jax-fails-on-mac-with-m1-chip), [[2]](https://github.com/jax-ml/jax/issues/5501#issuecomment-955590288)
## Usage:
#### Example: A point-mass robot in 1D with an applied force and a positional barrier
For this problem, the state $z$ is defined as the position and velocity of the robot,
$$z = [x, \dot{x}]$$
So, the state derivative $\dot{z}$ is therefore
$$\dot{z} = [\dot{x}, \ddot{x}]$$
And the control input is the applied force in the $x$ direction:
$$u = F_{x}$$
The dynamics can be expressed as follows (with $m$ denoting the robot's mass):
$$\dot{z} = \begin{bmatrix}0 & 1 \\
0 & 0
\end{bmatrix}z +
\begin{bmatrix}0 \\
1/m
\end{bmatrix} u$$
This is a control affine system, since the dynamics can be expressed as
$$\dot{z} = f(z) + g(z) u$$
If the robot is controlled by some nominal (unsafe) controller, we may want to guarantee that it remains in some safe region. If we define $X_{safe} \in [x_{min}, \infty]$, we can construct a (relative-degree-2, zeroing) barrier $h$ where $h(z) \geq 0$ for any $z$ in the safe set:
$$h(z) = x - x_{min}$$
### In Code
We'll first define our problem (dynamics, barrier, and any additional parameters) in a `CBFConfig`-derived class.
We use [Jax](https://github.com/google/jax) for fast compilation of the problem. Jax can be tricky to learn at first, but luckily `cbfpy` just requires formulating your functions in `jax.numpy` which has the same familiar interface as `numpy`. These should be pure functions without side effects (for instance, modifying a class variable in `self`).
Additional tuning parameters/functions can be found in the `CBFConfig` documentation.
```python
import jax.numpy as jnp
from cbfpy import CBF, CBFConfig
# Create a config class for your problem inheriting from the CBFConfig class
class MyCBFConfig(CBFConfig):
def __init__(self):
super().__init__(
# Define the state and control dimensions
n = 2, # [x, x_dot]
m = 1, # [F_x]
# Define control limits (if desired)
u_min = None,
u_max = None,
)
# Define the control-affine dynamics functions `f` and `g` for your system
def f(self, z):
A = jnp.array([[0.0, 1.0], [0.0, 0.0]])
return A @ z
def g(self, z):
mass = 1.0
B = jnp.array([[0.0], [1.0 / mass]])
return B
# Define the barrier function `h`
# The *relative degree* of this system is 2, so, we'll use the h_2 method
def h_2(self, z):
x_min = 1.0
x = z[0]
return jnp.array([x - x_min])
```
We can then construct the CBF from our config and use it in our control loop as follows.
```python
config = MyCBFConfig()
cbf = CBF.from_config(config)
# Pseudocode
while True:
z = get_state()
z_des = get_desired_state()
u_nom = nominal_controller(z, z_des)
u = cbf.safety_filter(z, u_nom)
apply_control(u)
step()
```
## Examples
These can be found in the `examples` folder [here](https://github.com/danielpmorton/cbfpy/tree/main/cbfpy/examples)
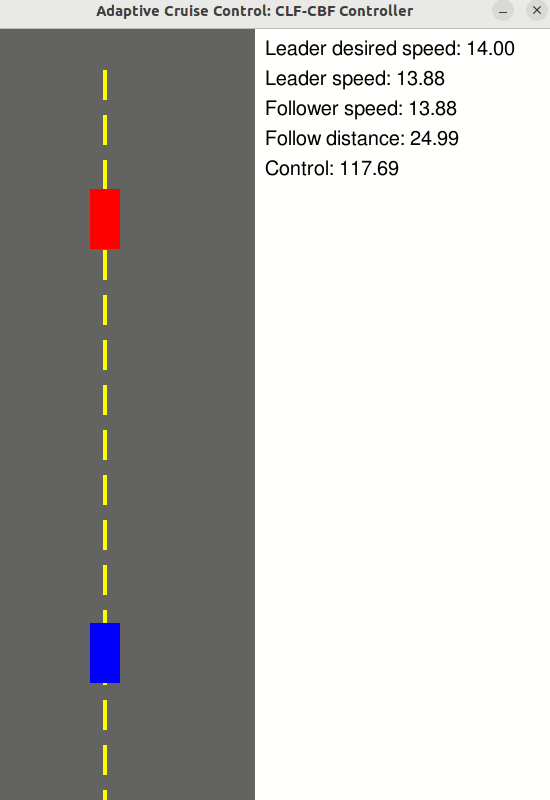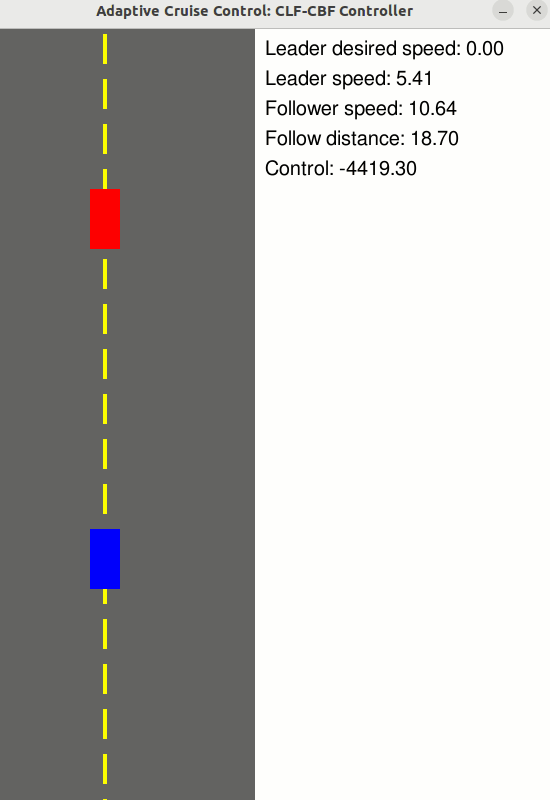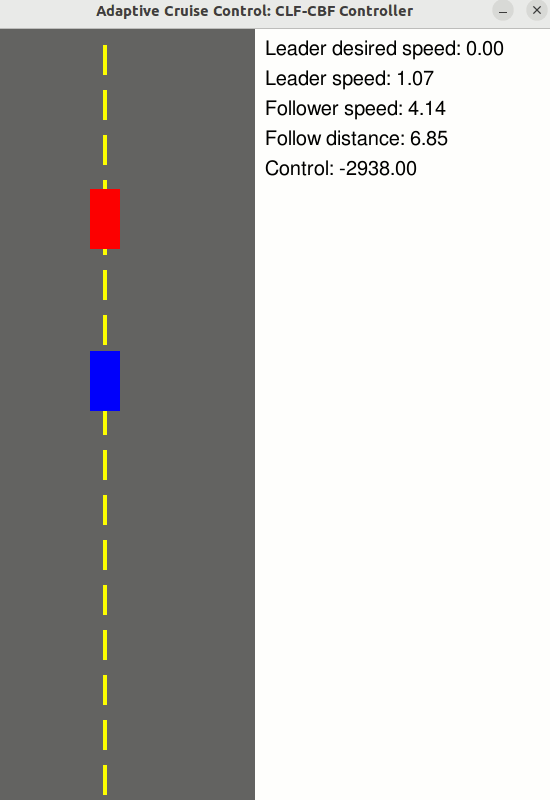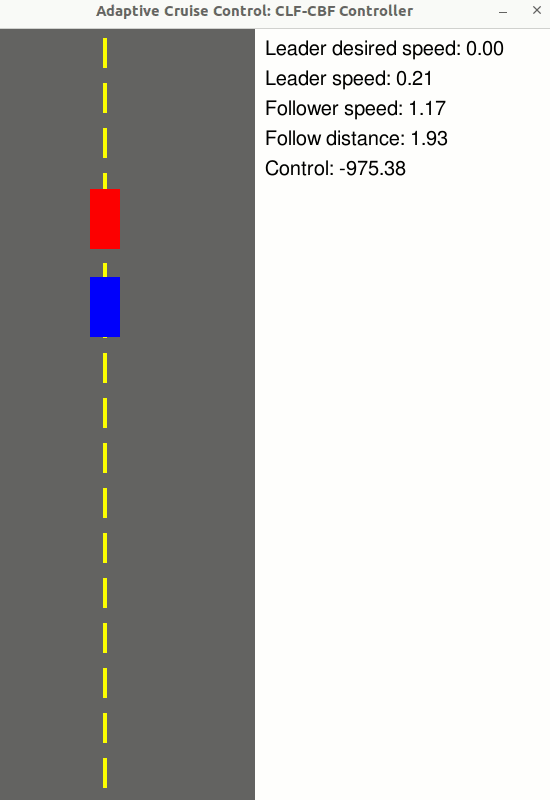
### [Adaptive Cruise Control](https://github.com/danielpmorton/cbfpy/blob/main/cbfpy/examples/adaptive_cruise_control_demo.py)
Use a CLF-CBF to maintain a safe follow distance to the vehicle in front, while tracking a desired velocity
- State: z = [Follower velocity, Leader velocity, Follow distance] (n = 3)
- Control: u = [Follower wheel force] (m = 1)
- Relative degree: 1
### [Point Robot Safe-Set Containment](https://github.com/danielpmorton/cbfpy/blob/main/cbfpy/examples/point_robot_demo.py)
Use a CBF to enforce that a point robot stays within a safe box, while a PD controller attempts to reduce the distance to a target position
- State: z = [Position, Velocity] (n = 6)
- Control: u = [Force] (m = 3)
- Relative degree: 2

### [Point Robot Obstacle Avoidance](https://github.com/danielpmorton/cbfpy/blob/main/cbfpy/examples/point_robot_obstacle_demo.py)
Use a CBF to keep a point robot inside a safe box, while avoiding a moving obstacle. The nominal PD controller attempts to keep the robot at the origin.
- State: z = [Position, Velocity] (n = 6)
- Control: u = [Force] (m = 3)
- Relative degree: 1 + 2 (1 for obstacle avoidance, 2 for safe set containment)
- Additional data: The state of the obstacle (position and velocity)

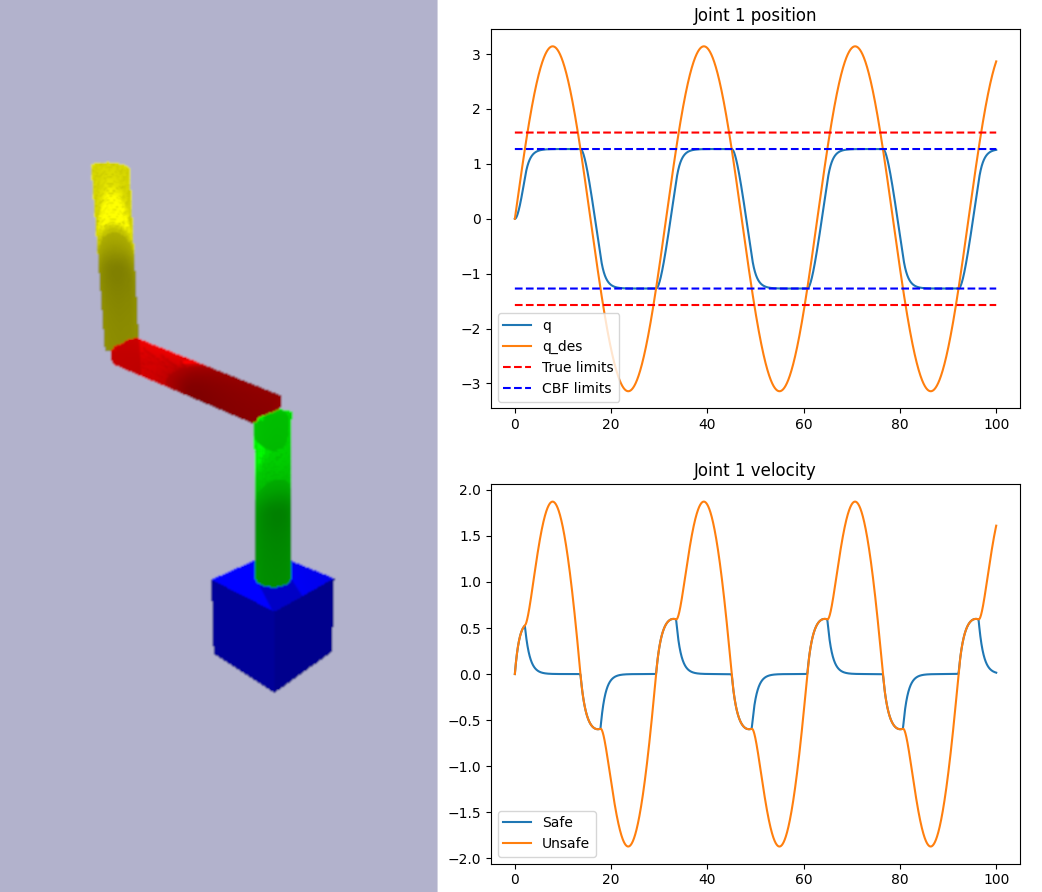
### [Manipulator Joint Limit Avoidance](https://github.com/danielpmorton/cbfpy/blob/main/cbfpy/examples/joint_limits_demo.py)
Use a CBF to keep a manipulator operating within its joint limits, even if a nominal joint trajectory is unsafe.
- State: z = [Joint angles] (n = 3)
- Control: u = [Joint velocities] (m = 3)
- Relative degree: 1
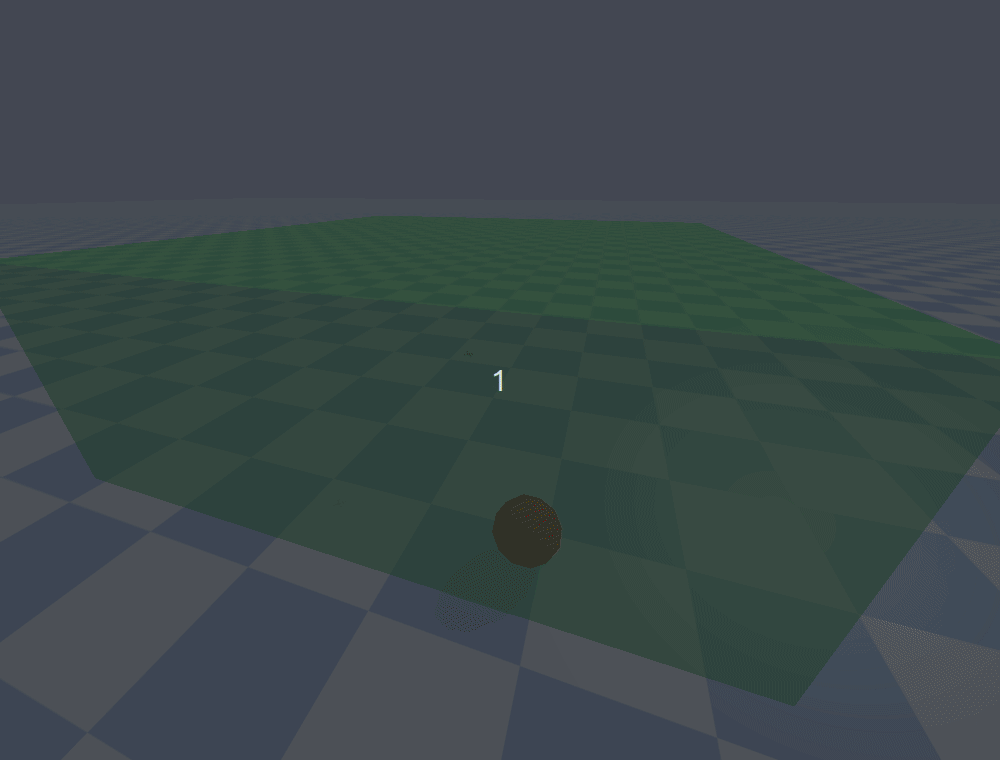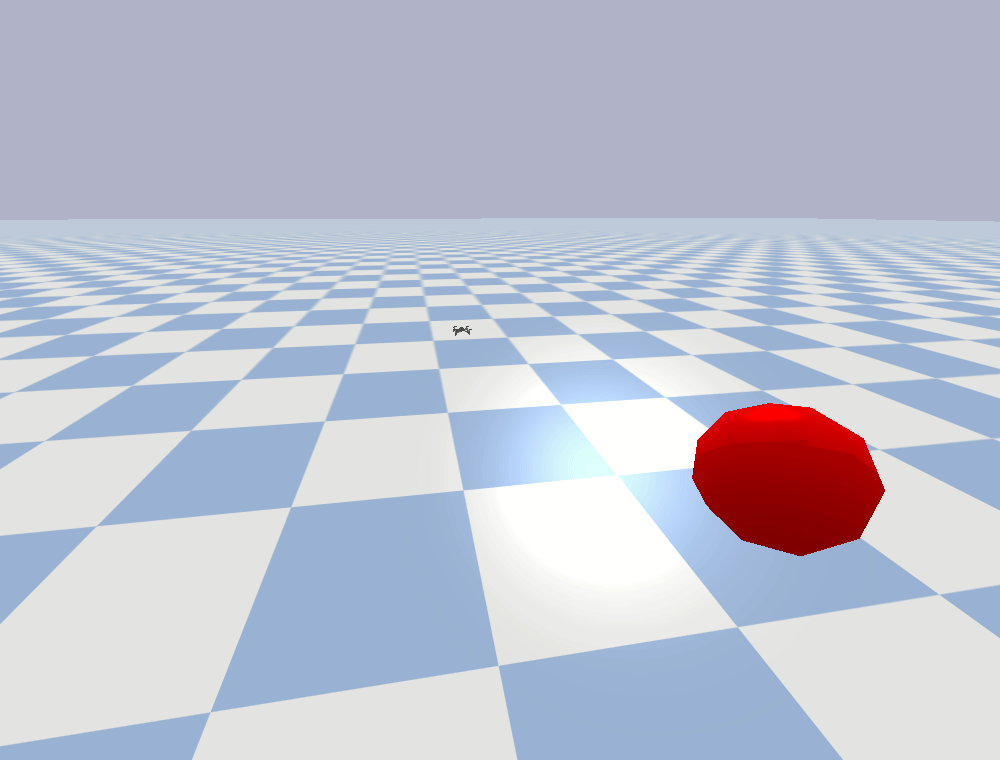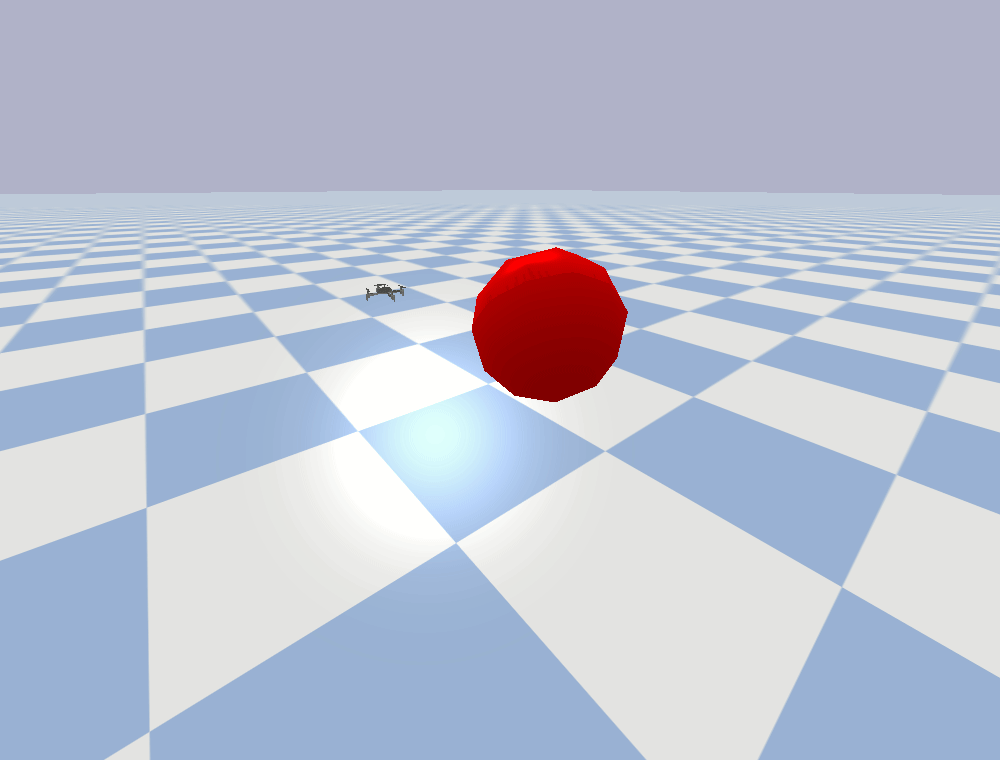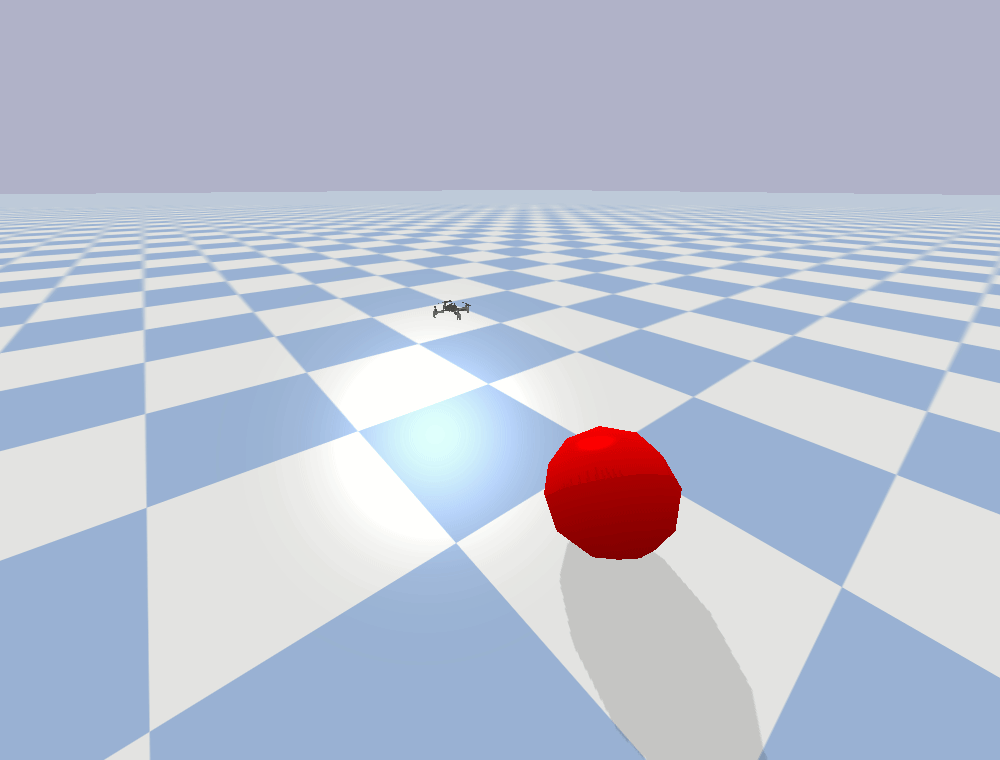
### [Drone Obstacle Avoidance](https://github.com/danielpmorton/cbfpy/blob/main/cbfpy/examples/drone_demo.py)
Use a CBF to keep a drone inside a safe box, while avoiding a moving obstacle. This is similar to the "point robot obstacle avoidance" demo, but with slightly different dynamics.
- State: z = [Position, Velocity] (n = 6)
- Control: u = [Velocity] (m = 3)
- Relative degree: 1
- Additional data: The state of the obstacle (position and velocity)
This is the same CBF which was used in the ["Drone Fencing" demo](https://danielpmorton.github.io/drone_fencing/) at the Stanford Robotics center.
Raw data
{
"_id": null,
"home_page": null,
"name": "cbfpy",
"maintainer": null,
"docs_url": null,
"requires_python": null,
"maintainer_email": null,
"keywords": "control, barrier, function, CBF, Jax",
"author": null,
"author_email": "Daniel Morton <danielpmorton@gmail.com>",
"download_url": "https://files.pythonhosted.org/packages/f1/8d/46b83f4a681e057ebaa9c0b82f305800d285d7b714ca004250155b773495/cbfpy-0.0.1.tar.gz",
"platform": null,
"description": "# CBFpy: Control Barrier Functions in Python and Jax\n\nCBFpy is an easy-to-use and high-performance framework for constructing and solving Control Barrier Functions (CBFs) and Control Lyapunov Functions (CLFs), using [Jax](https://github.com/google/jax) for:\n\n- Just-in-time compilation\n- Accelerated linear algebra operations with [XLA](https://openxla.org/xla)\n- Automatic differentiation\n\nFor API reference, see the following [documentation](https://danielpmorton.github.io/cbfpy)\n\nIf you use CBFpy in your research, please use the following citation:\n\n```\n@software{Morton_CBFpy_2024,\n author = {Morton, Daniel},\n license = {MIT},\n title = {{CBFpy: Control Barrier Functions in Python and Jax}},\n url = {https://github.com/danielpmorton/cbfpy},\n version = {0.0.1},\n month = Dec,\n year = {2024}\n}\n```\n\n## Installation \n\n### From PyPI\n\n```\npip install cbfpy\n```\n\n### From source\n\nA virtual environment is optional, but highly recommended. For `pyenv` installation instructions, see [here](https://danielpmorton.github.io/cbfpy/pyenv).\n\n```\ngit clone https://github.com/danielpmorton/cbfpy\ncd cbfpy\npip install -e \".[examples]\"\n```\nThe `[examples]` tag installs all of the required packages for development and running the examples. The pure `cbfpy` functionality does not require these extra packages though. If you want to contribute to the repo, you can also include the `[dev]` dependencies.\n\nIf you are working on Apple silicon and have issues installing Jax, the following threads may be useful: [[1]](https://stackoverflow.com/questions/68327863/importing-jax-fails-on-mac-with-m1-chip), [[2]](https://github.com/jax-ml/jax/issues/5501#issuecomment-955590288)\n\n## Usage:\n\n#### Example: A point-mass robot in 1D with an applied force and a positional barrier\n\nFor this problem, the state $z$ is defined as the position and velocity of the robot,\n\n$$z = [x, \\dot{x}]$$ \n\nSo, the state derivative $\\dot{z}$ is therefore\n\n$$\\dot{z} = [\\dot{x}, \\ddot{x}]$$ \n\nAnd the control input is the applied force in the $x$ direction:\n\n$$u = F_{x}$$\n\nThe dynamics can be expressed as follows (with $m$ denoting the robot's mass):\n\n$$\\dot{z} = \\begin{bmatrix}0 & 1 \\\\\n 0 & 0\n \\end{bmatrix}z + \n \\begin{bmatrix}0 \\\\\n 1/m\n \\end{bmatrix} u$$\n\nThis is a control affine system, since the dynamics can be expressed as \n\n$$\\dot{z} = f(z) + g(z) u$$\n\nIf the robot is controlled by some nominal (unsafe) controller, we may want to guarantee that it remains in some safe region. If we define $X_{safe} \\in [x_{min}, \\infty]$, we can construct a (relative-degree-2, zeroing) barrier $h$ where $h(z) \\geq 0$ for any $z$ in the safe set:\n\n$$h(z) = x - x_{min}$$\n\n### In Code\n\nWe'll first define our problem (dynamics, barrier, and any additional parameters) in a `CBFConfig`-derived class. \n\nWe use [Jax](https://github.com/google/jax) for fast compilation of the problem. Jax can be tricky to learn at first, but luckily `cbfpy` just requires formulating your functions in `jax.numpy` which has the same familiar interface as `numpy`. These should be pure functions without side effects (for instance, modifying a class variable in `self`).\n\nAdditional tuning parameters/functions can be found in the `CBFConfig` documentation. \n\n```python\nimport jax.numpy as jnp\nfrom cbfpy import CBF, CBFConfig\n\n# Create a config class for your problem inheriting from the CBFConfig class\nclass MyCBFConfig(CBFConfig):\n def __init__(self):\n super().__init__(\n # Define the state and control dimensions\n n = 2, # [x, x_dot]\n m = 1, # [F_x]\n # Define control limits (if desired)\n u_min = None,\n u_max = None,\n )\n\n # Define the control-affine dynamics functions `f` and `g` for your system\n def f(self, z):\n A = jnp.array([[0.0, 1.0], [0.0, 0.0]])\n return A @ z\n\n def g(self, z):\n mass = 1.0\n B = jnp.array([[0.0], [1.0 / mass]])\n return B\n\n # Define the barrier function `h`\n # The *relative degree* of this system is 2, so, we'll use the h_2 method\n def h_2(self, z):\n x_min = 1.0\n x = z[0]\n return jnp.array([x - x_min])\n```\nWe can then construct the CBF from our config and use it in our control loop as follows.\n```python\nconfig = MyCBFConfig()\ncbf = CBF.from_config(config)\n\n# Pseudocode\nwhile True:\n z = get_state()\n z_des = get_desired_state()\n u_nom = nominal_controller(z, z_des)\n u = cbf.safety_filter(z, u_nom)\n apply_control(u)\n step() \n```\n\n## Examples\n\nThese can be found in the `examples` folder [here](https://github.com/danielpmorton/cbfpy/tree/main/cbfpy/examples)\n\n### [Adaptive Cruise Control](https://github.com/danielpmorton/cbfpy/blob/main/cbfpy/examples/adaptive_cruise_control_demo.py)\n\nUse a CLF-CBF to maintain a safe follow distance to the vehicle in front, while tracking a desired velocity\n\n- State: z = [Follower velocity, Leader velocity, Follow distance] (n = 3)\n- Control: u = [Follower wheel force] (m = 1)\n- Relative degree: 1\n\n\n\n### [Point Robot Safe-Set Containment](https://github.com/danielpmorton/cbfpy/blob/main/cbfpy/examples/point_robot_demo.py)\n\nUse a CBF to enforce that a point robot stays within a safe box, while a PD controller attempts to reduce the distance to a target position\n\n- State: z = [Position, Velocity] (n = 6)\n- Control: u = [Force] (m = 3)\n- Relative degree: 2\n\n\n\n### [Point Robot Obstacle Avoidance](https://github.com/danielpmorton/cbfpy/blob/main/cbfpy/examples/point_robot_obstacle_demo.py)\n\nUse a CBF to keep a point robot inside a safe box, while avoiding a moving obstacle. The nominal PD controller attempts to keep the robot at the origin.\n\n- State: z = [Position, Velocity] (n = 6)\n- Control: u = [Force] (m = 3)\n- Relative degree: 1 + 2 (1 for obstacle avoidance, 2 for safe set containment)\n- Additional data: The state of the obstacle (position and velocity)\n\n\n\n### [Manipulator Joint Limit Avoidance](https://github.com/danielpmorton/cbfpy/blob/main/cbfpy/examples/joint_limits_demo.py)\n\nUse a CBF to keep a manipulator operating within its joint limits, even if a nominal joint trajectory is unsafe. \n\n- State: z = [Joint angles] (n = 3)\n- Control: u = [Joint velocities] (m = 3)\n- Relative degree: 1\n\n\n\n### [Drone Obstacle Avoidance](https://github.com/danielpmorton/cbfpy/blob/main/cbfpy/examples/drone_demo.py)\n\nUse a CBF to keep a drone inside a safe box, while avoiding a moving obstacle. This is similar to the \"point robot obstacle avoidance\" demo, but with slightly different dynamics.\n\n- State: z = [Position, Velocity] (n = 6)\n- Control: u = [Velocity] (m = 3)\n- Relative degree: 1\n- Additional data: The state of the obstacle (position and velocity)\n\nThis is the same CBF which was used in the [\"Drone Fencing\" demo](https://danielpmorton.github.io/drone_fencing/) at the Stanford Robotics center.\n\n\n",
"bugtrack_url": null,
"license": null,
"summary": "Control Barrier Functions in Python",
"version": "0.0.1",
"project_urls": {
"Documentation": "https://danielpmorton.github.io/cbfpy/",
"Repository": "https://github.com/danielpmorton/cbfpy/"
},
"split_keywords": [
"control",
" barrier",
" function",
" cbf",
" jax"
],
"urls": [
{
"comment_text": "",
"digests": {
"blake2b_256": "6b649c64b48bb5afdea351653a2eef5c105abf51ec8f4c9424c6650153026a6a",
"md5": "7ae295bef45375980abf0b46300c3961",
"sha256": "4c10ceb9f8614c4fd400b43a907624090b11e4c2c3041ddd5c427d128eda7220"
},
"downloads": -1,
"filename": "cbfpy-0.0.1-py3-none-any.whl",
"has_sig": false,
"md5_digest": "7ae295bef45375980abf0b46300c3961",
"packagetype": "bdist_wheel",
"python_version": "py3",
"requires_python": null,
"size": 46919,
"upload_time": "2024-12-10T06:25:39",
"upload_time_iso_8601": "2024-12-10T06:25:39.598719Z",
"url": "https://files.pythonhosted.org/packages/6b/64/9c64b48bb5afdea351653a2eef5c105abf51ec8f4c9424c6650153026a6a/cbfpy-0.0.1-py3-none-any.whl",
"yanked": false,
"yanked_reason": null
},
{
"comment_text": "",
"digests": {
"blake2b_256": "f18d46b83f4a681e057ebaa9c0b82f305800d285d7b714ca004250155b773495",
"md5": "cd4ee373c9f663de7b0641bb361f395d",
"sha256": "05c4795467d4de60396e61c1661068c7ded1ec54e08b708becd3596f60889a65"
},
"downloads": -1,
"filename": "cbfpy-0.0.1.tar.gz",
"has_sig": false,
"md5_digest": "cd4ee373c9f663de7b0641bb361f395d",
"packagetype": "sdist",
"python_version": "source",
"requires_python": null,
"size": 36063,
"upload_time": "2024-12-10T06:25:42",
"upload_time_iso_8601": "2024-12-10T06:25:42.250457Z",
"url": "https://files.pythonhosted.org/packages/f1/8d/46b83f4a681e057ebaa9c0b82f305800d285d7b714ca004250155b773495/cbfpy-0.0.1.tar.gz",
"yanked": false,
"yanked_reason": null
}
],
"upload_time": "2024-12-10 06:25:42",
"github": true,
"gitlab": false,
"bitbucket": false,
"codeberg": false,
"github_user": "danielpmorton",
"github_project": "cbfpy",
"travis_ci": false,
"coveralls": false,
"github_actions": true,
"lcname": "cbfpy"
}
