# `dheapy`
`dheapy` is a pure Python implementation of $d$-ary heap data structure for priority queue applications, which can work for both max-heap and min-heap variants. The factor $d$ in $d$-ary heap is called the branching factor and it can be equal to or greater than $2$, where $d=2$ means the heap is built with a binary tree, $d=3$ with a ternary tree, $d=4$ with a quaternary tree, and so on.
The branching factor of a tree is the maximum number of children a node can have.
A $2$-ary heap or binary heap has a branching factor of $2$:
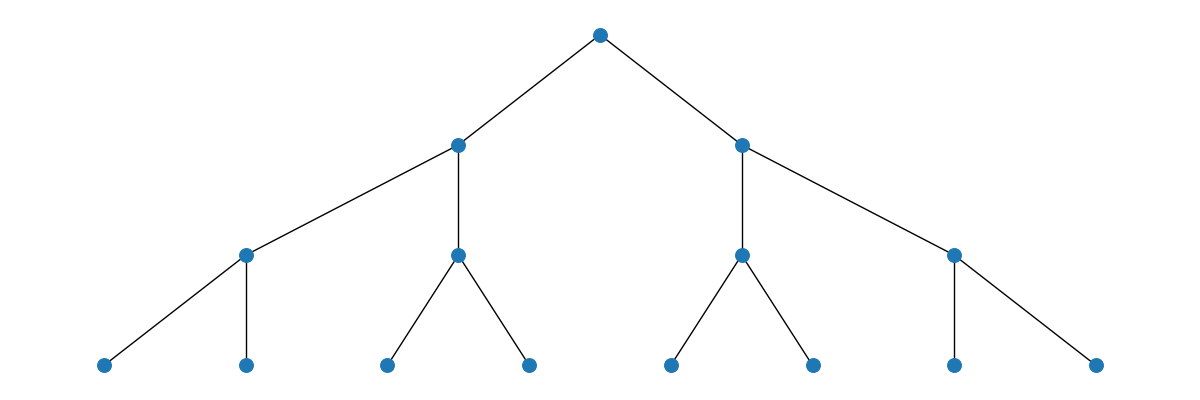
A $3$-ary heap or ternary heap has a branching factor of $3$:
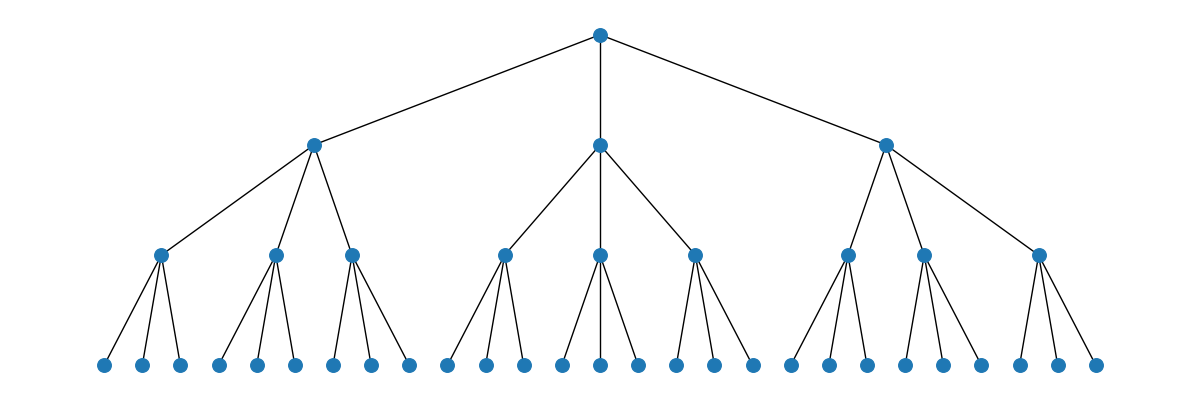
A $4$-ary heap or quaternary heap has a branching factor of $4$:
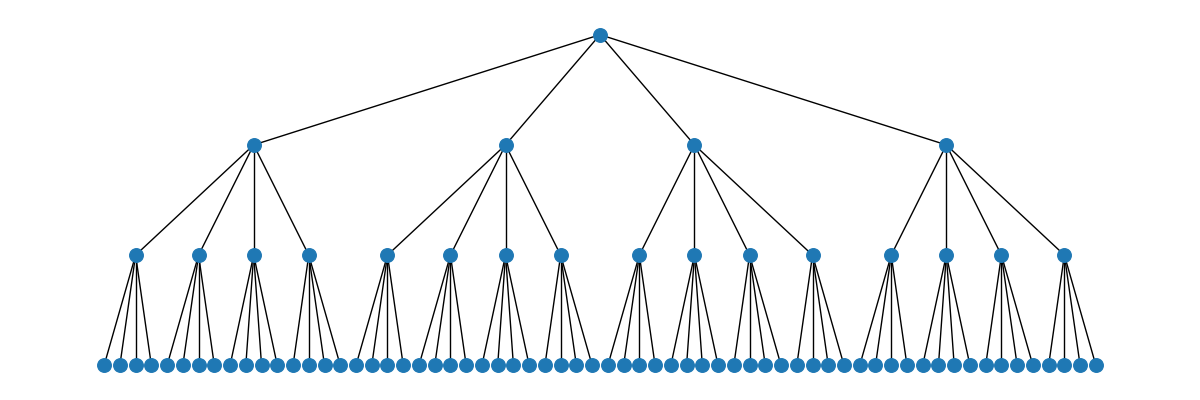
`dheapy` is array-based and adaptable, where arbitrary items can be removed, updated, and displayed on the go.
The library also comes with a sorting function that is based on the heap-sort algorithm to sort lists of tuples.
## Installation
Use the package manager [pip](https://pip.pypa.io/en/stable/) to install `dheapy`:
```
pip install dheapy
```
## Prerequisites
None.
## Usage
1. `DHeap(branching_factor=2, variant='max')`
Class to create an empty and perform priority queue operations (shown in the table below).
Parameters:
- `branching_factor`: `int`; default = `2`
- `variant`: `str`, either `'max'` or `'min'`; default = `'max'`
To import `DHeap` class:
```
from dheapy import DHeap
```
2. `heapsorted(object, branching_factor=2, variant='max')`
Function for sorting arrays that is based on the heap sort algorithm.
Parameters:
- `object`: array or iterable
- `branching_factor`: `int`; default = `2`
- `variant`: `str`, either `'max'` or `'min'`; default = `'max'`
To import `heapsorted()` function
```
from dheapy import heapsorted
```
To create an empty priority queue with branching factor 3 and min-heap variant:
```
P = DHeap(3, 'min')
```
The following are operations that can be performed with `DHeap` class:
| **Operation** | **Description** | **Object Returned** |
| ------------------------------ | -------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------- | ------------------- |
| `P.insert(k,v)` | adds a new item with priority number `k` and element/description `v` into priority queue. The priority number `k` must be positive and can be of integer or floating-point type; the priority element/description `v` can be of any type. | |
| `P.peek()` | returns the highest priority item, but without extracting/removing it from the queue. | `(k, v)` |
| `P.delete()` | removes/deletes the highest priority item from the queue. | `(k, v)` |
| `P.removeitem(k, v)` | removes an item with priority number `k` and element `v` from the queue. | `(k, v)` |
| `P.update(old_item, new_item)` | updates a pair of old item (in tuple, which consists of a priority number and its element) and replaces it with a pair of new item (in tuple, which consists of a priority number and its element). This operation can also be used to update a priority number or element only. | |
| `len(P)` | returns the number of items in priority queue `P`. | `int` |
| `is_empty(P)` | returns `True` if priority queue `P` does not contain any items. | `True` or `False` |
| `P.contains(k, v)` | returns `True` if priority queue `P` contains an item with priority number `k` with element `v`. | `True` or `False` |
| `P.show(i)` | returns the item at index `i`. | `(k, v)` |
## Performance
| **Operation** | **Time Complexity** |
| ------------------------------ | ------------------- |
| `P.insert(k,v)` | O(log n) |
| `P.peek()` | O(1) |
| `P.delete()` | O(log n) |
| `P.removeitem(k, v)` | O(log n) |
| `P.update(old_item, new_item)` | O(log n) |
| `len(P)` | O(1) |
| `is_empty(P)` | O(1) |
| `P.contains(k, v)` | O(1) |
| `P.show(i)` | O(1) |
| function `heapsorted()` | O(n log n) |
## Example for `DHeap` class
- Data to be inserted in to a priority queue must be a tuple of size $2$, where the first entry must contain priority numbers (either integer or floating-point type) and the second entry can be any object. Aside from individual insertion, a group of individual items of data can also be inserted into a priority queue. Let's do an example. Prepare data to be inserted into a priority queue in a list of tuples:
```
toInsert = [(10, 'CGK'), (9, 'BSL'), (9.2, 'IST'), (8, 'AMS'),
(7, 'BCN'), (5, 'DOH'), (3, 'BOS'), (8.7, 'AUH')]
```
- Import `DHeap` class:
```
from dheapy import DHeap
```
- Instantiate an empty priority queue object:
```
branching_factor = 3
variant = 'min'
P = DHeap(branching_factor, variant)
```
- To verify if parameters are correct, we print the object we just created
```
print(P)
```
which will result in
```
Priority Queue with 3 branching factor and min-heap
```
- Check if the priority queue is empty:
```
print(f'Is Priority Queue empty: {P.is_empty()}')
print(f'Priority Queue length = {len(P)}')
```
which will result in
```
Is Priority Queue empty: True
Priority Queue length = 0
```
- Insert the data into our empty priority queue `P`:
```
for i in toInsert:
P.insert(i[0], i[1])
```
- Check again whether the priority queue is already filled with data and its length:
```
print(f'Is Priority Queue empty: {P.is_empty()}')
print(f'Priority Queue length = {len(P)}')
```
which will print
```
Is Priority Queue empty: False
Priority Queue length = 8
```
- Use `peek()` module to display the highest priority item:
```
print(f'Highest priority: {P.peek()}')
```
we'll get
```
Highest priority: (3, 'BOS')
```
Our ternary min-heap will look like as follows:
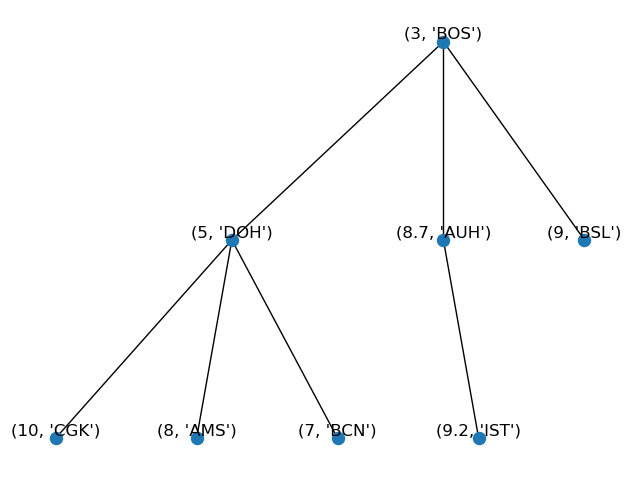
Our data will be stored in a list in an arrangement such that it starts from the root node `(3, 'BOS')`. The root's children will be stored subsequently, starting from the most left child `(5, 'DOH')` traversing horizontally through all children until the most right child `(9, 'BSL')`. Thus data in the list will be stored as `[(3, 'BOS'), (5, 'DOH'), (8.7, 'AUH'), (9, 'BSL')]`. Then children of the most left child `(5, 'DOH')` will be stored next, followed with children of `(8.7, 'AUH')`, and so on. This can be verified by using the `show(i)` module where `i` is an index number of the item position. For example, to obtain item at index $0$ or the root node, by either directly displaying like:
```
print(P.show(0))
```
with result
```
(3, 'BOS')
```
Or, to get the pair of priority number and its element individually:
```
priority, element = P.show(0)
```
then display:
```
print(priority, element)
```
Since in this example we use a ternary heap, to display all three children of the root node directly:
```
print(P.show(1))
print(P.show(2))
print(P.show(3))
```
which will give us
```
(5, 'DOH')
(8.7, 'AUH')
(9, 'BSL')
```
- Use module `delete()` to delete the current highest priority:
```
P.delete()
```
or to display the deleted item:
```
print(f'Deleted: {P.delete()}')
```
which will return
```
Deleted: (3, 'BOS')
```
- View the new highest priority:
```
print(f'Highest priority: {P.peek()}')
```
to get:
```
Highest priority: (5, 'DOH')
```
and our structure now will look like:
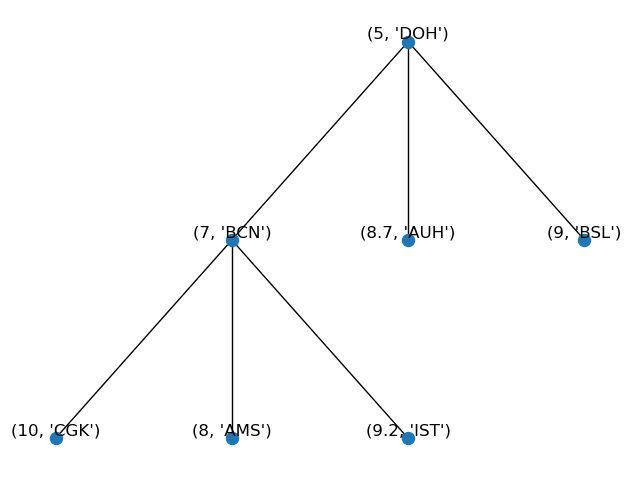
- Use `removeitem(k, v)` to remove an item from our priority queue, where `k` is a key or priority number and `v` is its element. For example, to remove `(8.7, 'AUH')`:
```
rm = P.removeitem(8.7, 'AUH')
print(f"Removed: {rm}")
```
we get
```
Removed: (8.7, 'AUH')
```
Our structure now will look like:
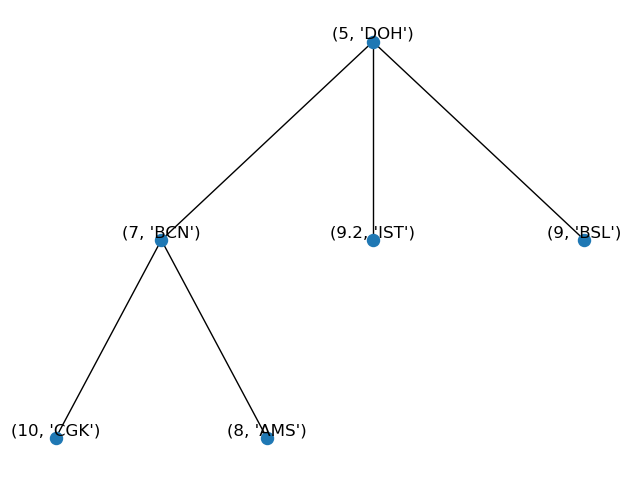
- To replace an item with a new one, use the `update()` module. For example, to replace the item `(8, AMS)` with `(3.3, 'SFO')`:
```
old_item = (8, 'AMS')
new_item = (3.3, 'SFO')
P.update(old_item, new_item)
```
and check the latest highest priority:
```
print(f'Highest priority: {P.peek()}')
```
will return
```
Highest priority: (3.3, 'SFO')
```
Our structure now will look like:
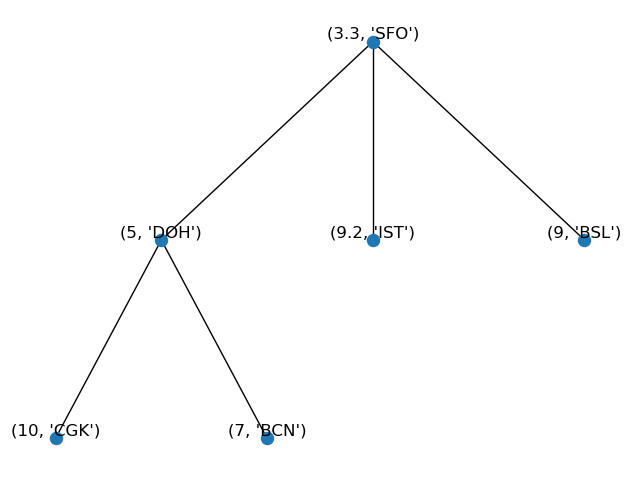
- Finally, to check if an item is in our priority queue, we can use the module `contains(k, v)` with `k` is the key or priority number of the item and `v` is its element:
```
P.contains(4.5, 'TKO')
```
will return
```
False
```
or
```
P.contains(9, 'BSL')
```
will return
```
True
```
## Example for `heapsorted` function
Import the function:
```
from dheapy import heapsorted
```
The `heapsorted()` function is used to sort a list of tuples, just like the example data for `DHeap` class above.
- To sort a list of tuples data:
```
data = [(10, 'CGK'), (9, 'BSL'), (9.2, 'IST'), (8, 'AMS'),
(7, 'BCN'), (5, 'DOH'), (3, 'BOS'), (8.7, 'AUH')]
branching_factor = 3
variant = 'min'
result = heapsorted(data, branching_factor, variant)
```
To print the `result`:
```
print(result)
```
we get
```
[(3, 'BOS'), (5, 'DOH'), (7, 'BCN'), (8, 'AMS'), (8.7, 'AUH'), (9, 'BSL'), (9.2, 'IST'), (10, 'CGK')]
```
- To sort data in a priority queue, we must transform the data into an array. Let's sort the priority queue `P` we have created in the above example. First we create an empty array, and then append the items in `P` into the array using the module `show()`:
```
array = []
for i in range(len(P)):
array.append(P.show(i))
```
Then we use the `array` for our function input argument:
```
result = heapsorted(array, branching_factor, variant)
```
printing the result, we'll get
```
[(3.3, 'SFO'), (5, 'DOH'), (7, 'BCN'), (9, 'BSL'), (9.2, 'IST'), (10, 'CGK')]
```
## References
Raw data
{
"_id": null,
"home_page": null,
"name": "dheapy",
"maintainer": null,
"docs_url": null,
"requires_python": ">=3.9",
"maintainer_email": null,
"keywords": "priority queue, heap, max-heap, min-heap, d-ary heap, binary heap, ternary heap, quaternary heap, quinary heap",
"author": null,
"author_email": "\"Vivi Andasari, PhD\" <vandasari@gmail.com>",
"download_url": "https://files.pythonhosted.org/packages/b8/85/2fe3055837c1c0704d23ef0695a5c051aecbd92e2d3dd8c2b68ae4416764/dheapy-0.1.5.tar.gz",
"platform": null,
"description": "# `dheapy`\n\n`dheapy` is a pure Python implementation of $d$-ary heap data structure for priority queue applications, which can work for both max-heap and min-heap variants. The factor $d$ in $d$-ary heap is called the branching factor and it can be equal to or greater than $2$, where $d=2$ means the heap is built with a binary tree, $d=3$ with a ternary tree, $d=4$ with a quaternary tree, and so on.\n\nThe branching factor of a tree is the maximum number of children a node can have.\n\nA $2$-ary heap or binary heap has a branching factor of $2$:\n\n\nA $3$-ary heap or ternary heap has a branching factor of $3$:\n\n\nA $4$-ary heap or quaternary heap has a branching factor of $4$:\n\n\n`dheapy` is array-based and adaptable, where arbitrary items can be removed, updated, and displayed on the go.\n\nThe library also comes with a sorting function that is based on the heap-sort algorithm to sort lists of tuples.\n\n## Installation\n\nUse the package manager [pip](https://pip.pypa.io/en/stable/) to install `dheapy`:\n\n```\npip install dheapy\n```\n\n## Prerequisites\n\nNone.\n\n## Usage\n\n1. `DHeap(branching_factor=2, variant='max')` \n Class to create an empty and perform priority queue operations (shown in the table below).\n Parameters:\n\n - `branching_factor`: `int`; default = `2`\n - `variant`: `str`, either `'max'` or `'min'`; default = `'max'`\n\n To import `DHeap` class:\n\n ```\n from dheapy import DHeap\n ```\n\n2. `heapsorted(object, branching_factor=2, variant='max')`\n Function for sorting arrays that is based on the heap sort algorithm.\n Parameters:\n\n - `object`: array or iterable\n - `branching_factor`: `int`; default = `2`\n - `variant`: `str`, either `'max'` or `'min'`; default = `'max'`\n\n To import `heapsorted()` function\n\n ```\n from dheapy import heapsorted\n ```\n\nTo create an empty priority queue with branching factor 3 and min-heap variant:\n\n```\nP = DHeap(3, 'min')\n```\n\nThe following are operations that can be performed with `DHeap` class:\n\n| **Operation** | **Description** | **Object Returned** |\n| ------------------------------ | -------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------- | ------------------- |\n| `P.insert(k,v)` | adds a new item with priority number `k` and element/description `v` into priority queue. The priority number `k` must be positive and can be of integer or floating-point type; the priority element/description `v` can be of any type. | |\n| `P.peek()` | returns the highest priority item, but without extracting/removing it from the queue. | `(k, v)` |\n| `P.delete()` | removes/deletes the highest priority item from the queue. | `(k, v)` |\n| `P.removeitem(k, v)` | removes an item with priority number `k` and element `v` from the queue. | `(k, v)` |\n| `P.update(old_item, new_item)` | updates a pair of old item (in tuple, which consists of a priority number and its element) and replaces it with a pair of new item (in tuple, which consists of a priority number and its element). This operation can also be used to update a priority number or element only. | |\n| `len(P)` | returns the number of items in priority queue `P`. | `int` |\n| `is_empty(P)` | returns `True` if priority queue `P` does not contain any items. | `True` or `False` |\n| `P.contains(k, v)` | returns `True` if priority queue `P` contains an item with priority number `k` with element `v`. | `True` or `False` |\n| `P.show(i)` | returns the item at index `i`. | `(k, v)` |\n\n## Performance\n\n| **Operation** | **Time Complexity** |\n| ------------------------------ | ------------------- |\n| `P.insert(k,v)` | O(log n) |\n| `P.peek()` | O(1) |\n| `P.delete()` | O(log n) |\n| `P.removeitem(k, v)` | O(log n) |\n| `P.update(old_item, new_item)` | O(log n) |\n| `len(P)` | O(1) |\n| `is_empty(P)` | O(1) |\n| `P.contains(k, v)` | O(1) |\n| `P.show(i)` | O(1) |\n| function `heapsorted()` | O(n log n) |\n\n## Example for `DHeap` class\n\n- Data to be inserted in to a priority queue must be a tuple of size $2$, where the first entry must contain priority numbers (either integer or floating-point type) and the second entry can be any object. Aside from individual insertion, a group of individual items of data can also be inserted into a priority queue. Let's do an example. Prepare data to be inserted into a priority queue in a list of tuples:\n\n```\ntoInsert = [(10, 'CGK'), (9, 'BSL'), (9.2, 'IST'), (8, 'AMS'),\n (7, 'BCN'), (5, 'DOH'), (3, 'BOS'), (8.7, 'AUH')]\n```\n\n- Import `DHeap` class:\n\n```\nfrom dheapy import DHeap\n```\n\n- Instantiate an empty priority queue object:\n\n```\nbranching_factor = 3\nvariant = 'min'\n\nP = DHeap(branching_factor, variant)\n```\n\n- To verify if parameters are correct, we print the object we just created\n\n```\nprint(P)\n```\n\nwhich will result in\n\n```\nPriority Queue with 3 branching factor and min-heap\n```\n\n- Check if the priority queue is empty:\n\n```\nprint(f'Is Priority Queue empty: {P.is_empty()}')\nprint(f'Priority Queue length = {len(P)}')\n```\n\nwhich will result in\n\n```\nIs Priority Queue empty: True\nPriority Queue length = 0\n```\n\n- Insert the data into our empty priority queue `P`:\n\n```\nfor i in toInsert:\n P.insert(i[0], i[1])\n```\n\n- Check again whether the priority queue is already filled with data and its length:\n\n```\nprint(f'Is Priority Queue empty: {P.is_empty()}')\nprint(f'Priority Queue length = {len(P)}')\n```\n\nwhich will print\n\n```\nIs Priority Queue empty: False\nPriority Queue length = 8\n```\n\n- Use `peek()` module to display the highest priority item:\n\n```\nprint(f'Highest priority: {P.peek()}')\n```\n\nwe'll get\n\n```\nHighest priority: (3, 'BOS')\n```\n\nOur ternary min-heap will look like as follows:\n\n\n\nOur data will be stored in a list in an arrangement such that it starts from the root node `(3, 'BOS')`. The root's children will be stored subsequently, starting from the most left child `(5, 'DOH')` traversing horizontally through all children until the most right child `(9, 'BSL')`. Thus data in the list will be stored as `[(3, 'BOS'), (5, 'DOH'), (8.7, 'AUH'), (9, 'BSL')]`. Then children of the most left child `(5, 'DOH')` will be stored next, followed with children of `(8.7, 'AUH')`, and so on. This can be verified by using the `show(i)` module where `i` is an index number of the item position. For example, to obtain item at index $0$ or the root node, by either directly displaying like:\n\n```\nprint(P.show(0))\n```\n\nwith result\n\n```\n(3, 'BOS')\n```\n\nOr, to get the pair of priority number and its element individually:\n\n```\npriority, element = P.show(0)\n```\n\nthen display:\n\n```\nprint(priority, element)\n```\n\nSince in this example we use a ternary heap, to display all three children of the root node directly:\n\n```\nprint(P.show(1))\nprint(P.show(2))\nprint(P.show(3))\n```\n\nwhich will give us\n\n```\n(5, 'DOH')\n(8.7, 'AUH')\n(9, 'BSL')\n```\n\n- Use module `delete()` to delete the current highest priority:\n\n```\nP.delete()\n```\n\nor to display the deleted item:\n\n```\nprint(f'Deleted: {P.delete()}')\n```\n\nwhich will return\n\n```\nDeleted: (3, 'BOS')\n```\n\n- View the new highest priority:\n\n```\nprint(f'Highest priority: {P.peek()}')\n```\n\nto get:\n\n```\nHighest priority: (5, 'DOH')\n```\n\nand our structure now will look like:\n\n\n- Use `removeitem(k, v)` to remove an item from our priority queue, where `k` is a key or priority number and `v` is its element. For example, to remove `(8.7, 'AUH')`:\n\n```\nrm = P.removeitem(8.7, 'AUH')\nprint(f\"Removed: {rm}\")\n```\n\nwe get\n\n```\nRemoved: (8.7, 'AUH')\n```\n\nOur structure now will look like:\n\n\n- To replace an item with a new one, use the `update()` module. For example, to replace the item `(8, AMS)` with `(3.3, 'SFO')`:\n\n```\nold_item = (8, 'AMS')\nnew_item = (3.3, 'SFO')\nP.update(old_item, new_item)\n```\n\nand check the latest highest priority:\n\n```\nprint(f'Highest priority: {P.peek()}')\n```\n\nwill return\n\n```\nHighest priority: (3.3, 'SFO')\n```\n\nOur structure now will look like:\n\n\n- Finally, to check if an item is in our priority queue, we can use the module `contains(k, v)` with `k` is the key or priority number of the item and `v` is its element:\n\n```\nP.contains(4.5, 'TKO')\n```\n\nwill return\n\n```\nFalse\n```\n\nor\n\n```\nP.contains(9, 'BSL')\n```\n\nwill return\n\n```\nTrue\n```\n\n## Example for `heapsorted` function\n\nImport the function:\n\n```\nfrom dheapy import heapsorted\n```\n\nThe `heapsorted()` function is used to sort a list of tuples, just like the example data for `DHeap` class above.\n\n- To sort a list of tuples data:\n\n```\ndata = [(10, 'CGK'), (9, 'BSL'), (9.2, 'IST'), (8, 'AMS'),\n (7, 'BCN'), (5, 'DOH'), (3, 'BOS'), (8.7, 'AUH')]\n\nbranching_factor = 3\nvariant = 'min'\nresult = heapsorted(data, branching_factor, variant)\n```\n\nTo print the `result`:\n\n```\nprint(result)\n```\n\nwe get\n\n```\n[(3, 'BOS'), (5, 'DOH'), (7, 'BCN'), (8, 'AMS'), (8.7, 'AUH'), (9, 'BSL'), (9.2, 'IST'), (10, 'CGK')]\n```\n\n- To sort data in a priority queue, we must transform the data into an array. Let's sort the priority queue `P` we have created in the above example. First we create an empty array, and then append the items in `P` into the array using the module `show()`:\n\n```\narray = []\n\nfor i in range(len(P)):\n array.append(P.show(i))\n```\n\nThen we use the `array` for our function input argument:\n\n```\nresult = heapsorted(array, branching_factor, variant)\n```\n\nprinting the result, we'll get\n\n```\n[(3.3, 'SFO'), (5, 'DOH'), (7, 'BCN'), (9, 'BSL'), (9.2, 'IST'), (10, 'CGK')]\n```\n\n## References\n",
"bugtrack_url": null,
"license": null,
"summary": "Max/min d-ary heap implementation for priority queues.",
"version": "0.1.5",
"project_urls": {
"Homepage": "https://github.com/vandasari/dheapy",
"Issues": "https://github.com/vandasari/dheapy/issues",
"Repository": "https://github.com/vandasari/dheapy"
},
"split_keywords": [
"priority queue",
" heap",
" max-heap",
" min-heap",
" d-ary heap",
" binary heap",
" ternary heap",
" quaternary heap",
" quinary heap"
],
"urls": [
{
"comment_text": "",
"digests": {
"blake2b_256": "474f6e7e0cd4364d35390a0744e1cb714fa6bd64f64ed464cea9afeec0e6c6b5",
"md5": "4ce581467c07f5e75a4a83a5b158f38a",
"sha256": "89954e74864cf8456dcbcf0f3704ef7a6093f24dda67ce36007ed2f60bd21a74"
},
"downloads": -1,
"filename": "dheapy-0.1.5-py3-none-any.whl",
"has_sig": false,
"md5_digest": "4ce581467c07f5e75a4a83a5b158f38a",
"packagetype": "bdist_wheel",
"python_version": "py3",
"requires_python": ">=3.9",
"size": 8005,
"upload_time": "2024-12-21T03:04:18",
"upload_time_iso_8601": "2024-12-21T03:04:18.813671Z",
"url": "https://files.pythonhosted.org/packages/47/4f/6e7e0cd4364d35390a0744e1cb714fa6bd64f64ed464cea9afeec0e6c6b5/dheapy-0.1.5-py3-none-any.whl",
"yanked": false,
"yanked_reason": null
},
{
"comment_text": "",
"digests": {
"blake2b_256": "b8852fe3055837c1c0704d23ef0695a5c051aecbd92e2d3dd8c2b68ae4416764",
"md5": "0075edc8a4a058256f6e520823112451",
"sha256": "8142fea1e4917b02e1446aa1aa02e5c24fe76594bc06e42bb39907593ebbc0df"
},
"downloads": -1,
"filename": "dheapy-0.1.5.tar.gz",
"has_sig": false,
"md5_digest": "0075edc8a4a058256f6e520823112451",
"packagetype": "sdist",
"python_version": "source",
"requires_python": ">=3.9",
"size": 10802,
"upload_time": "2024-12-21T03:04:25",
"upload_time_iso_8601": "2024-12-21T03:04:25.296652Z",
"url": "https://files.pythonhosted.org/packages/b8/85/2fe3055837c1c0704d23ef0695a5c051aecbd92e2d3dd8c2b68ae4416764/dheapy-0.1.5.tar.gz",
"yanked": false,
"yanked_reason": null
}
],
"upload_time": "2024-12-21 03:04:25",
"github": true,
"gitlab": false,
"bitbucket": false,
"codeberg": false,
"github_user": "vandasari",
"github_project": "dheapy",
"travis_ci": false,
"coveralls": false,
"github_actions": false,
"lcname": "dheapy"
}
