# Adaptive, Elastic Multi-Server Downloading
[][pypi status]
[][pypi status]
[][read the docs]
[][tests]
[][codecov]
[][repo]
[][downloads]
[][dlrate]
[][codacy]
[][snyk]
[pypi status]: https://pypi.org/project/flardl/
[read the docs]: https://flardl.readthedocs.io/
[tests]: https://github.com/hydrationdynamics/flardl/actions?workflow=Tests
[codecov]: https://app.codecov.io/gh/hydrationdynamics/flardl
[repo]: https://github.com/hydrationdynamics/flardl
[downloads]: https://pepy.tech/project/flardl
[dlrate]: https://github.com/hydrationdynamics/flardl
[codacy]: https://www.codacy.com/gh/hydrationdynamics/flardl?utm_source=github.com&utm_medium=referral&utm_content=hydrationdynamics/zeigen&utm_campaign=Badge_Grade
[snyk]: https://snyk.io/advisor/python/flardl
> Who would flardls bear?
[][logo license]
[logo license]: https://raw.githubusercontent.com/hydrationdynamics/flardl/main/LICENSE.logo.txt
## Towards Sustainable Downloading
Small amounts of Time spent waiting on downloads adds
up over thousands over uses, both in human terms and
in terms of energy usage. If we are to respond to the
challenge of climate change, it's important to consider
the efficiency and sustainability of computations we
launch. Downloads may consume only a tiny fraction
of cycles for computational science, but they often
consume a noticeable fraction of wall-clock time.
While the download bit rate of one's local WAN link is the limit
that matters most, downloading times are also governed by time
spent waiting on handshaking to start transfers or to acknowledge
data received. **Synchronous downloads are highly energy-inefficient**
because hardware still consumes energy during waits. A more sustainable
approach is to arrange the computational graph to do transfers
simultaneously and asynchronously using multiple simultaneous downloads.
The situation is made more complicated when downloads can be
launched from anywhere in the world to a federated set of servers,
possibly involving content delivery networks. Optimal download
performance in that situation depends on adapting to network
conditions and server loads, typically without no information
other than the last download times of files.
_Flardl_ downloads lists of files using an approach that
adapts to local conditions and is elastic with respect
to changes in network performance and server loads.
_Flardl_ achieves download rates **typically more than
300X higher** than synchronous utilities such as _curl_,
while allowing use of multiple servers to provide superior
protection against blacklisting. Download rates depend
on network bandwidth, latencies, list length, file sizes,
and HTTP protocol used, but using _flardl_, even a single
server on another continent can usually saturate a gigabit
cable connection after about 50 files.
## Queueing on Long Tails
Typically, one doesn't know much about the list of files to
be downloaded, nor about the state of the servers one is going
to use to download them. Once the first file request has been
made to a given server, download software has only one means of
control, whether to launch another download or wait. Making
that decision well depends on making good guesses about likely
return times.
Collections of files generated by natural or human activity such
as natural-language writing, protein structure determination,
or genome sequencing tend to have **size distributions with
long tails**. Such distributions have more big files than
small files at a given size above or below the most-common (_modal_)
size. Analytical forms of long-tail distributions include Zipf,
power-law, and log-norm distributions. A real-world example of a
long-tail distribution is shown below, which plots the file-size
histogram for 1000 randomly-sampled CIF structure files from the
[Protein Data Bank](https://rcsb.org), along with a kernel-density
estimate and fits to log-normal and normal distributions.
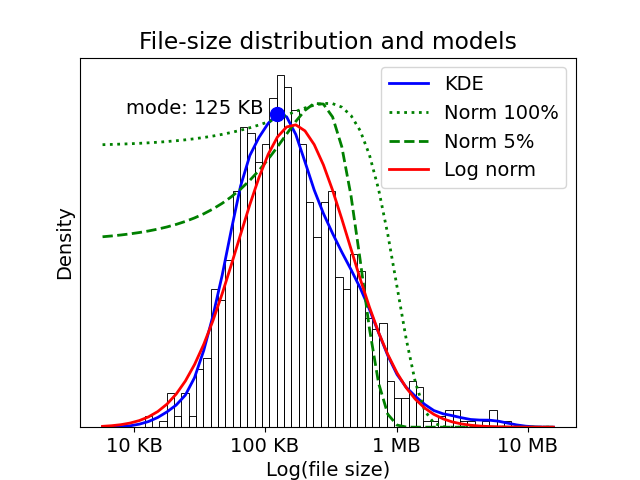
Queueing algorithms that rely upon per-file rates as the
pricipal control mechanism implicitly assume that queue
statistics can be approximated with a normal-ish distribution,
meaning one without a long tail. In making that assumption,
they largely ignore the effects of big files on overall
download statistics. Such algorithms inevitably encounter
problems because **mean values are neither stable nor
characteristic of the distribution**. For example, as can be
seen in the fits above, the mean and standard distribution
of samples drawn from a long-tail distribution tend to grow
with increasing sample size. The fit of a normal distribution
to a sample of 5% of the data (dashed line) gives a markedly
lower mean and standard deviation than the fit to all points
(dotted line), and both fits are poor. The mean tends to grow
with sample size because larger samples are more likely to
include a huge file that dominates the average value.
Algorithms that employ average per-file rates or times as the
primary means of control will launch requests too slowly most
of the time while letting queues run too deep when big downloads
are encountered. While the _mean_ per-file download time isn't a
good statistic, **control based on _modal_ per-file file statistics
can be more consistent**. For example, the modal per-file download
time $\tilde{\tau}$, where the tilde indicates a modal value), is
fairly consistent across sample size, and transfer algorithms based
on that statistic will perform consistently, at least on timescales
over which network and server performance are stable.
### Queue Depth is Toxic
At first glance, running at high queue depths seems attractive.
One of the simplest queueing algorithms would to simply put every
job in a queue at startup and let the server(s) handle requests
in parallel up to their individual critical queue depths, above
which depths they are responsible for serialization . But such
non-adaptive non-elastic algorithms
give poor real-world performance or multiple reasons. First, if
there is more than one server queue, differing file sizes and
transfer rates will result in the queueing equivalent of
[Amdahl's law](https://en.wikipedia.org/wiki/Amdahl%27s_law),
by **creating an overhang** where one server still has multiple
files queued up to serve while others have completed all requests.
The server with the overhang is also not guaranteed to be the
fastest one.
If a server decides you are abusing its queue policies,
it may take action that hurts your current and future downloads.
Most public-facing servers have policies to recognize and defend
against Denial-Of-Service (DOS) attacks and a large number of
requests from a single IP address in a short
time is the main hallmark of a DOS attack. The minimal response
to a DOS event causes the server to dump your latest requests,
a minor nuisance. Worse is if the server responds by severely
throttling further requests from your IP address for hours
or sometime days. But in the worst case, your IP address can get the
"death penalty" of being put on a permanent blacklist for throttling
or blockage that may require manual intervention by someone in control
of the server to get removed from. Blacklisting might not even be your
personal fault, but a collective problem. I have seen a practical class
of 20 students brought to a complete halt by a 24-hour blacklisting
of the institution's public IP address by a government site. Until methods
are developed for servers to publish their "play-friendly" values and to
whitelist known-friendly clients, the highest priority for downloading
algorithms must be to **avoid blacklisting by a server by minimizing
queue depth**. At the other extreme, the absolute minimum queue depth is
retreating back to synchronous downloading. How can we balance
the competing demands of speed while avoiding blacklisting?
### A Fishing Metaphor
An analogy might help us here. Let's say you are a person who
enjoys keeping track of statistics, and you decide to try
fishing. At first, you have a single fishing rod and you go
fishing at a series of local lakes where your catch consists
of **small fishes called "crappies"**. Your records reval
that while the rate of catching fishes can vary from day to
day--fish might be hungry or not--the average size of a crappie
from a given pond is pretty stable. Bigger ponds tend to have
bigger crappies in them, and it might take slightly longer to
reel in a bigger crappie than a small one, but the rate of
catching crappies averages out pretty quickly.
You love fishing so much that one day you drive
to the coast and charter a fishing boat. On that boat,
you can set out as many lines as you want (up to some limit)
and fish in parallel. At first, you catch mostly small fishes
that are the ocean-going equivalent of crappies. But
eventually you hook a small whale. Not does it take a lot of
your time and attention to reel in the whale, but landing
it totally skews the average weight and catch rate. You and
your crew can only effecively reel in so many hooked lines at
once. Putting out more lines than that effective limit of hooked
plus waiting-to-be-hooked lines only results in more wait times
in the ocean.
Our theory of fishing says to **put out lines at the usual rate
of catching crappies but limit the number of lines to deal with
whales**. The most probable rate of catching modal-sized fies
will be optimistic, but you can delay putting out more lines if
you reach the maximum number of lines your boat can handle. Once
you catch enough to be able to estimate how fish are biting, you
can back off the number of lines to the number that you and your
crew can handle at a time that day.
### Adaptilastic Queueing
_Flardl_ implements a method I call "adaptilastic"
queueing to deliver robust performance in real situations.
Adaptilastic queueing uses timing on transfers from an initial
period—launched using optimistic assumptions—to
optimize later transfers by using the minimum total depth over
all quese that will plateau the download bit rate while avoiding
excess queue depth on any given server. _Flardl_ distinguishes
among four different operating regimes:
- **Naive**, where no transfers have ever been completed,
- **Informed**, where information from a previous run
is available,
- **Arriving**, where information from at least one transfer
to at least one server has occurred,
- **Updated**, where a sufficient number of transfers has
occurred that file transfers may be characterized, for an
least one server.
The optimistic rate at which _flardl_ launches requests for
a given server $j$ is given by the expectation rates for
modal-sized files with small queue depths as
$`
\begin{equation}
k_j =
\left\{ \begin{array}{ll}
\tilde{S} B_{\rm max} / D_j & \mbox{if naive}, \\
\tilde{\tau}_{\rm prev} B_{\rm max} / B_{\rm prev}
& \mbox{if informed}, \\
1/(t_{\rm cur} - I_{\rm first})
& \mbox{if arriving,} \\
\tilde{\tau_j} & \mbox{if updated,} \\
\end{array} \right.
\end{equation}
`$
where
- $\tilde{S}$ is the modal file size for the collection
(an input parameter),
- $B_{\rm max}$ is the maximum permitted download rate
(an input parameter),
- $D_j$ is the server queue depth at launch,
- $\tilde{\tau}_{\rm prev}$ is the modal file arrival rate
for the previous session,
- $B_{\rm prev}$ is the plateau download bit rate for
the previous session,
- $t_{\rm cur}$ is the current time,
- $I_{\rm first}$ is the initiation time for the first
transfer to arrive,
- and $\tilde{\tau_j}$ is the modal file transfer rate
for the current session with the server.
After waiting an exponentially-distributed stochastic period
given by the applicable value for $k_j$, testing is done
against four limits calculated by the methods in the [theory]
section:
- The per-server queue depth must be less than the maximum
$D_{{\rm max}_j}$, an input parameter (default 100), revised
downward and stored for future use if any queue requests are
rejected (default 100),
- In the updated state with per-server stats available, the
per-server queue depth must be less than the calculated critical
per-server queue depth $D_{{\rm crit}_j}$,
- In the updated state, the total queue depth must be less than
the saturation queue depth, $D_{\rm sat}$, at which the
current download bit rate $B_{\rm cur}$ saturates,
- The curremt download bit rate must be less than $B_{\rm max}$,
the maximum bandwidth allowed.
If any of the limits are exceeded, a stochastic wait period
at the inverse of the current per-server rate $k_j$ is added
until the limit is no longer exceeded.
### If File Sizes are Known
The adapilastic algorithm assumes that file sizes are randomly-ordered
in the list. But what if we know the file sizes beforehand? The server
that draws the biggest file is most likely to finish last, so it's
important for that file to be started on the lowest-latency server as
soon as one has current information about which server is indeed
fastest (i.e., by reaching the _arriving_ state). The way that _flardl_
optimizes downloads when provided a dictionary of relative file sizes
is to sort the incoming list of downloads into two lists. The first
list (the crappies list) is sorted into tiers of files with the size
of the tier equal to the number of servers $N_{\rm serv}$ in use. The
0th tier is the smallest $N_{\rm serv}$ files, the next tier is the
largest $N_{\rm serv}$ files below a cutoff file size (default of 2x the
modal file size), and alternating between the smallest and biggest
crappies out to $N_{\min}$ files. The second list is all other files,
sorted in order of descending file size (that is, starting with the
whales). _Flardl_ waits until it enters the _updated_ state, with all
files from the first list returned before drawing from the second list
so that the fastest server will definitively get the job of sending the
biggest file, thus minimizing waits for overhanging files.
## Requirements
_Flardl_ is tested under the highest supported python version on
Linux, MacOS, and Windows and under the lowest supported python version
on Linux. Under the hood, _flardl_ relies on
[httpx](https://www.python-httpx.org/) and is supported
on whatever platforms that library works for both HTTP/1.1
and HTTP/2.
## Installation
You can install _Flardl_ via [pip] from [PyPI]:
```console
$ pip install flardl
```
## Usage
_Flardl_ has no CLI and does no I/O other than downloading and writing
files. See test examples for usage.
## Contributing
Contributions are very welcome. To learn more, see the [Contributor Guide].
## License
Distributed under the terms of the [BSD 3-clause license][license],
_flardl_ is free and open source software.
## Issues
If you encounter any problems, please [file an issue] along with a
detailed description.
## Credits
_Flardl_ was written by Joel Berendzen.
[pypi]: https://pypi.org/
[file an issue]: https://github.com/hydrationdynamics/flardl/issues
[pip]: https://pip.pypa.io/
[theory]: https://github.com/hydrationdynamics/flardl/blob/main/THEORY.md
<!-- github-only -->
[license]: https://github.com/hydrationdynamics/flardl/blob/main/LICENSE
[contributor guide]: https://github.com/hydrationdynamics/flardl/blob/main/CONTRIBUTING.md
Raw data
{
"_id": null,
"home_page": "",
"name": "flardl",
"maintainer": "",
"docs_url": null,
"requires_python": "<3.13,>=3.9",
"maintainer_email": "",
"keywords": "downloading asynchronous multidispatching queueing adaptive elastic adaptilastic federated high-performance",
"author": "",
"author_email": "Joel Berendzen <joel@generisbio.com>",
"download_url": "https://files.pythonhosted.org/packages/19/90/d9d0c5aabbde623c84e58b5aad77af6ded2b3ea42ed126281830db2522d6/flardl-0.0.8.2.tar.gz",
"platform": null,
"description": "# Adaptive, Elastic Multi-Server Downloading\n\n[][pypi status]\n[][pypi status]\n[][read the docs]\n[][tests]\n[][codecov]\n[][repo]\n[][downloads]\n[][dlrate]\n[][codacy]\n[][snyk]\n\n[pypi status]: https://pypi.org/project/flardl/\n[read the docs]: https://flardl.readthedocs.io/\n[tests]: https://github.com/hydrationdynamics/flardl/actions?workflow=Tests\n[codecov]: https://app.codecov.io/gh/hydrationdynamics/flardl\n[repo]: https://github.com/hydrationdynamics/flardl\n[downloads]: https://pepy.tech/project/flardl\n[dlrate]: https://github.com/hydrationdynamics/flardl\n[codacy]: https://www.codacy.com/gh/hydrationdynamics/flardl?utm_source=github.com&utm_medium=referral&utm_content=hydrationdynamics/zeigen&utm_campaign=Badge_Grade\n[snyk]: https://snyk.io/advisor/python/flardl\n\n> Who would flardls bear?\n\n[][logo license]\n\n[logo license]: https://raw.githubusercontent.com/hydrationdynamics/flardl/main/LICENSE.logo.txt\n\n## Towards Sustainable Downloading\n\nSmall amounts of Time spent waiting on downloads adds\nup over thousands over uses, both in human terms and\nin terms of energy usage. If we are to respond to the\nchallenge of climate change, it's important to consider\nthe efficiency and sustainability of computations we\nlaunch. Downloads may consume only a tiny fraction\nof cycles for computational science, but they often\nconsume a noticeable fraction of wall-clock time.\n\nWhile the download bit rate of one's local WAN link is the limit\nthat matters most, downloading times are also governed by time\nspent waiting on handshaking to start transfers or to acknowledge\ndata received. **Synchronous downloads are highly energy-inefficient**\nbecause hardware still consumes energy during waits. A more sustainable\napproach is to arrange the computational graph to do transfers\nsimultaneously and asynchronously using multiple simultaneous downloads.\nThe situation is made more complicated when downloads can be\nlaunched from anywhere in the world to a federated set of servers,\npossibly involving content delivery networks. Optimal download\nperformance in that situation depends on adapting to network\nconditions and server loads, typically without no information\nother than the last download times of files.\n\n_Flardl_ downloads lists of files using an approach that\nadapts to local conditions and is elastic with respect\nto changes in network performance and server loads.\n_Flardl_ achieves download rates **typically more than\n300X higher** than synchronous utilities such as _curl_,\nwhile allowing use of multiple servers to provide superior\nprotection against blacklisting. Download rates depend\non network bandwidth, latencies, list length, file sizes,\nand HTTP protocol used, but using _flardl_, even a single\nserver on another continent can usually saturate a gigabit\ncable connection after about 50 files.\n\n## Queueing on Long Tails\n\nTypically, one doesn't know much about the list of files to\nbe downloaded, nor about the state of the servers one is going\nto use to download them. Once the first file request has been\nmade to a given server, download software has only one means of\ncontrol, whether to launch another download or wait. Making\nthat decision well depends on making good guesses about likely\nreturn times.\n\nCollections of files generated by natural or human activity such\nas natural-language writing, protein structure determination,\nor genome sequencing tend to have **size distributions with\nlong tails**. Such distributions have more big files than\nsmall files at a given size above or below the most-common (_modal_)\nsize. Analytical forms of long-tail distributions include Zipf,\npower-law, and log-norm distributions. A real-world example of a\nlong-tail distribution is shown below, which plots the file-size\nhistogram for 1000 randomly-sampled CIF structure files from the\n[Protein Data Bank](https://rcsb.org), along with a kernel-density\nestimate and fits to log-normal and normal distributions.\n\n\n\nQueueing algorithms that rely upon per-file rates as the\npricipal control mechanism implicitly assume that queue\nstatistics can be approximated with a normal-ish distribution,\nmeaning one without a long tail. In making that assumption,\nthey largely ignore the effects of big files on overall\ndownload statistics. Such algorithms inevitably encounter\nproblems because **mean values are neither stable nor\ncharacteristic of the distribution**. For example, as can be\nseen in the fits above, the mean and standard distribution\nof samples drawn from a long-tail distribution tend to grow\nwith increasing sample size. The fit of a normal distribution\nto a sample of 5% of the data (dashed line) gives a markedly\nlower mean and standard deviation than the fit to all points\n(dotted line), and both fits are poor. The mean tends to grow\nwith sample size because larger samples are more likely to\ninclude a huge file that dominates the average value.\n\nAlgorithms that employ average per-file rates or times as the\nprimary means of control will launch requests too slowly most\nof the time while letting queues run too deep when big downloads\nare encountered. While the _mean_ per-file download time isn't a\ngood statistic, **control based on _modal_ per-file file statistics\ncan be more consistent**. For example, the modal per-file download\ntime $\\tilde{\\tau}$, where the tilde indicates a modal value), is\nfairly consistent across sample size, and transfer algorithms based\non that statistic will perform consistently, at least on timescales\nover which network and server performance are stable.\n\n### Queue Depth is Toxic\n\nAt first glance, running at high queue depths seems attractive.\nOne of the simplest queueing algorithms would to simply put every\njob in a queue at startup and let the server(s) handle requests\nin parallel up to their individual critical queue depths, above\nwhich depths they are responsible for serialization . But such\nnon-adaptive non-elastic algorithms\ngive poor real-world performance or multiple reasons. First, if\nthere is more than one server queue, differing file sizes and\ntransfer rates will result in the queueing equivalent of\n[Amdahl's law](https://en.wikipedia.org/wiki/Amdahl%27s_law),\nby **creating an overhang** where one server still has multiple\nfiles queued up to serve while others have completed all requests.\nThe server with the overhang is also not guaranteed to be the\nfastest one.\n\nIf a server decides you are abusing its queue policies,\nit may take action that hurts your current and future downloads.\nMost public-facing servers have policies to recognize and defend\nagainst Denial-Of-Service (DOS) attacks and a large number of\nrequests from a single IP address in a short\ntime is the main hallmark of a DOS attack. The minimal response\nto a DOS event causes the server to dump your latest requests,\na minor nuisance. Worse is if the server responds by severely\nthrottling further requests from your IP address for hours\nor sometime days. But in the worst case, your IP address can get the\n\"death penalty\" of being put on a permanent blacklist for throttling\nor blockage that may require manual intervention by someone in control\nof the server to get removed from. Blacklisting might not even be your\npersonal fault, but a collective problem. I have seen a practical class\nof 20 students brought to a complete halt by a 24-hour blacklisting\nof the institution's public IP address by a government site. Until methods\nare developed for servers to publish their \"play-friendly\" values and to\nwhitelist known-friendly clients, the highest priority for downloading\nalgorithms must be to **avoid blacklisting by a server by minimizing\nqueue depth**. At the other extreme, the absolute minimum queue depth is\nretreating back to synchronous downloading. How can we balance\nthe competing demands of speed while avoiding blacklisting?\n\n### A Fishing Metaphor\n\nAn analogy might help us here. Let's say you are a person who\nenjoys keeping track of statistics, and you decide to try\nfishing. At first, you have a single fishing rod and you go\nfishing at a series of local lakes where your catch consists\nof **small fishes called \"crappies\"**. Your records reval\nthat while the rate of catching fishes can vary from day to\nday--fish might be hungry or not--the average size of a crappie\nfrom a given pond is pretty stable. Bigger ponds tend to have\nbigger crappies in them, and it might take slightly longer to\nreel in a bigger crappie than a small one, but the rate of\ncatching crappies averages out pretty quickly.\n\nYou love fishing so much that one day you drive\nto the coast and charter a fishing boat. On that boat,\nyou can set out as many lines as you want (up to some limit)\nand fish in parallel. At first, you catch mostly small fishes\nthat are the ocean-going equivalent of crappies. But\neventually you hook a small whale. Not does it take a lot of\nyour time and attention to reel in the whale, but landing\nit totally skews the average weight and catch rate. You and\nyour crew can only effecively reel in so many hooked lines at\nonce. Putting out more lines than that effective limit of hooked\nplus waiting-to-be-hooked lines only results in more wait times\nin the ocean.\n\nOur theory of fishing says to **put out lines at the usual rate\nof catching crappies but limit the number of lines to deal with\nwhales**. The most probable rate of catching modal-sized fies\nwill be optimistic, but you can delay putting out more lines if\nyou reach the maximum number of lines your boat can handle. Once\nyou catch enough to be able to estimate how fish are biting, you\ncan back off the number of lines to the number that you and your\ncrew can handle at a time that day.\n\n### Adaptilastic Queueing\n\n_Flardl_ implements a method I call \"adaptilastic\"\nqueueing to deliver robust performance in real situations.\nAdaptilastic queueing uses timing on transfers from an initial\nperiod—launched using optimistic assumptions—to\noptimize later transfers by using the minimum total depth over\nall quese that will plateau the download bit rate while avoiding\nexcess queue depth on any given server. _Flardl_ distinguishes\namong four different operating regimes:\n\n- **Naive**, where no transfers have ever been completed,\n- **Informed**, where information from a previous run\n is available,\n- **Arriving**, where information from at least one transfer\n to at least one server has occurred,\n- **Updated**, where a sufficient number of transfers has\n occurred that file transfers may be characterized, for an\n least one server.\n\nThe optimistic rate at which _flardl_ launches requests for\na given server $j$ is given by the expectation rates for\nmodal-sized files with small queue depths as\n\n$`\n \\begin{equation}\n k_j =\n \\left\\{ \\begin{array}{ll}\n \\tilde{S} B_{\\rm max} / D_j & \\mbox{if naive}, \\\\\n \\tilde{\\tau}_{\\rm prev} B_{\\rm max} / B_{\\rm prev}\n & \\mbox{if informed}, \\\\\n 1/(t_{\\rm cur} - I_{\\rm first})\n & \\mbox{if arriving,} \\\\\n \\tilde{\\tau_j} & \\mbox{if updated,} \\\\\n \\end{array} \\right.\n \\end{equation}\n`$\n\nwhere\n\n- $\\tilde{S}$ is the modal file size for the collection\n (an input parameter),\n- $B_{\\rm max}$ is the maximum permitted download rate\n (an input parameter),\n- $D_j$ is the server queue depth at launch,\n- $\\tilde{\\tau}_{\\rm prev}$ is the modal file arrival rate\n for the previous session,\n- $B_{\\rm prev}$ is the plateau download bit rate for\n the previous session,\n- $t_{\\rm cur}$ is the current time,\n- $I_{\\rm first}$ is the initiation time for the first\n transfer to arrive,\n- and $\\tilde{\\tau_j}$ is the modal file transfer rate\n for the current session with the server.\n\nAfter waiting an exponentially-distributed stochastic period\ngiven by the applicable value for $k_j$, testing is done\nagainst four limits calculated by the methods in the [theory]\nsection:\n\n- The per-server queue depth must be less than the maximum\n $D_{{\\rm max}_j}$, an input parameter (default 100), revised\n downward and stored for future use if any queue requests are\n rejected (default 100),\n- In the updated state with per-server stats available, the\n per-server queue depth must be less than the calculated critical\n per-server queue depth $D_{{\\rm crit}_j}$,\n- In the updated state, the total queue depth must be less than\n the saturation queue depth, $D_{\\rm sat}$, at which the\n current download bit rate $B_{\\rm cur}$ saturates,\n- The curremt download bit rate must be less than $B_{\\rm max}$,\n the maximum bandwidth allowed.\n\nIf any of the limits are exceeded, a stochastic wait period\nat the inverse of the current per-server rate $k_j$ is added\nuntil the limit is no longer exceeded.\n\n### If File Sizes are Known\n\nThe adapilastic algorithm assumes that file sizes are randomly-ordered\nin the list. But what if we know the file sizes beforehand? The server\nthat draws the biggest file is most likely to finish last, so it's\nimportant for that file to be started on the lowest-latency server as\nsoon as one has current information about which server is indeed\nfastest (i.e., by reaching the _arriving_ state). The way that _flardl_\noptimizes downloads when provided a dictionary of relative file sizes\nis to sort the incoming list of downloads into two lists. The first\nlist (the crappies list) is sorted into tiers of files with the size\nof the tier equal to the number of servers $N_{\\rm serv}$ in use. The\n0th tier is the smallest $N_{\\rm serv}$ files, the next tier is the\nlargest $N_{\\rm serv}$ files below a cutoff file size (default of 2x the\nmodal file size), and alternating between the smallest and biggest\ncrappies out to $N_{\\min}$ files. The second list is all other files,\nsorted in order of descending file size (that is, starting with the\nwhales). _Flardl_ waits until it enters the _updated_ state, with all\nfiles from the first list returned before drawing from the second list\nso that the fastest server will definitively get the job of sending the\nbiggest file, thus minimizing waits for overhanging files.\n\n## Requirements\n\n_Flardl_ is tested under the highest supported python version on\nLinux, MacOS, and Windows and under the lowest supported python version\non Linux. Under the hood, _flardl_ relies on\n[httpx](https://www.python-httpx.org/) and is supported\non whatever platforms that library works for both HTTP/1.1\nand HTTP/2.\n\n## Installation\n\nYou can install _Flardl_ via [pip] from [PyPI]:\n\n```console\n$ pip install flardl\n```\n\n## Usage\n\n_Flardl_ has no CLI and does no I/O other than downloading and writing\nfiles. See test examples for usage.\n\n## Contributing\n\nContributions are very welcome. To learn more, see the [Contributor Guide].\n\n## License\n\nDistributed under the terms of the [BSD 3-clause license][license],\n_flardl_ is free and open source software.\n\n## Issues\n\nIf you encounter any problems, please [file an issue] along with a\ndetailed description.\n\n## Credits\n\n_Flardl_ was written by Joel Berendzen.\n\n[pypi]: https://pypi.org/\n[file an issue]: https://github.com/hydrationdynamics/flardl/issues\n[pip]: https://pip.pypa.io/\n[theory]: https://github.com/hydrationdynamics/flardl/blob/main/THEORY.md\n\n<!-- github-only -->\n\n[license]: https://github.com/hydrationdynamics/flardl/blob/main/LICENSE\n[contributor guide]: https://github.com/hydrationdynamics/flardl/blob/main/CONTRIBUTING.md\n",
"bugtrack_url": null,
"license": "BSD-3-Clause",
"summary": "Adaptive Elastic Multi-Site Downloading",
"version": "0.0.8.2",
"project_urls": null,
"split_keywords": [
"downloading",
"asynchronous",
"multidispatching",
"queueing",
"adaptive",
"elastic",
"adaptilastic",
"federated",
"high-performance"
],
"urls": [
{
"comment_text": "",
"digests": {
"blake2b_256": "64778cb382998d8ef102026068ee4227e96c57f1c33ab388d030f83f8a8a5264",
"md5": "49b16f2cd6e9a8d3fbc480dedb21e20e",
"sha256": "fe6057d1072ecb55936e81feecfe4550d5a391eeee92212c8ab5b3a08f48e0a5"
},
"downloads": -1,
"filename": "flardl-0.0.8.2-py3-none-any.whl",
"has_sig": false,
"md5_digest": "49b16f2cd6e9a8d3fbc480dedb21e20e",
"packagetype": "bdist_wheel",
"python_version": "py3",
"requires_python": "<3.13,>=3.9",
"size": 22399,
"upload_time": "2024-02-02T23:57:53",
"upload_time_iso_8601": "2024-02-02T23:57:53.921875Z",
"url": "https://files.pythonhosted.org/packages/64/77/8cb382998d8ef102026068ee4227e96c57f1c33ab388d030f83f8a8a5264/flardl-0.0.8.2-py3-none-any.whl",
"yanked": false,
"yanked_reason": null
},
{
"comment_text": "",
"digests": {
"blake2b_256": "1990d9d0c5aabbde623c84e58b5aad77af6ded2b3ea42ed126281830db2522d6",
"md5": "7324e76be815d26a0c44cfdd95777cd9",
"sha256": "b1fa82f7e6b5ccc6d31cfe6ca162ff7529369bf6da279ffbd2ab988aef0b0abf"
},
"downloads": -1,
"filename": "flardl-0.0.8.2.tar.gz",
"has_sig": false,
"md5_digest": "7324e76be815d26a0c44cfdd95777cd9",
"packagetype": "sdist",
"python_version": "source",
"requires_python": "<3.13,>=3.9",
"size": 30942,
"upload_time": "2024-02-02T23:57:55",
"upload_time_iso_8601": "2024-02-02T23:57:55.706989Z",
"url": "https://files.pythonhosted.org/packages/19/90/d9d0c5aabbde623c84e58b5aad77af6ded2b3ea42ed126281830db2522d6/flardl-0.0.8.2.tar.gz",
"yanked": false,
"yanked_reason": null
}
],
"upload_time": "2024-02-02 23:57:55",
"github": false,
"gitlab": false,
"bitbucket": false,
"codeberg": false,
"lcname": "flardl"
}