# Gammy – Generalized additive models in Python with a Bayesian twist
A Generalized additive model is a predictive mathematical model defined as a sum
of terms that are calibrated (fitted) with observation data.
Generalized additive models form a surprisingly general framework for building
models for both production software and scientific research. This Python package
offers tools for building the model terms as decompositions of various basis
functions. It is possible to model the terms e.g. as Gaussian processes (with
reduced dimensionality) of various kernels, as piecewise linear functions, and
as B-splines, among others. Of course, very simple terms like lines and
constants are also supported (these are just very simple basis functions).
The uncertainty in the weight parameter distributions is modeled using Bayesian
statistical analysis with the help of the superb package
[BayesPy](http://www.bayespy.org/index.html). Alternatively, it is possible to
fit models using just NumPy.
<!-- markdown-toc start - Don't edit this section. Run M-x markdown-toc-refresh-toc -->
**Table of Contents**
- [Installation](#installation)
- [Examples](#examples)
- [Polynomial regression on 'roids](#polynomial-regression-on-roids)
- [Predicting with model](#predicting-with-model)
- [Plotting results](#plotting-results)
- [Saving model on hard disk](#saving-model-on-hard-disk)
- [Gaussian process regression](#gaussian-process-regression)
- [More covariance kernels](#more-covariance-kernels)
- [Defining custom kernels](#defining-custom-kernels)
- [Spline regression](#spline-regression)
- [Non-linear manifold regression](#non-linear-manifold-regression)
- [Testing](#testing)
- [Package documentation](#package-documentation)
<!-- markdown-toc end -->
## Installation
The package is found in PyPi.
``` shell
pip install gammy
```
## Examples
In this overview, we demonstrate the package's most important features through
common usage examples.
### Polynomial regression on 'roids
A typical simple (but sometimes non-trivial) modeling task is to estimate an
unknown function from noisy data. First we import the bare minimum dependencies to be used in the below examples:
```python
>>> import numpy as np
>>> import gammy
>>> from gammy.models.bayespy import GAM
>>> gammy.__version__
'0.5.3'
```
Let's simulate a dataset:
```python
>>> np.random.seed(42)
>>> n = 30
>>> input_data = 10 * np.random.rand(n)
>>> y = 5 * input_data + 2.0 * input_data ** 2 + 7 + 10 * np.random.randn(n)
```
The object `x` is just a convenience tool for defining input data maps
as if they were just Numpy arrays:
```python
>>> from gammy.arraymapper import x
```
Define and fit the model:
```python
>>> a = gammy.formulae.Scalar(prior=(0, 1e-6))
>>> b = gammy.formulae.Scalar(prior=(0, 1e-6))
>>> bias = gammy.formulae.Scalar(prior=(0, 1e-6))
>>> formula = a * x + b * x ** 2 + bias
>>> model = GAM(formula).fit(input_data, y)
```
The model attribute `model.theta` characterizes the Gaussian posterior
distribution of the model parameters vector.
``` python
>>> model.mean_theta
[array([3.20130444]), array([2.0420961]), array([11.93437195])]
```
Variance of additive zero-mean normally distributed noise is estimated
automagically:
``` python
>>> round(model.inv_mean_tau, 8)
74.51660744
```
#### Predicting with model
```python
>>> model.predict(input_data[:2])
array([ 52.57112684, 226.9460579 ])
```
Predictions with uncertainty, that is, posterior predictive mean and variance
can be calculated as follows:
```python
>>> model.predict_variance(input_data[:2])
(array([ 52.57112684, 226.9460579 ]), array([79.35827362, 95.16358131]))
```
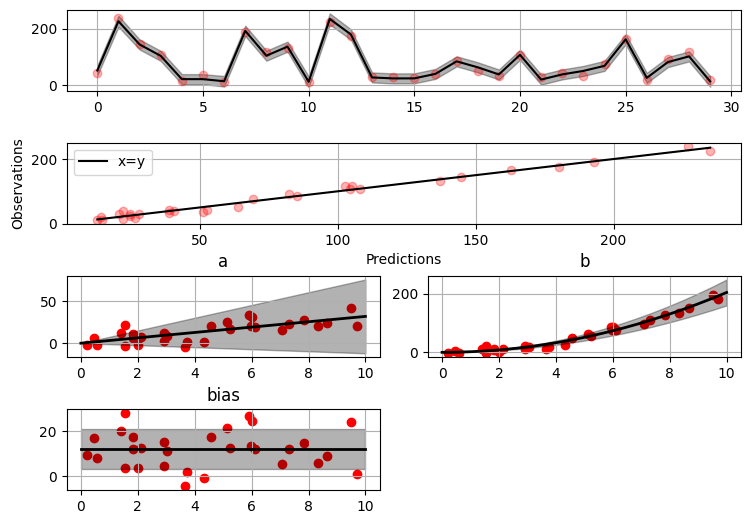
#### Plotting results
```python
>>> fig = gammy.plot.validation_plot(
... model,
... input_data,
... y,
... grid_limits=[0, 10],
... input_maps=[x, x, x],
... titles=["a", "b", "bias"]
... )
```
The grey band in the top figure is two times the prediction standard deviation
and, in the partial residual plots, two times the respective marginal posterior
standard deviation.
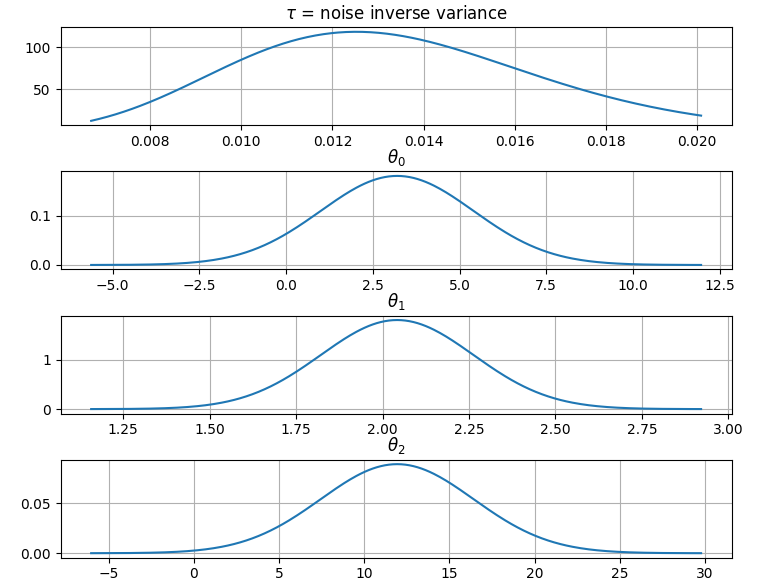
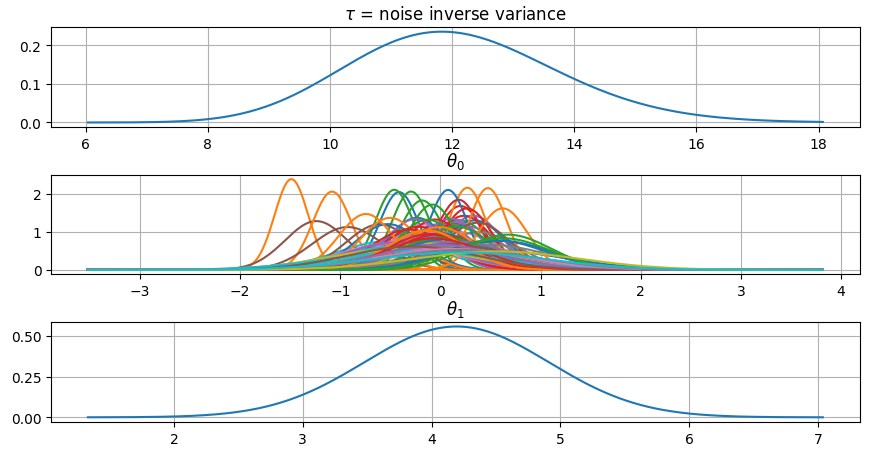
It is also possible to plot the estimated Γ-distribution of the noise precision
(inverse variance) as well as the 1-D Normal distributions of each individual
model parameter.
Plot (prior or posterior) probability density functions of all model parameters:
```python
>>> fig = gammy.plot.gaussian1d_density_plot(model)
```
#### Saving model on hard disk
Saving:
<!-- NOTE: To skip doctests, one > has been removed -->
```python
>> model.save("/home/foobar/test.hdf5")
```
Loading:
<!-- NOTE: To skip doctests, one > has been removed -->
```python
>> model = GAM(formula).load("/home/foobar/test.hdf5")
```
### Gaussian process regression
Create fake dataset:
```python
>>> n = 50
>>> input_data = np.vstack((2 * np.pi * np.random.rand(n), np.random.rand(n))).T
>>> y = (
... np.abs(np.cos(input_data[:, 0])) * input_data[:, 1] +
... 1 + 0.1 * np.random.randn(n)
... )
```
Define model:
``` python
>>> a = gammy.formulae.ExpSineSquared1d(
... np.arange(0, 2 * np.pi, 0.1),
... corrlen=1.0,
... sigma=1.0,
... period=2 * np.pi,
... energy=0.99
... )
>>> bias = gammy.Scalar(prior=(0, 1e-6))
>>> formula = a(x[:, 0]) * x[:, 1] + bias
>>> model = gammy.models.bayespy.GAM(formula).fit(input_data, y)
>>> round(model.mean_theta[0][0], 8)
-0.8343458
```
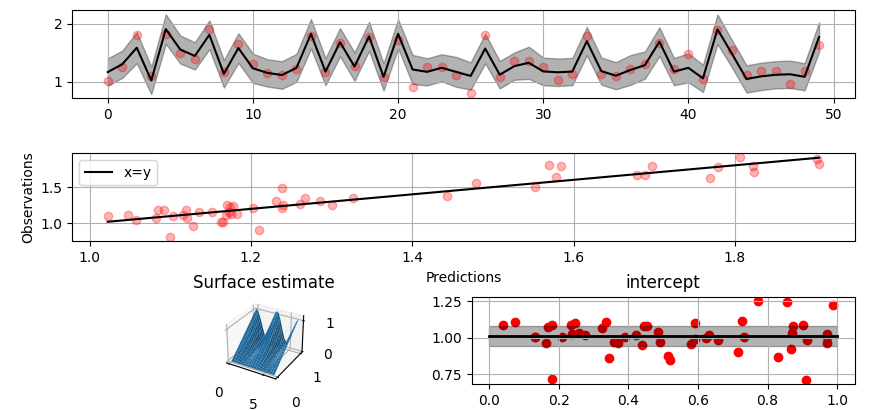
Plot predictions and partial residuals:
``` python
>>> fig = gammy.plot.validation_plot(
... model,
... input_data,
... y,
... grid_limits=[[0, 2 * np.pi], [0, 1]],
... input_maps=[x[:, 0:2], x[:, 1]],
... titles=["Surface estimate", "intercept"]
... )
```
Plot parameter probability density functions
``` python
>>> fig = gammy.plot.gaussian1d_density_plot(model)
```
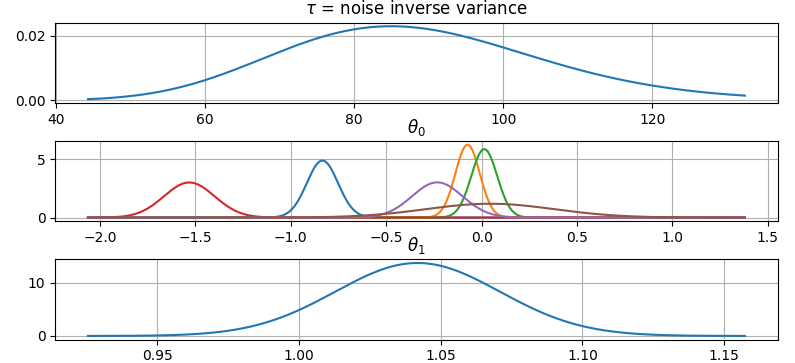
#### More covariance kernels
The package contains covariance functions for many well-known options such as
the _Exponential squared_, _Periodic exponential squared_, _Rational quadratic_,
and the _Ornstein-Uhlenbeck_ kernels. Please see the documentation section [More
on Gaussian Process
kernels](https://malmgrek.github.io/gammy/features.html#more-on-gaussian-process-kernels)
for a gallery of kernels.
#### Defining custom kernels
Please read the documentation section: [Customize Gaussian Process
kernels](https://malmgrek.github.io/gammy/features.html#customize-gaussian-process-kernels)
### Spline regression
Constructing B-Spline based 1-D basis functions is also supported. Let's define
dummy data:
```python
>>> n = 30
>>> input_data = 10 * np.random.rand(n)
>>> y = 2.0 * input_data ** 2 + 7 + 10 * np.random.randn(n)
```
Define model:
``` python
>>> grid = np.arange(0, 11, 2.0)
>>> order = 2
>>> N = len(grid) + order - 2
>>> sigma = 10 ** 2
>>> formula = gammy.BSpline1d(
... grid,
... order=order,
... prior=(np.zeros(N), np.identity(N) / sigma),
... extrapolate=True
... )(x)
>>> model = gammy.models.bayespy.GAM(formula).fit(input_data, y)
>>> round(model.mean_theta[0][0], 8)
-49.00019115
```
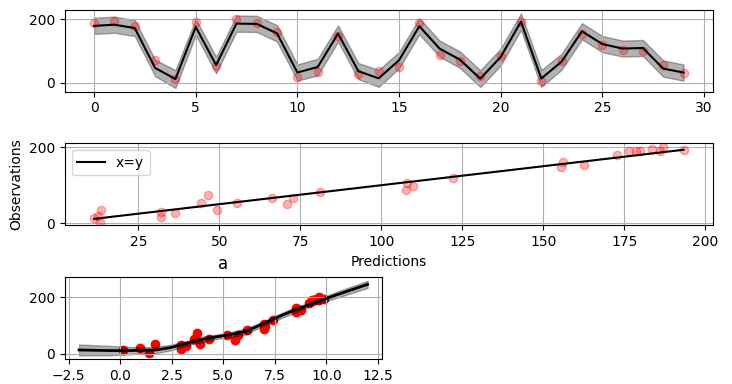
Plot validation figure:
``` python
>>> fig = gammy.plot.validation_plot(
... model,
... input_data,
... y,
... grid_limits=[-2, 12],
... input_maps=[x],
... titles=["a"]
... )
```
Plot parameter probability densities:
``` python
>>> fig = gammy.plot.gaussian1d_density_plot(model)
```
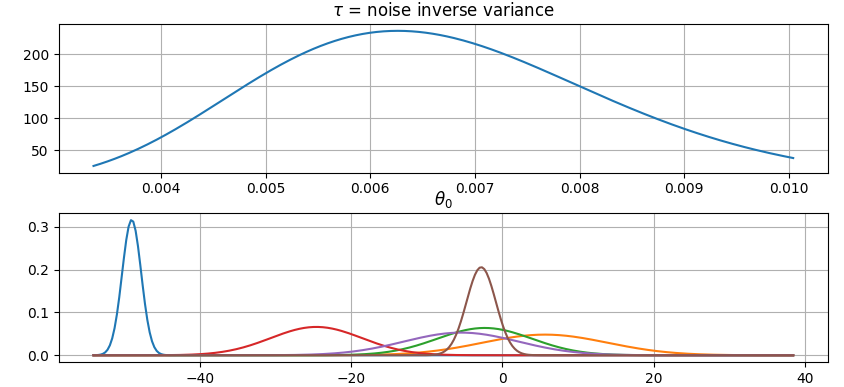
### Non-linear manifold regression
In this example we try estimating the bivariate "MATLAB function" using a
Gaussian process model with Kronecker tensor structure (see e.g.
[PyMC3](https://docs.pymc.io/en/v3/pymc-examples/examples/gaussian_processes/GP-Kron.html)). The main point in the
below example is that it is quite straightforward to build models that can learn
arbitrary 2D-surfaces.
Let us first create some artificial data using the MATLAB function!
```python
>>> n = 100
>>> input_data = np.vstack((
... 6 * np.random.rand(n) - 3, 6 * np.random.rand(n) - 3
... )).T
>>> y = (
... gammy.utils.peaks(input_data[:, 0], input_data[:, 1]) +
... 4 + 0.3 * np.random.randn(n)
... )
```
There is support for forming two-dimensional basis functions given two
one-dimensional formulas. The new combined basis is essentially the outer
product of the given bases. The underlying weight prior distribution priors and
covariances are constructed using the Kronecker product.
```python
>>> a = gammy.ExpSquared1d(
... np.arange(-3, 3, 0.1),
... corrlen=0.5,
... sigma=4.0,
... energy=0.99
... )(x[:, 0]) # NOTE: Input map is defined here!
>>> b = gammy.ExpSquared1d(
... np.arange(-3, 3, 0.1),
... corrlen=0.5,
... sigma=4.0,
... energy=0.99
... )(x[:, 1]) # NOTE: Input map is defined here!
>>> A = gammy.formulae.Kron(a, b)
>>> bias = gammy.formulae.Scalar(prior=(0, 1e-6))
>>> formula = A + bias
>>> model = GAM(formula).fit(input_data, y)
>>> round(model.mean_theta[0][0], 8)
0.37426986
```
Note that same logic could be used to construct higher dimensional bases,
that is, one could define a 3D-formula:
<!-- NOTE: To skip doctests, one > has been removed -->
```python
>> formula_3d = gammy.Kron(gammy.Kron(a, b), c)
```
Plot predictions and partial residuals:
```python
>>> fig = gammy.plot.validation_plot(
... model,
... input_data,
... y,
... grid_limits=[[-3, 3], [-3, 3]],
... input_maps=[x, x[:, 0]],
... titles=["Surface estimate", "intercept"]
... )
```
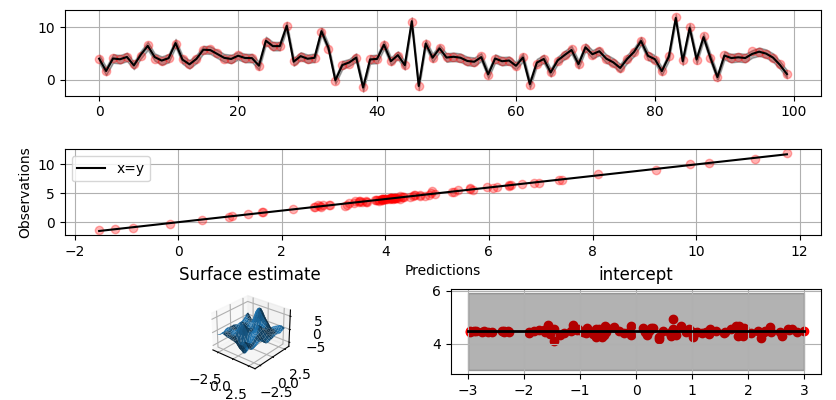
Plot parameter probability density functions:
```
>>> fig = gammy.plot.gaussian1d_density_plot(model)
```
## Testing
The package's unit tests can be ran with PyTest (`cd` to repository root):
``` shell
pytest -v
```
Running this documentation as a Doctest:
``` shell
python -m doctest -v README.md
```
## Package documentation
Documentation of the package with code examples:
<https://malmgrek.github.io/gammy>.
Raw data
{
"_id": null,
"home_page": "https://malmgrek.github.io/gammy",
"name": "gammy",
"maintainer": "Stratos Staboulis <stratos@stratokraft.fi>",
"docs_url": null,
"requires_python": "",
"maintainer_email": "",
"keywords": "bayesian,statistics,modeling,gaussian processes,splines",
"author": "Stratos Staboulis <stratos@stratokraft.fi>",
"author_email": "",
"download_url": "https://files.pythonhosted.org/packages/eb/a7/f1e683d080952fd4b721e93e426a83704ca168f8659a6d940c8869e3dced/gammy-0.5.3.tar.gz",
"platform": null,
"description": "# Gammy \u2013 Generalized additive models in Python with a Bayesian twist\n\n\n\nA Generalized additive model is a predictive mathematical model defined as a sum\nof terms that are calibrated (fitted) with observation data.\n\nGeneralized additive models form a surprisingly general framework for building\nmodels for both production software and scientific research. This Python package\noffers tools for building the model terms as decompositions of various basis\nfunctions. It is possible to model the terms e.g. as Gaussian processes (with\nreduced dimensionality) of various kernels, as piecewise linear functions, and\nas B-splines, among others. Of course, very simple terms like lines and\nconstants are also supported (these are just very simple basis functions).\n\nThe uncertainty in the weight parameter distributions is modeled using Bayesian\nstatistical analysis with the help of the superb package\n[BayesPy](http://www.bayespy.org/index.html). Alternatively, it is possible to\nfit models using just NumPy.\n\n<!-- markdown-toc start - Don't edit this section. Run M-x markdown-toc-refresh-toc -->\n**Table of Contents**\n\n- [Installation](#installation)\n- [Examples](#examples)\n - [Polynomial regression on 'roids](#polynomial-regression-on-roids)\n - [Predicting with model](#predicting-with-model)\n - [Plotting results](#plotting-results)\n - [Saving model on hard disk](#saving-model-on-hard-disk)\n - [Gaussian process regression](#gaussian-process-regression)\n - [More covariance kernels](#more-covariance-kernels)\n - [Defining custom kernels](#defining-custom-kernels)\n - [Spline regression](#spline-regression)\n - [Non-linear manifold regression](#non-linear-manifold-regression)\n- [Testing](#testing)\n- [Package documentation](#package-documentation)\n\n<!-- markdown-toc end -->\n\n## Installation\n\nThe package is found in PyPi.\n\n``` shell\npip install gammy\n```\n\n## Examples\n\nIn this overview, we demonstrate the package's most important features through\ncommon usage examples.\n\n### Polynomial regression on 'roids\n\nA typical simple (but sometimes non-trivial) modeling task is to estimate an\nunknown function from noisy data. First we import the bare minimum dependencies to be used in the below examples:\n\n```python\n>>> import numpy as np\n\n>>> import gammy\n>>> from gammy.models.bayespy import GAM\n\n>>> gammy.__version__\n'0.5.3'\n\n```\n\nLet's simulate a dataset:\n\n```python\n>>> np.random.seed(42)\n\n>>> n = 30\n>>> input_data = 10 * np.random.rand(n)\n>>> y = 5 * input_data + 2.0 * input_data ** 2 + 7 + 10 * np.random.randn(n)\n\n```\n\nThe object `x` is just a convenience tool for defining input data maps\nas if they were just Numpy arrays:\n\n```python\n>>> from gammy.arraymapper import x\n\n```\n\nDefine and fit the model:\n\n```python\n>>> a = gammy.formulae.Scalar(prior=(0, 1e-6))\n>>> b = gammy.formulae.Scalar(prior=(0, 1e-6))\n>>> bias = gammy.formulae.Scalar(prior=(0, 1e-6))\n>>> formula = a * x + b * x ** 2 + bias\n>>> model = GAM(formula).fit(input_data, y)\n\n```\n\nThe model attribute `model.theta` characterizes the Gaussian posterior\ndistribution of the model parameters vector.\n\n``` python\n>>> model.mean_theta\n[array([3.20130444]), array([2.0420961]), array([11.93437195])]\n\n```\n\nVariance of additive zero-mean normally distributed noise is estimated\nautomagically:\n\n``` python\n>>> round(model.inv_mean_tau, 8)\n74.51660744\n\n```\n\n#### Predicting with model\n\n```python\n>>> model.predict(input_data[:2])\narray([ 52.57112684, 226.9460579 ])\n\n```\n\nPredictions with uncertainty, that is, posterior predictive mean and variance\ncan be calculated as follows:\n\n```python\n>>> model.predict_variance(input_data[:2])\n(array([ 52.57112684, 226.9460579 ]), array([79.35827362, 95.16358131]))\n\n```\n\n#### Plotting results\n\n```python\n>>> fig = gammy.plot.validation_plot(\n... model,\n... input_data,\n... y,\n... grid_limits=[0, 10],\n... input_maps=[x, x, x],\n... titles=[\"a\", \"b\", \"bias\"]\n... )\n\n```\n\nThe grey band in the top figure is two times the prediction standard deviation\nand, in the partial residual plots, two times the respective marginal posterior\nstandard deviation.\n\n\n\nIt is also possible to plot the estimated \u0393-distribution of the noise precision\n(inverse variance) as well as the 1-D Normal distributions of each individual\nmodel parameter.\n\nPlot (prior or posterior) probability density functions of all model parameters:\n\n```python\n>>> fig = gammy.plot.gaussian1d_density_plot(model)\n\n```\n\n\n\n#### Saving model on hard disk\n\nSaving:\n\n<!-- NOTE: To skip doctests, one > has been removed -->\n```python\n>> model.save(\"/home/foobar/test.hdf5\")\n```\n\nLoading:\n\n<!-- NOTE: To skip doctests, one > has been removed -->\n```python\n>> model = GAM(formula).load(\"/home/foobar/test.hdf5\")\n```\n\n### Gaussian process regression\n\nCreate fake dataset:\n\n```python\n>>> n = 50\n>>> input_data = np.vstack((2 * np.pi * np.random.rand(n), np.random.rand(n))).T\n>>> y = (\n... np.abs(np.cos(input_data[:, 0])) * input_data[:, 1] +\n... 1 + 0.1 * np.random.randn(n)\n... )\n\n```\n\nDefine model:\n\n``` python\n>>> a = gammy.formulae.ExpSineSquared1d(\n... np.arange(0, 2 * np.pi, 0.1),\n... corrlen=1.0,\n... sigma=1.0,\n... period=2 * np.pi,\n... energy=0.99\n... )\n>>> bias = gammy.Scalar(prior=(0, 1e-6))\n>>> formula = a(x[:, 0]) * x[:, 1] + bias\n>>> model = gammy.models.bayespy.GAM(formula).fit(input_data, y)\n\n>>> round(model.mean_theta[0][0], 8)\n-0.8343458\n\n```\n\nPlot predictions and partial residuals:\n\n``` python\n>>> fig = gammy.plot.validation_plot(\n... model,\n... input_data,\n... y,\n... grid_limits=[[0, 2 * np.pi], [0, 1]],\n... input_maps=[x[:, 0:2], x[:, 1]],\n... titles=[\"Surface estimate\", \"intercept\"]\n... )\n\n```\n\n\n\nPlot parameter probability density functions\n\n``` python\n>>> fig = gammy.plot.gaussian1d_density_plot(model)\n\n```\n\n\n\n#### More covariance kernels\n\nThe package contains covariance functions for many well-known options such as\nthe _Exponential squared_, _Periodic exponential squared_, _Rational quadratic_,\nand the _Ornstein-Uhlenbeck_ kernels. Please see the documentation section [More\non Gaussian Process\nkernels](https://malmgrek.github.io/gammy/features.html#more-on-gaussian-process-kernels)\nfor a gallery of kernels.\n\n#### Defining custom kernels\n\nPlease read the documentation section: [Customize Gaussian Process\nkernels](https://malmgrek.github.io/gammy/features.html#customize-gaussian-process-kernels)\n\n### Spline regression\n\nConstructing B-Spline based 1-D basis functions is also supported. Let's define\ndummy data:\n\n```python\n>>> n = 30\n>>> input_data = 10 * np.random.rand(n)\n>>> y = 2.0 * input_data ** 2 + 7 + 10 * np.random.randn(n)\n\n```\n\nDefine model:\n\n``` python\n>>> grid = np.arange(0, 11, 2.0)\n>>> order = 2\n>>> N = len(grid) + order - 2\n>>> sigma = 10 ** 2\n>>> formula = gammy.BSpline1d(\n... grid,\n... order=order,\n... prior=(np.zeros(N), np.identity(N) / sigma),\n... extrapolate=True\n... )(x)\n>>> model = gammy.models.bayespy.GAM(formula).fit(input_data, y)\n\n>>> round(model.mean_theta[0][0], 8)\n-49.00019115\n\n```\n\nPlot validation figure:\n\n``` python\n>>> fig = gammy.plot.validation_plot(\n... model,\n... input_data,\n... y,\n... grid_limits=[-2, 12],\n... input_maps=[x],\n... titles=[\"a\"]\n... )\n\n```\n\n\n\nPlot parameter probability densities:\n\n ``` python\n>>> fig = gammy.plot.gaussian1d_density_plot(model)\n\n ```\n\n\n\n### Non-linear manifold regression\n\nIn this example we try estimating the bivariate \"MATLAB function\" using a\nGaussian process model with Kronecker tensor structure (see e.g.\n[PyMC3](https://docs.pymc.io/en/v3/pymc-examples/examples/gaussian_processes/GP-Kron.html)). The main point in the\nbelow example is that it is quite straightforward to build models that can learn\narbitrary 2D-surfaces.\n\nLet us first create some artificial data using the MATLAB function!\n\n```python\n>>> n = 100\n>>> input_data = np.vstack((\n... 6 * np.random.rand(n) - 3, 6 * np.random.rand(n) - 3\n... )).T\n>>> y = (\n... gammy.utils.peaks(input_data[:, 0], input_data[:, 1]) +\n... 4 + 0.3 * np.random.randn(n)\n... )\n\n```\n\nThere is support for forming two-dimensional basis functions given two\none-dimensional formulas. The new combined basis is essentially the outer\nproduct of the given bases. The underlying weight prior distribution priors and\ncovariances are constructed using the Kronecker product.\n\n```python\n>>> a = gammy.ExpSquared1d(\n... np.arange(-3, 3, 0.1),\n... corrlen=0.5,\n... sigma=4.0,\n... energy=0.99\n... )(x[:, 0]) # NOTE: Input map is defined here!\n>>> b = gammy.ExpSquared1d(\n... np.arange(-3, 3, 0.1),\n... corrlen=0.5,\n... sigma=4.0,\n... energy=0.99\n... )(x[:, 1]) # NOTE: Input map is defined here!\n>>> A = gammy.formulae.Kron(a, b)\n>>> bias = gammy.formulae.Scalar(prior=(0, 1e-6))\n>>> formula = A + bias\n>>> model = GAM(formula).fit(input_data, y)\n\n>>> round(model.mean_theta[0][0], 8)\n0.37426986\n\n```\n\nNote that same logic could be used to construct higher dimensional bases,\nthat is, one could define a 3D-formula:\n\n<!-- NOTE: To skip doctests, one > has been removed -->\n```python\n>> formula_3d = gammy.Kron(gammy.Kron(a, b), c)\n\n```\n\nPlot predictions and partial residuals:\n\n```python\n>>> fig = gammy.plot.validation_plot(\n... model,\n... input_data,\n... y,\n... grid_limits=[[-3, 3], [-3, 3]],\n... input_maps=[x, x[:, 0]],\n... titles=[\"Surface estimate\", \"intercept\"]\n... )\n\n```\n\n\n\nPlot parameter probability density functions:\n\n```\n>>> fig = gammy.plot.gaussian1d_density_plot(model)\n\n```\n\n\n\n## Testing\n\nThe package's unit tests can be ran with PyTest (`cd` to repository root):\n\n``` shell\npytest -v\n```\n\nRunning this documentation as a Doctest:\n\n``` shell\npython -m doctest -v README.md\n```\n\n## Package documentation\n\nDocumentation of the package with code examples:\n<https://malmgrek.github.io/gammy>.\n",
"bugtrack_url": null,
"license": "MIT",
"summary": "Generalized additive models with a Bayesian twist",
"version": "0.5.3",
"project_urls": {
"Homepage": "https://malmgrek.github.io/gammy"
},
"split_keywords": [
"bayesian",
"statistics",
"modeling",
"gaussian processes",
"splines"
],
"urls": [
{
"comment_text": "",
"digests": {
"blake2b_256": "eaff2b0d9004ede21f5c4e6a8ebf4b60dc901b2b75a53817c10101975ec735e3",
"md5": "d36700d80719097169f4195f86cad14c",
"sha256": "c06b952afdc8a1975ce0f77c934f5b6ce4bd04df95a95421b3c73b54e8f44667"
},
"downloads": -1,
"filename": "gammy-0.5.3-py3-none-any.whl",
"has_sig": false,
"md5_digest": "d36700d80719097169f4195f86cad14c",
"packagetype": "bdist_wheel",
"python_version": "py3",
"requires_python": null,
"size": 23947,
"upload_time": "2024-01-02T10:51:13",
"upload_time_iso_8601": "2024-01-02T10:51:13.388046Z",
"url": "https://files.pythonhosted.org/packages/ea/ff/2b0d9004ede21f5c4e6a8ebf4b60dc901b2b75a53817c10101975ec735e3/gammy-0.5.3-py3-none-any.whl",
"yanked": false,
"yanked_reason": null
},
{
"comment_text": "",
"digests": {
"blake2b_256": "eba7f1e683d080952fd4b721e93e426a83704ca168f8659a6d940c8869e3dced",
"md5": "8a0d47135be211bfb85bf081c89a94b0",
"sha256": "dbec1da96c8667a642d0aad39749613891452d059a47fc4c6ba6593e52d733f0"
},
"downloads": -1,
"filename": "gammy-0.5.3.tar.gz",
"has_sig": false,
"md5_digest": "8a0d47135be211bfb85bf081c89a94b0",
"packagetype": "sdist",
"python_version": "source",
"requires_python": null,
"size": 33800,
"upload_time": "2024-01-02T10:51:15",
"upload_time_iso_8601": "2024-01-02T10:51:15.297886Z",
"url": "https://files.pythonhosted.org/packages/eb/a7/f1e683d080952fd4b721e93e426a83704ca168f8659a6d940c8869e3dced/gammy-0.5.3.tar.gz",
"yanked": false,
"yanked_reason": null
}
],
"upload_time": "2024-01-02 10:51:15",
"github": false,
"gitlab": false,
"bitbucket": false,
"codeberg": false,
"lcname": "gammy"
}