| Name | hngd JSON |
| Version |
1.0.1
 JSON
JSON |
| download |
| home_page | |
| Summary | Implementation of the Hydride Nucleation-Growth-Dissolution (HNGD) model. Simulates hydrogen behaviour in a 1D geometry using an explicit finite difference scheme (Euler method). |
| upload_time | 2023-09-18 19:55:40 |
| maintainer | |
| docs_url | None |
| author | |
| requires_python | >=3.10 |
| license | BSD-3-Clause |
| keywords |
hngd
hydrogen
hydrides
nuclear fuel cladding
diffusion
|
| VCS |
|
| bugtrack_url |
|
| requirements |
No requirements were recorded.
|
| Travis-CI |
No Travis.
|
| coveralls test coverage |
No coveralls.
|
# HNGD-Model
A package with an implementation of the Hydride Nucleation-Growth-Dissolution
(HNGD) model, that simulates hydrogen behaviour in Zirconium alloys in a 1D geometry using an explicit finite difference scheme (Euler method).
## Installation
It is highly recommended that you install this package in an isolated virtual environment. If you are using [Anaconda](https://conda.io/projects/conda/en/latest/user-guide/tasks/manage-environments.html), open Anaconda Prompt and create the environment `HNGD-env` with the latest Python version:
```
conda create --name HNGD-env python
```
Then, activate this environment:
```
conda activate HNGD-env
```
And install the package as:
```
pip install hngd
```
If you are not using Anaconda, you can use a similar procedure with the [venv module](https://docs.python.org/3/library/venv.html).
### For developers
If you want an [editable version](https://setuptools.pypa.io/en/latest/userguide/development_mode.html) of the code (i. e. a version for developers), clone this repository to the desired location, move to that directory (`cd C:\path\to\install\HNGD-Model`) and install the package as:
```
pip install -e .
```
## How to use
### Input parameters
In order to do a simulation, there are five obligatory inputs needed:
- Experimental data
- Simulation data
- Thermal history
- Initial hydrogen concentration
- Model parameters
The following sections explains each of these input parameters in detail.
#### 1. Experimental data
Data from the experiment. Consists on a tuple with the following information:
```
experimental_data = (slab length [m] -> float,
flux at the left of the sample [wt.ppm m-2 s-1] -> float,
flux at the left of the sample [wt.ppm m-2 s-1] -> float,
liner solubility factor [/] -> float,
liner width [m] -> float)
```
A liner is a thin, protective layer that is sometimes applied to the inner surface of the cladding. In the model, it is implemented through a local difference in solubility: liners are usually made of pure Zr and don't have much oxygen, causing the solubility in the liner to be lower than in the rest of the cladding. This difference in solubility is given by the liner solubility factor, and typical values range between 0.95-0.98.
For example:
```python
experimental_data = (0.025, 0, 0, 1, 0)
```
Corresponds to a slab with a length of 2.5 cm, with no hydrogen flux coming to the sample, and no liner.
#### 2. Simulation data
Data from the simulation. Consists on a tuple with the following information:
```
simulation_data = (name -> str,
number of nodes -> int,
dt_div -> float,
test_t_set [s] -> float,
output_criterion -> float,
model -> str)
```
The `name` is used to name output files. The `number of nodes` corresponds to the 1-D spatial discretization. The time step obtained to ensure a stable solution for the forward Euler method can be divided by `dt_div` to produce a more accurate solution. Because time steps can be quite small, the solution is not saved at every time iteration. An output will be saved if `test_t_set` seconds have passed, or if the average relative difference between the current and last temperature or hydrogen concentration profile is greater than the `output_criterion` (for example, a value of 0.01 correspond to a 1% change between the current and last temperature/concentration profile). The `model` represent which model is used for the simulation: the original HNGD model or the modified mHNGD model.
For example:
```python
simulation_data = ('test', 70, 2, 80, 0.01, 'mHNGD')
```
Corresponds to a 70-node discretization, where the stable time step is divided by 2, and the output will be saved every 80 seconds, or if the temperature or hydrogen profiles changed more than 1% with respect to the last time step, and the simulation is run using the mHNGD model.
#### 3. Thermal history
Thermal treatment applied to the sample. Consists on a `numpy` array with the following shape:
```
temperature_data = np.array([[np.nan, pos_1 , pos_2 , ... , pos_n ],
[time_1, temp_1_1, temp_2_1, ... , temp_n_1],
[time_2, temp_1_2, temp_2_2, ... , temp_n_2],
[time_3, temp_1_3, temp_2_3, ... , temp_n_3],
[ ... , ... , ... , ... , ... ],
[time_k, temp_1_k, temp_2_k, ... , temp_n_k]])
```
The first row corresponds to the positions at which the temperature is defined [m]. The first column corresponds the different time stamps at which the temperature is defined [minutes]. The temperature at each position and time stamp is given in [°C]. Temperatures at intermediate positions and time stamps are obtained by linear interpolation.
For example:
```python
temperature_data = np.array([[np.nan, 0, 0.025/2, 0.025],
[ 0, 20, 50, 20],
[ 38, 400, 200, 400],
[ 48, 400, 400, 400],
[ 68, 400, 400, 400],
[ 108, 20, 80, 20]])
```
Corresponds to an initial temperature profile given by 20°C at the edges of the sample, and 50°C at the middle of the sample. Then, after 38 minutes the temperature increased to 400°C at the edges of the sample, and 200°C at the center. Ten minutes later, the temperature profile is uniform, at 400°C, and it is maintained for 20 minutes. Then, at 108 minutes the temperature is 20°C at the edges and 80°C at the middle.
An animation of this sample thermal treatment would be:
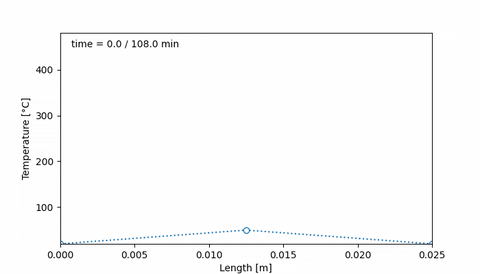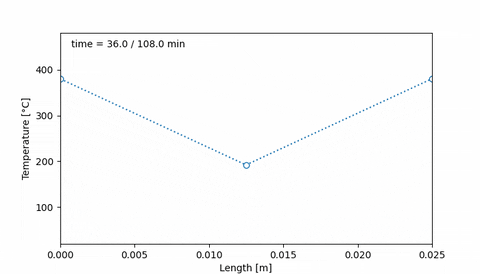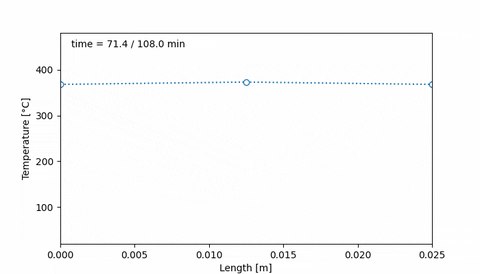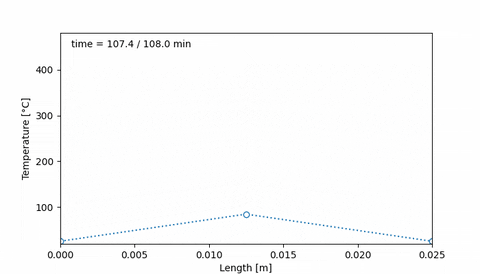
#### 4. Initial hydrogen concentration
The hydrogen profile at the start of the experiment. Consists on a `numpy` array with the following shape:
```
initial_hydrogen_data = np.array([[pos_1, pos_2, pos_3, ..., pos_n],,
[hyd_1, hyd_2, hyd_3, ..., hyd_n]])
```
The first row corresponds to the positions at which the hydrogen concentration is defined [m]. The second row corresponds to the hydrogen concentration at each of these positions [wt.ppm]. Concentration at intermediate positions are obtained by linear interpolation.
For example:
```python
initial_hydrogen_data = np.array([[ 0, 0.025],
[205, 205]])
```
Corresponds to a uniform initial hydrogen profile of 205 wt.ppm.
#### 5. Model parameters
The HNGD model has a large number of parameters regarding Hydrogen solubility and diffusion, formation energy of hydrides, kinetics of nucleation, growth and dissolution, etc. Default model parameters can be imported and used as:
```python
import hngd.default
model_parameters = hngd.default.model_parameters
```
Then, `model_parameters` is a Python dictionary with the following keys and values:
- 'TSSd0': Pre-exponential term for TSSd [wt pmm] = 102000
- 'Q_TSSd': Activation energy for TSSd [J mol-1] = 35458.7
- 'TSSp0': Pre-exponential term for TSSp [wt ppm] = 30853.3
- 'Q_TSSp': Activation energy for TSSp [J mol-1] = 25249.6
- 'D0': Pre-exponential term of the diffusion coefficient [m2 s-1] = 1.08e-6
- 'Ed': Activation energy of the diffusion coefficient [eV at-1] = 0.46
- 'Q_star': Heat of transport of hydrogen in zirconium [J mol-1] = 25500
- 'V_star': Partial molar volume of hydrogen in the zirconium matrix [m3 mol-1] = 1.7e-6
- 'Eg': Activation energy for diffusion driven growth [eV at-1] = 0.9
- 'avrami_parameter': Avrami parameter for platelets [/] = 2.5
- 'Eth0': 0th coefficient of formation energy polynomial [eV at-1] = 0.5655
- 'Eth1': 1st coefficient of formation energy polynomial [eV at-1 K-1] = 4.0e-4
- 'Eth2': 2nd coefficient of formation energy polynomial [eV at-1 K-2] = 2.0e-7
- 'Eth3': 3rd coefficient of formation energy polynomial [eV at-1 K-3] = 3.0e-10
- 'K_G_mob0': Pre-exponential factor for diffusion-controlled growth [s-1] = 5.53e5
- 'K_G_th0': Pre-exponential factor for reaction-controlled growth [s-1] = 1.6e-5
- 'K_N_0': Pre-exponential factor for nucleation kinetics [s-1] = 2.75e-5
- 'K_D_0': Pre-exponential factor for dissolution kinetics [s-1] = 1110.13
- 'tau': tau for mHNGD [s] = 1e4
- 'g': g for mHNGD [wt.ppm] = 120
- 'delta': delta for mHNGD [/] = 1.05
Default model parameters can be modified. For example, to change the default diffusion coefficient given by [Zhang et al.](https://www.nature.com/articles/srep41033) to the one given by [Kearns](https://doi.org/10.1016/0022-3115(72)90065-7), the corresponding parameters can be changed as:
```python
model_parameters['D0'] = 7.90e-7
model_parameters['Ed'] = 0.47
```
### Running a simulation
In order to run a simulation, the `hngd.run` module is imported. Then, set up the input parameters described in the previous section, and use the `simulation` function as:
```python
import hngd.run
import hngd.default
import numpy as np
experiment_data = (0.025, 0, 0, 1, 0)
simulation_data = ('test', 70, 2, 80, 0.01, 'mHNGD')
temperature_data = np.array([[np.nan, 0, experiment_data[0]],
[ 0, 20, 20],
[ 38, 400, 400],
[ 48, 400, 400],
[ 86, 20, 20]])
initial_hydrogen_data = np.array([[ 0, experiment_data[0]],
[205, 205]])
model_parameters = hngd.default.model_parameters
hngd.run.simulation(temperature_data, initial_hydrogen_data, experiment_data,
simulation_data, model_parameters)
```
After the simulation is completed, the results will be saved in a txt file which contains the time, temperature, fraction of precipitation due to growth, fraction of precipitation due to nucleation, hydrogen concentration in solid solution and hydrogen concentration in hydrides.
There are additional optional parameters for the simulation function:
- `node`: Change for which node of the spatial discretization the results are saved. Defaults to 1 (node at the left of the sample).
- `save_results`: If you want to save the results in a txt file. Defaults to True.
- `save_last_concentration_profile`: If you want to save the concentration profile of hydrogen in solid solution and hydrogen in hydrides for the last time step. Useful to compare to some experiments in the literature. Defaults to False.
- `unit_time`: Units of time in the output file, can be 's' (seconds), 'm' (minutes), 'h' (hours) or 'd' (days). Defaults to 's'.
- `unit_temperature`: Units of temperature in the output file, can be 'C' (celsius) or 'K' (kelvin). Defaults to 'K'.
### Running an animation
In order to run an animation, the `hngd.run` module is imported. Then, set up the input parameters described in the previous section, and use the `animation` function as:
```python
import numpy as np
import hngd.default_model_parameters
import hngd.run
experiment_data = (0.025, 0, 0, 1, 0)
simulation_data = ('test', 70, 2, 40, 0.01, 'mHNGD')
temperature_data = np.array([[np.nan, 0, experiment_data[0]],
[ 0, 20, 20],
[ 38, 400, 400],
[ 48, 400, 400],
[ 86, 20, 20]])
initial_hydrogen_data = np.array([[ 0, experiment_data[0]],
[205, 205]])
model_parameters = hngd.default_model_parameters.model_parameters
animation = hngd.run.animation(temperature_data, initial_hydrogen_data,
experiment_data, simulation_data, model_parameters)
```
The animation shows four plots: the evolution of the hydrogen profile (top, left), the evolution of the temperature profile (top, right), the evolution of hydrogen in solid solution as a function of temperature at a single node (bottom, left), and the evolution of temperature as a function of time at a single node (bottom, right).
There are additional optional parameters for the animation function:
- `node`: Which node is used to animate the temporal evolution. Defaults to the node at the middle of the sample (i. e., `simulation_data[1]//2`).
- `save_animation`: If you want to save the animation as a gif. Defaults to False. *Note: When `save_animation=True`, the animation will not be displayed (to fix!).*
- `interval`: Delay between frames in milliseconds. Defaults to 5.
- `repeat`: Whether the animation repeats when the sequence of frames is completed. Defaults to False. *Note: Currently not working (to fix!).*
### Others
There are several other possibilities of the code, such as running a time-temperature-transformation experiment (TTT diagram) using `hngd.run.TTT`, or using `hngd.run.debugger` if you are a developer and want to modify the source code and need a debugger. Some of these applications can be found in the Examples folder of this repository.
## Note for Developers
This code uses the open source, just-in-time (JIT) compiler from the [numba](https://numba.pydata.org/) library, which translates Python functions to optimized machine code at runtime using the industry-standard LLVM compiler library.
If you are making changes to the code and want to use the debugger to do some testing, you will have to disable numba. This can be done by setting:
```
DISABLE_JIT: True
```
in the `.numba_config.yaml` file which is located at the `hngd` folder.
## References
Some references for the HNGD model:
[1] Lacroix E., *Modeling zirconium hydride precipitation and dissolution in zirconium alloys*, PhD Thesis, The Pennsylvania State University (2019).
[2] Passelaigue F., *Hydride Nucleation-Growth-Dissolution model: Implementation in BISON*, MSc. Thesis, The Pennsylvania State University (2020).
[3] Passelaigue F., Lacroix E., Pastore G. and Motta A. T., *Implementation and validation of the Hydride Nucleation-Growth-Dissolution (HNGD) model in BISON*, Journal of Nuclear Materials 544, pp. 152683 (2021). [https://doi.org/10.1016/j.jnucmat.2020.152683](https://doi.org/10.1016/j.jnucmat.2020.152683).
[4] Passelaigue F., Simon, P. A. and Motta, A. T., *Predicting the hydride rim by improving the solubility limits in the Hydride Nucleation-Growth-Dissolution (HNGD) model*, Journal of Nuclear Materials 558, pp. 153363 (2022). [https://doi.org/10.1016/j.jnucmat.2021.153363](https://doi.org/10.1016/j.jnucmat.2021.153363).
[5] Bin Seo S., Duchnowski E. M., Motta A. T., Kammenzind B. F. and Brown N. R.,*Sensitivity analysis for characterizing the impact of HNGD model on the prediction of hydrogen redistribution in Zircaloy cladding using BISON code*, Nuclear Engineering and Design 393, pp. 111813 (2022). [https://doi.org/10.1016/j.nucengdes.2022.111813](https://doi.org/10.1016/j.nucengdes.2022.111813).
[6] Lee C. and Lee, Y., *Simulation of hydrogen diffusion along the axial direction in zirconium cladding tube during dry storage*, Journal of Nuclear Materials 579, pp. 154352 (2023). [https://doi.org/10.1016/j.jnucmat.2023.154352](https://doi.org/10.1016/j.jnucmat.2023.154352)
Raw data
{
"_id": null,
"home_page": "",
"name": "hngd",
"maintainer": "",
"docs_url": null,
"requires_python": ">=3.10",
"maintainer_email": "",
"keywords": "HNGD,Hydrogen,Hydrides,Nuclear fuel cladding,Diffusion",
"author": "",
"author_email": "Francisco Rotea <francisco.rotea@gmail.com>",
"download_url": "https://files.pythonhosted.org/packages/4c/48/f0efbd53c126771d3fc1fd11ac277b995ca90b965fc5c0d1edf24545fe76/hngd-1.0.1.tar.gz",
"platform": null,
"description": "# HNGD-Model\r\n\r\nA package with an implementation of the Hydride Nucleation-Growth-Dissolution\r\n(HNGD) model, that simulates hydrogen behaviour in Zirconium alloys in a 1D geometry using an explicit finite difference scheme (Euler method).\r\n\r\n## Installation\r\n\r\nIt is highly recommended that you install this package in an isolated virtual environment. If you are using [Anaconda](https://conda.io/projects/conda/en/latest/user-guide/tasks/manage-environments.html), open Anaconda Prompt and create the environment `HNGD-env` with the latest Python version:\r\n\r\n```\r\n conda create --name HNGD-env python\r\n```\r\n\r\nThen, activate this environment:\r\n\r\n```\r\n conda activate HNGD-env\r\n```\r\n\r\nAnd install the package as:\r\n\r\n```\r\n pip install hngd\r\n```\r\n\r\nIf you are not using Anaconda, you can use a similar procedure with the [venv module](https://docs.python.org/3/library/venv.html).\r\n\r\n### For developers\r\n\r\nIf you want an [editable version](https://setuptools.pypa.io/en/latest/userguide/development_mode.html) of the code (i. e. a version for developers), clone this repository to the desired location, move to that directory (`cd C:\\path\\to\\install\\HNGD-Model`) and install the package as:\r\n\r\n```\r\n pip install -e .\r\n```\r\n\r\n## How to use\r\n\r\n### Input parameters\r\n\r\nIn order to do a simulation, there are five obligatory inputs needed:\r\n\r\n- Experimental data\r\n- Simulation data\r\n- Thermal history\r\n- Initial hydrogen concentration\r\n- Model parameters\r\n\r\nThe following sections explains each of these input parameters in detail.\r\n\r\n#### 1. Experimental data\r\n\r\nData from the experiment. Consists on a tuple with the following information:\r\n\r\n```\r\nexperimental_data = (slab length [m] -> float, \r\n flux at the left of the sample [wt.ppm m-2 s-1] -> float, \r\n flux at the left of the sample [wt.ppm m-2 s-1] -> float, \r\n liner solubility factor [/] -> float, \r\n liner width [m] -> float)\r\n```\r\n\r\nA liner is a thin, protective layer that is sometimes applied to the inner surface of the cladding. In the model, it is implemented through a local difference in solubility: liners are usually made of pure Zr and don't have much oxygen, causing the solubility in the liner to be lower than in the rest of the cladding. This difference in solubility is given by the liner solubility factor, and typical values range between 0.95-0.98. \r\n \r\nFor example:\r\n\r\n```python\r\nexperimental_data = (0.025, 0, 0, 1, 0) \r\n```\r\n\r\nCorresponds to a slab with a length of 2.5 cm, with no hydrogen flux coming to the sample, and no liner. \r\n\r\n#### 2. Simulation data\r\n\r\nData from the simulation. Consists on a tuple with the following information:\r\n\r\n```\r\nsimulation_data = (name -> str, \r\n number of nodes -> int, \r\n dt_div -> float, \r\n test_t_set [s] -> float, \r\n output_criterion -> float,\r\n model -> str)\r\n```\r\n\r\nThe `name` is used to name output files. The `number of nodes` corresponds to the 1-D spatial discretization. The time step obtained to ensure a stable solution for the forward Euler method can be divided by `dt_div` to produce a more accurate solution. Because time steps can be quite small, the solution is not saved at every time iteration. An output will be saved if `test_t_set` seconds have passed, or if the average relative difference between the current and last temperature or hydrogen concentration profile is greater than the `output_criterion` (for example, a value of 0.01 correspond to a 1% change between the current and last temperature/concentration profile). The `model` represent which model is used for the simulation: the original HNGD model or the modified mHNGD model.\r\n \r\nFor example:\r\n\r\n```python\r\nsimulation_data = ('test', 70, 2, 80, 0.01, 'mHNGD')\r\n```\r\n\r\nCorresponds to a 70-node discretization, where the stable time step is divided by 2, and the output will be saved every 80 seconds, or if the temperature or hydrogen profiles changed more than 1% with respect to the last time step, and the simulation is run using the mHNGD model.\r\n\r\n#### 3. Thermal history\r\n\r\nThermal treatment applied to the sample. Consists on a `numpy` array with the following shape:\r\n\r\n```\r\ntemperature_data = np.array([[np.nan, pos_1 , pos_2 , ... , pos_n ],\r\n [time_1, temp_1_1, temp_2_1, ... , temp_n_1],\r\n [time_2, temp_1_2, temp_2_2, ... , temp_n_2],\r\n [time_3, temp_1_3, temp_2_3, ... , temp_n_3],\r\n [ ... , ... , ... , ... , ... ],\r\n [time_k, temp_1_k, temp_2_k, ... , temp_n_k]])\r\n\r\n```\r\n\r\nThe first row corresponds to the positions at which the temperature is defined [m]. The first column corresponds the different time stamps at which the temperature is defined [minutes]. The temperature at each position and time stamp is given in [\u00b0C]. Temperatures at intermediate positions and time stamps are obtained by linear interpolation.\r\n\r\nFor example:\r\n\r\n```python\r\ntemperature_data = np.array([[np.nan, 0, 0.025/2, 0.025],\r\n [ 0, 20, 50, 20],\r\n [ 38, 400, 200, 400],\r\n [ 48, 400, 400, 400],\r\n [ 68, 400, 400, 400],\r\n [ 108, 20, 80, 20]])\r\n```\r\n\r\nCorresponds to an initial temperature profile given by 20\u00b0C at the edges of the sample, and 50\u00b0C at the middle of the sample. Then, after 38 minutes the temperature increased to 400\u00b0C at the edges of the sample, and 200\u00b0C at the center. Ten minutes later, the temperature profile is uniform, at 400\u00b0C, and it is maintained for 20 minutes. Then, at 108 minutes the temperature is 20\u00b0C at the edges and 80\u00b0C at the middle.\r\n\r\nAn animation of this sample thermal treatment would be:\r\n\r\n\r\n\r\n#### 4. Initial hydrogen concentration\r\n\r\nThe hydrogen profile at the start of the experiment. Consists on a `numpy` array with the following shape:\r\n\r\n```\r\ninitial_hydrogen_data = np.array([[pos_1, pos_2, pos_3, ..., pos_n],,\r\n [hyd_1, hyd_2, hyd_3, ..., hyd_n]])\r\n```\r\n\r\nThe first row corresponds to the positions at which the hydrogen concentration is defined [m]. The second row corresponds to the hydrogen concentration at each of these positions [wt.ppm]. Concentration at intermediate positions are obtained by linear interpolation.\r\n\r\nFor example:\r\n\r\n```python\r\ninitial_hydrogen_data = np.array([[ 0, 0.025],\r\n [205, 205]])\r\n```\r\n\r\nCorresponds to a uniform initial hydrogen profile of 205 wt.ppm.\r\n\r\n#### 5. Model parameters\r\n\r\nThe HNGD model has a large number of parameters regarding Hydrogen solubility and diffusion, formation energy of hydrides, kinetics of nucleation, growth and dissolution, etc. Default model parameters can be imported and used as:\r\n\r\n```python\r\nimport hngd.default\r\n\r\nmodel_parameters = hngd.default.model_parameters\r\n```\r\n\r\nThen, `model_parameters` is a Python dictionary with the following keys and values:\r\n\r\n- 'TSSd0': Pre-exponential term for TSSd [wt pmm] = 102000\r\n- 'Q_TSSd': Activation energy for TSSd [J mol-1] = 35458.7\r\n- 'TSSp0': Pre-exponential term for TSSp [wt ppm] = 30853.3\r\n- 'Q_TSSp': Activation energy for TSSp [J mol-1] = 25249.6\r\n- 'D0': Pre-exponential term of the diffusion coefficient [m2 s-1] = 1.08e-6\r\n- 'Ed': Activation energy of the diffusion coefficient [eV at-1] = 0.46\r\n- 'Q_star': Heat of transport of hydrogen in zirconium [J mol-1] = 25500\r\n- 'V_star': Partial molar volume of hydrogen in the zirconium matrix [m3 mol-1] = 1.7e-6\r\n- 'Eg': Activation energy for diffusion driven growth [eV at-1] = 0.9\r\n- 'avrami_parameter': Avrami parameter for platelets [/] = 2.5\r\n- 'Eth0': 0th coefficient of formation energy polynomial [eV at-1] = 0.5655\r\n- 'Eth1': 1st coefficient of formation energy polynomial [eV at-1 K-1] = 4.0e-4\r\n- 'Eth2': 2nd coefficient of formation energy polynomial [eV at-1 K-2] = 2.0e-7\r\n- 'Eth3': 3rd coefficient of formation energy polynomial [eV at-1 K-3] = 3.0e-10\r\n- 'K_G_mob0': Pre-exponential factor for diffusion-controlled growth [s-1] = 5.53e5\r\n- 'K_G_th0': Pre-exponential factor for reaction-controlled growth [s-1] = 1.6e-5\r\n- 'K_N_0': Pre-exponential factor for nucleation kinetics [s-1] = 2.75e-5\r\n- 'K_D_0': Pre-exponential factor for dissolution kinetics [s-1] = 1110.13\r\n- 'tau': tau for mHNGD [s] = 1e4\r\n- 'g': g for mHNGD [wt.ppm] = 120\r\n- 'delta': delta for mHNGD [/] = 1.05\r\n\r\nDefault model parameters can be modified. For example, to change the default diffusion coefficient given by [Zhang et al.](https://www.nature.com/articles/srep41033) to the one given by [Kearns](https://doi.org/10.1016/0022-3115(72)90065-7), the corresponding parameters can be changed as:\r\n\r\n```python\r\nmodel_parameters['D0'] = 7.90e-7\r\nmodel_parameters['Ed'] = 0.47\r\n```\r\n\r\n### Running a simulation\r\n\r\nIn order to run a simulation, the `hngd.run` module is imported. Then, set up the input parameters described in the previous section, and use the `simulation` function as:\r\n\r\n```python\r\nimport hngd.run\r\nimport hngd.default\r\nimport numpy as np\r\n\r\nexperiment_data = (0.025, 0, 0, 1, 0)\r\n\r\nsimulation_data = ('test', 70, 2, 80, 0.01, 'mHNGD')\r\n\r\ntemperature_data = np.array([[np.nan, 0, experiment_data[0]],\r\n [ 0, 20, 20],\r\n [ 38, 400, 400],\r\n [ 48, 400, 400],\r\n [ 86, 20, 20]])\r\n\r\n\r\ninitial_hydrogen_data = np.array([[ 0, experiment_data[0]],\r\n [205, 205]])\r\n\r\nmodel_parameters = hngd.default.model_parameters\r\n\r\nhngd.run.simulation(temperature_data, initial_hydrogen_data, experiment_data, \r\n simulation_data, model_parameters)\r\n```\r\n\r\nAfter the simulation is completed, the results will be saved in a txt file which contains the time, temperature, fraction of precipitation due to growth, fraction of precipitation due to nucleation, hydrogen concentration in solid solution and hydrogen concentration in hydrides.\r\n\r\nThere are additional optional parameters for the simulation function:\r\n\r\n- `node`: Change for which node of the spatial discretization the results are saved. Defaults to 1 (node at the left of the sample). \r\n- `save_results`: If you want to save the results in a txt file. Defaults to True. \r\n- `save_last_concentration_profile`: If you want to save the concentration profile of hydrogen in solid solution and hydrogen in hydrides for the last time step. Useful to compare to some experiments in the literature. Defaults to False.\r\n- `unit_time`: Units of time in the output file, can be 's' (seconds), 'm' (minutes), 'h' (hours) or 'd' (days). Defaults to 's'.\r\n- `unit_temperature`: Units of temperature in the output file, can be 'C' (celsius) or 'K' (kelvin). Defaults to 'K'.\r\n\r\n### Running an animation\r\n\r\nIn order to run an animation, the `hngd.run` module is imported. Then, set up the input parameters described in the previous section, and use the `animation` function as:\r\n\r\n```python\r\nimport numpy as np\r\nimport hngd.default_model_parameters\r\nimport hngd.run\r\n\r\nexperiment_data = (0.025, 0, 0, 1, 0)\r\n\r\nsimulation_data = ('test', 70, 2, 40, 0.01, 'mHNGD')\r\n\r\ntemperature_data = np.array([[np.nan, 0, experiment_data[0]],\r\n [ 0, 20, 20],\r\n [ 38, 400, 400],\r\n [ 48, 400, 400],\r\n [ 86, 20, 20]])\r\n\r\ninitial_hydrogen_data = np.array([[ 0, experiment_data[0]],\r\n [205, 205]])\r\n\r\nmodel_parameters = hngd.default_model_parameters.model_parameters\r\n\r\nanimation = hngd.run.animation(temperature_data, initial_hydrogen_data, \r\n experiment_data, simulation_data, model_parameters)\r\n```\r\n\r\nThe animation shows four plots: the evolution of the hydrogen profile (top, left), the evolution of the temperature profile (top, right), the evolution of hydrogen in solid solution as a function of temperature at a single node (bottom, left), and the evolution of temperature as a function of time at a single node (bottom, right).\r\n\r\nThere are additional optional parameters for the animation function:\r\n\r\n- `node`: Which node is used to animate the temporal evolution. Defaults to the node at the middle of the sample (i. e., `simulation_data[1]//2`).\r\n- `save_animation`: If you want to save the animation as a gif. Defaults to False. *Note: When `save_animation=True`, the animation will not be displayed (to fix!).*\r\n- `interval`: Delay between frames in milliseconds. Defaults to 5.\r\n- `repeat`: Whether the animation repeats when the sequence of frames is completed. Defaults to False. *Note: Currently not working (to fix!).*\r\n\r\n### Others\r\n\r\nThere are several other possibilities of the code, such as running a time-temperature-transformation experiment (TTT diagram) using `hngd.run.TTT`, or using `hngd.run.debugger` if you are a developer and want to modify the source code and need a debugger. Some of these applications can be found in the Examples folder of this repository. \r\n\r\n## Note for Developers\r\n\r\nThis code uses the open source, just-in-time (JIT) compiler from the [numba](https://numba.pydata.org/) library, which translates Python functions to optimized machine code at runtime using the industry-standard LLVM compiler library.\r\n\r\nIf you are making changes to the code and want to use the debugger to do some testing, you will have to disable numba. This can be done by setting:\r\n\r\n```\r\n DISABLE_JIT: True\r\n```\r\n\r\nin the `.numba_config.yaml` file which is located at the `hngd` folder.\r\n\r\n## References\r\n\r\nSome references for the HNGD model:\r\n \r\n[1] Lacroix E., *Modeling zirconium hydride precipitation and dissolution in zirconium alloys*, PhD Thesis, The Pennsylvania State University (2019).\r\n\r\n[2] Passelaigue F., *Hydride Nucleation-Growth-Dissolution model: Implementation in BISON*, MSc. Thesis, The Pennsylvania State University (2020).\r\n\r\n[3] Passelaigue F., Lacroix E., Pastore G. and Motta A. T., *Implementation and validation of the Hydride Nucleation-Growth-Dissolution (HNGD) model in BISON*, Journal of Nuclear Materials 544, pp. 152683 (2021). [https://doi.org/10.1016/j.jnucmat.2020.152683](https://doi.org/10.1016/j.jnucmat.2020.152683).\r\n\r\n[4] Passelaigue F., Simon, P. A. and Motta, A. T., *Predicting the hydride rim by improving the solubility limits in the Hydride Nucleation-Growth-Dissolution (HNGD) model*, Journal of Nuclear Materials 558, pp. 153363 (2022). [https://doi.org/10.1016/j.jnucmat.2021.153363](https://doi.org/10.1016/j.jnucmat.2021.153363).\r\n\r\n[5] Bin Seo S., Duchnowski E. M., Motta A. T., Kammenzind B. F. and Brown N. R.,*Sensitivity analysis for characterizing the impact of HNGD model on the prediction of hydrogen redistribution in Zircaloy cladding using BISON code*, Nuclear Engineering and Design 393, pp. 111813 (2022). [https://doi.org/10.1016/j.nucengdes.2022.111813](https://doi.org/10.1016/j.nucengdes.2022.111813).\r\n\r\n[6] Lee C. and Lee, Y., *Simulation of hydrogen diffusion along the axial direction in zirconium cladding tube during dry storage*, Journal of Nuclear Materials 579, pp. 154352 (2023). [https://doi.org/10.1016/j.jnucmat.2023.154352](https://doi.org/10.1016/j.jnucmat.2023.154352)\r\n",
"bugtrack_url": null,
"license": "BSD-3-Clause",
"summary": "Implementation of the Hydride Nucleation-Growth-Dissolution (HNGD) model. Simulates hydrogen behaviour in a 1D geometry using an explicit finite difference scheme (Euler method).",
"version": "1.0.1",
"project_urls": {
"Repository": "https://github.com/franciscorotea/"
},
"split_keywords": [
"hngd",
"hydrogen",
"hydrides",
"nuclear fuel cladding",
"diffusion"
],
"urls": [
{
"comment_text": "",
"digests": {
"blake2b_256": "3e45afe2f7046180a0e779342daff5a5fb556c64d963ddc22a85fd8fd9c1ea67",
"md5": "577827d2752954224f3c55929edf3eb1",
"sha256": "0a58312f7c5ddbf82eca443121d32d8432b0ea1c8ec3798101d341cbd4073873"
},
"downloads": -1,
"filename": "hngd-1.0.1-py3-none-any.whl",
"has_sig": false,
"md5_digest": "577827d2752954224f3c55929edf3eb1",
"packagetype": "bdist_wheel",
"python_version": "py3",
"requires_python": ">=3.10",
"size": 25487,
"upload_time": "2023-09-18T19:55:36",
"upload_time_iso_8601": "2023-09-18T19:55:36.973806Z",
"url": "https://files.pythonhosted.org/packages/3e/45/afe2f7046180a0e779342daff5a5fb556c64d963ddc22a85fd8fd9c1ea67/hngd-1.0.1-py3-none-any.whl",
"yanked": false,
"yanked_reason": null
},
{
"comment_text": "",
"digests": {
"blake2b_256": "4c48f0efbd53c126771d3fc1fd11ac277b995ca90b965fc5c0d1edf24545fe76",
"md5": "b845ee27bc668acb3bf529338f3497b8",
"sha256": "c45126e1fd9df76100c96473589f5a1d42d01a988dd422db9b7e319ee8cdabb7"
},
"downloads": -1,
"filename": "hngd-1.0.1.tar.gz",
"has_sig": false,
"md5_digest": "b845ee27bc668acb3bf529338f3497b8",
"packagetype": "sdist",
"python_version": "source",
"requires_python": ">=3.10",
"size": 11939710,
"upload_time": "2023-09-18T19:55:40",
"upload_time_iso_8601": "2023-09-18T19:55:40.397365Z",
"url": "https://files.pythonhosted.org/packages/4c/48/f0efbd53c126771d3fc1fd11ac277b995ca90b965fc5c0d1edf24545fe76/hngd-1.0.1.tar.gz",
"yanked": false,
"yanked_reason": null
}
],
"upload_time": "2023-09-18 19:55:40",
"github": false,
"gitlab": false,
"bitbucket": false,
"codeberg": false,
"lcname": "hngd"
}