| Name | muller-eot JSON |
| Version |
1.4.3
 JSON
JSON |
| download |
| home_page | None |
| Summary | A Python package for M. Müller implementation of the 'Equation of Time - Problem in Astronomy' to calculate EOT and the effect of eccentricity/obliquity |
| upload_time | 2024-08-14 05:47:02 |
| maintainer | None |
| docs_url | None |
| author | None |
| requires_python | >3.9 |
| license | MIT License Copyright (c) 2022 C. Y. Schneck Permission is hereby granted, free of charge, to any person obtaining a copy of this software and associated documentation files (the "Software"), to deal in the Software without restriction, including without limitation the rights to use, copy, modify, merge, publish, distribute, sublicense, and/or sell copies of the Software, and to permit persons to whom the Software is furnished to do so, subject to the following conditions: The above copyright notice and this permission notice shall be included in all copies or substantial portions of the Software. THE SOFTWARE IS PROVIDED "AS IS", WITHOUT WARRANTY OF ANY KIND, EXPRESS OR IMPLIED, INCLUDING BUT NOT LIMITED TO THE WARRANTIES OF MERCHANTABILITY, FITNESS FOR A PARTICULAR PURPOSE AND NONINFRINGEMENT. IN NO EVENT SHALL THE AUTHORS OR COPYRIGHT HOLDERS BE LIABLE FOR ANY CLAIM, DAMAGES OR OTHER LIABILITY, WHETHER IN AN ACTION OF CONTRACT, TORT OR OTHERWISE, ARISING FROM, OUT OF OR IN CONNECTION WITH THE SOFTWARE OR THE USE OR OTHER DEALINGS IN THE SOFTWARE. |
| keywords |
astronomy
python
eot
equation of time
eccentricity
obliquity
orbital dynamics
|
| VCS |
 |
| bugtrack_url |
|
| requirements |
No requirements were recorded.
|
| Travis-CI |
No Travis.
|
| coveralls test coverage |
No coveralls.
|
# Muller-EOT



A Python package for [M. Müller implementation of the "Equation of Time - Problem in Astronomy"](http://info.ifpan.edu.pl/firststep/aw-works/fsII/mul/mueller.pdf) to calculate the Equation of Time based on the individual effect of eccentricity and obliquity
## Quickstart: muller-eot
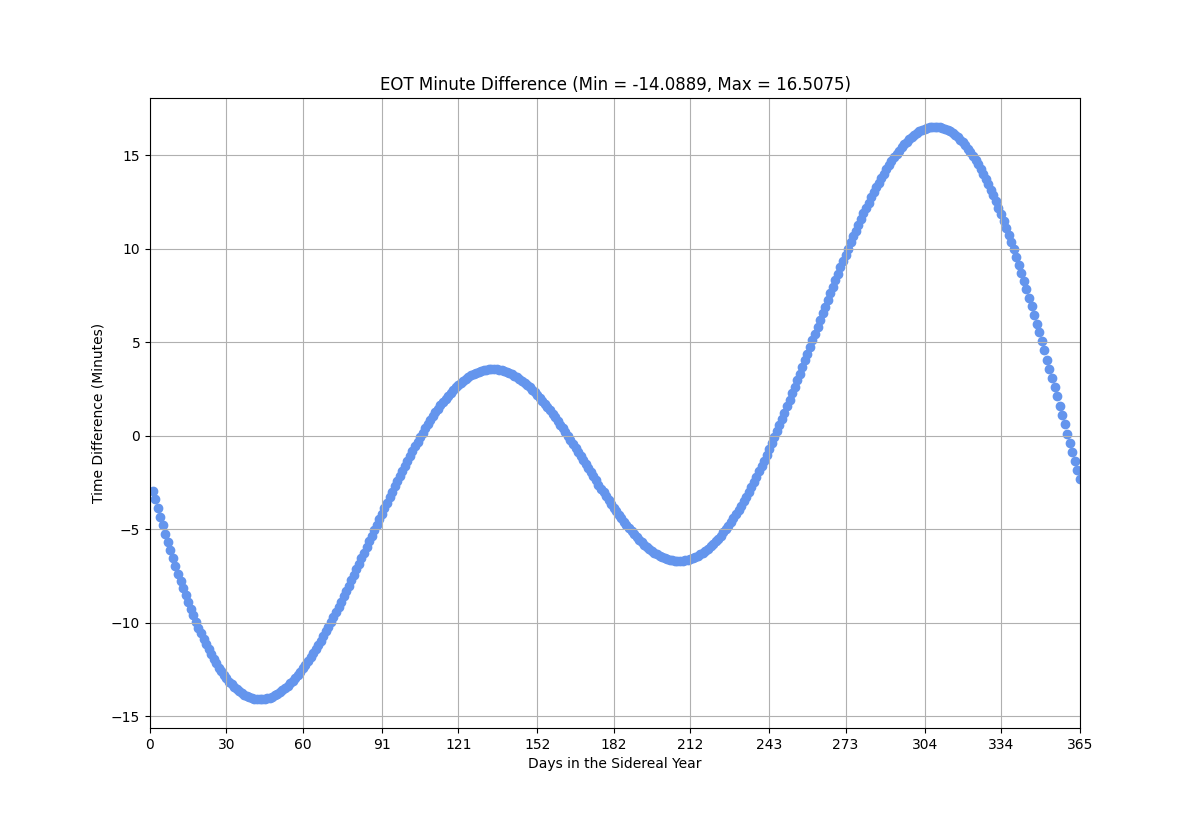
Get a list of differences in time for each day of the Earth's orbit and then plot it as a function of days in orbit
```
import muller_eot
earth_eot = muller_eot.EOT(eccentricity=0.0167, obliquity=23.45, orbit_period=365.25)
earth_eot.plotEOT()
```
## Install
PyPi pip install at [pypi.org/project/muller-eot/](https://pypi.org/project/muller-eot/)
```
pip install muller-eot
```
## Functions
The combined effect of eccentricity and obliquity create the Equation of Time components.
| Effect of Eccentricity | Effect of Obliquity |
| ------------- | ------------- |
| 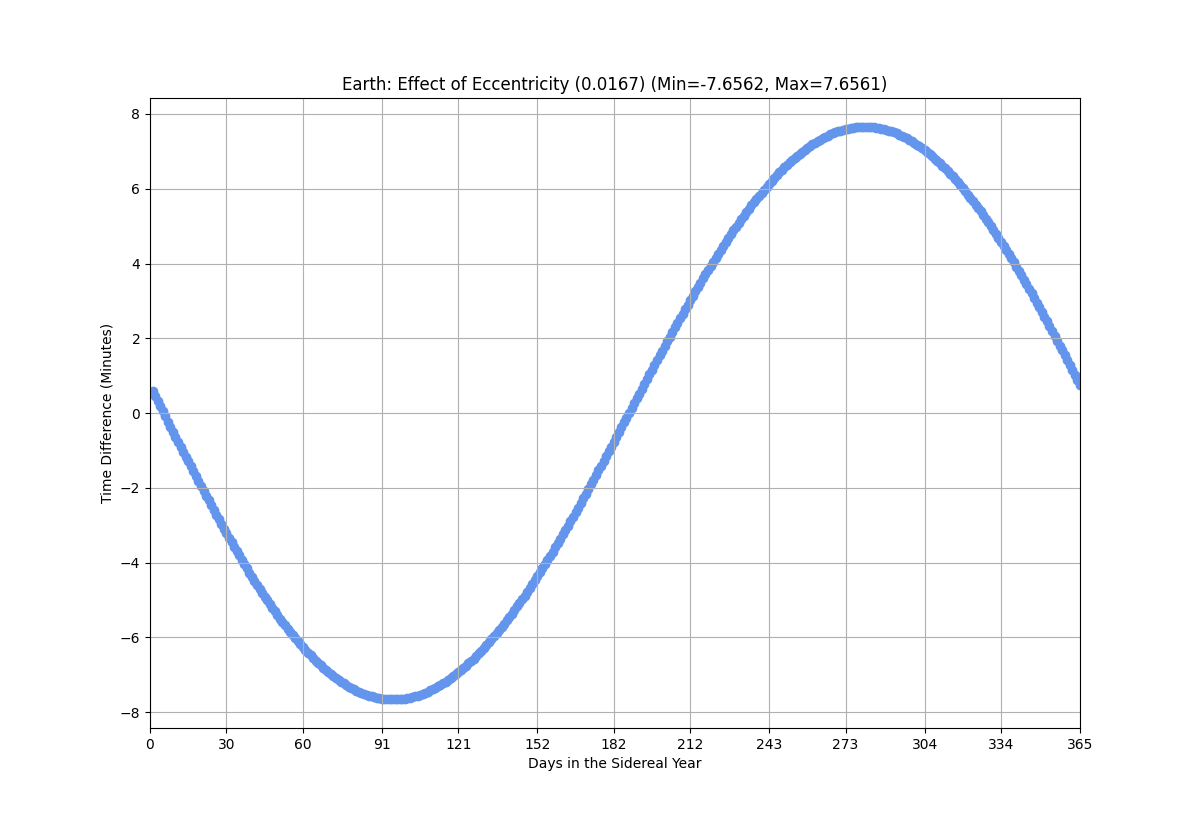 | 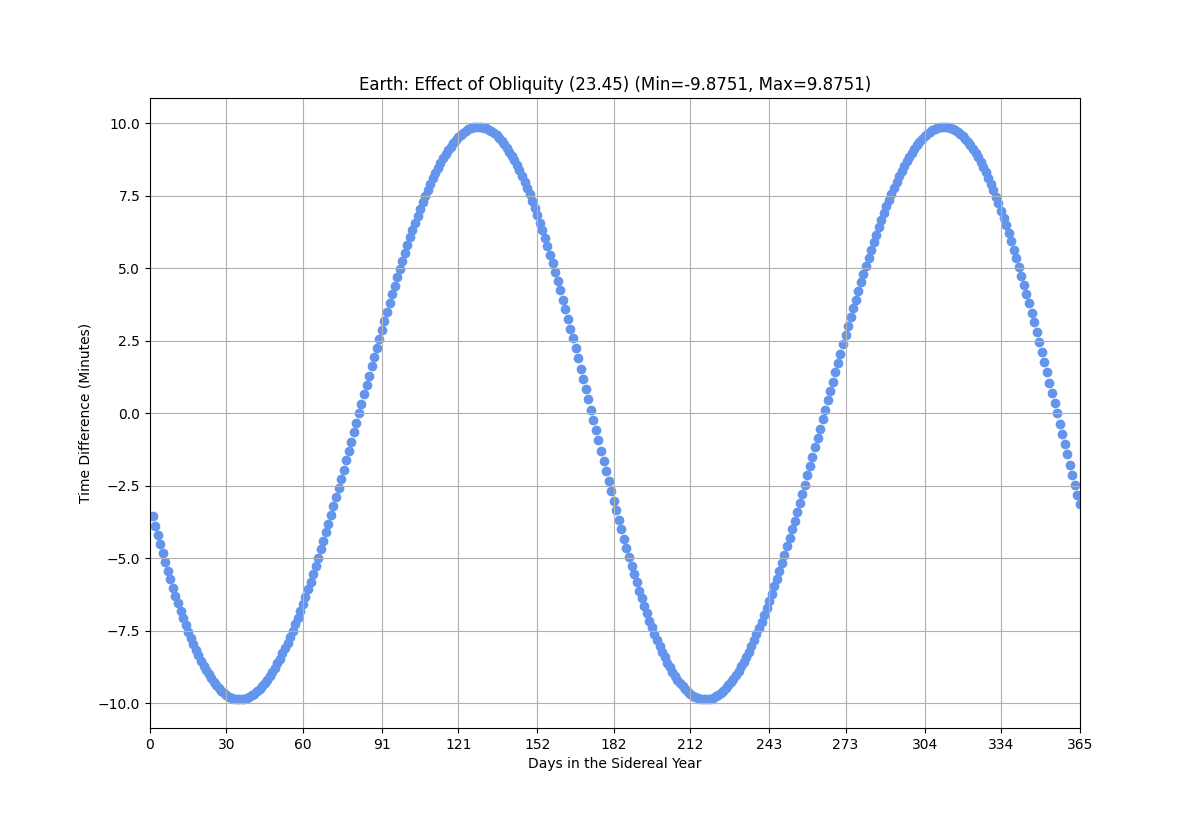 |
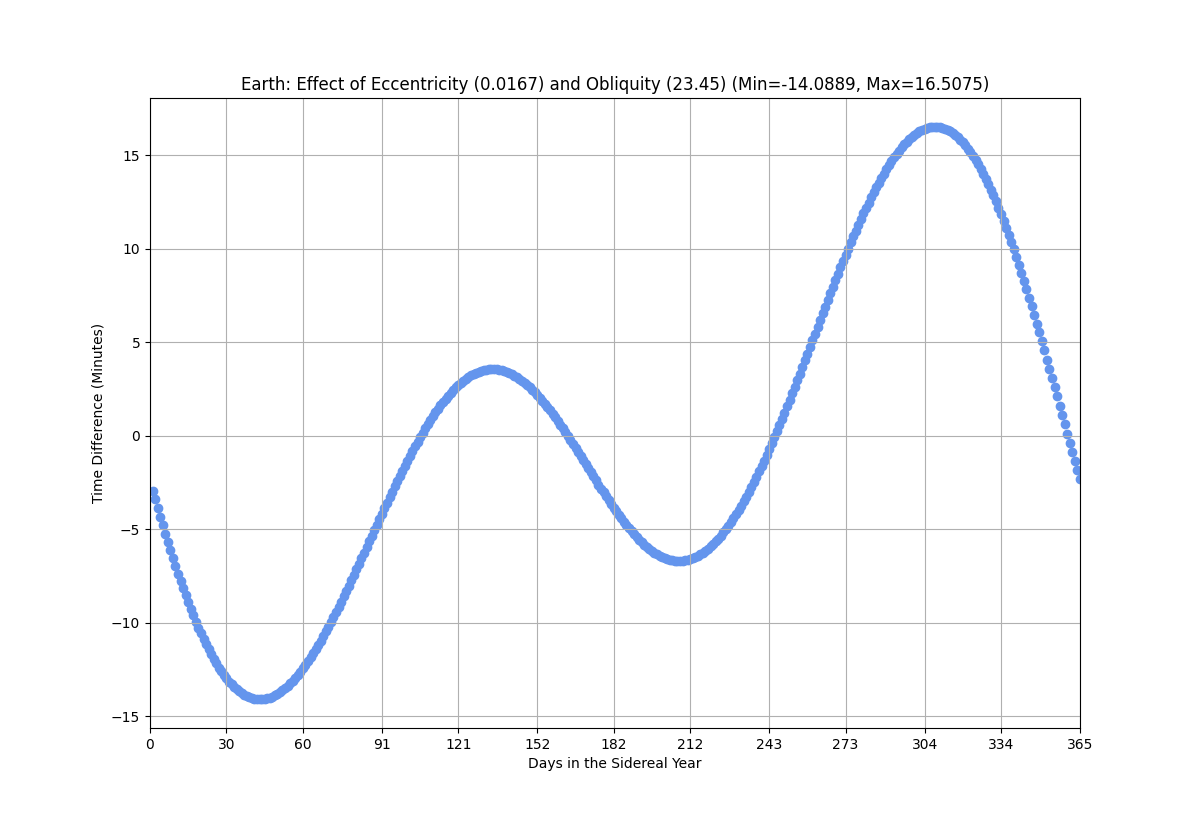
Combined Effect of the Eccentricity and Obliquity = Equation of Time
### EOT Object
All Equation of Time calculations are done as a part of the EOT class object. First, create an EOT object for a specific eccentricity, obliquity, and orbit period (in days)
```python
import muller_eot
muller_eot.EOT(eccentricity=None,
obliquity=None,
orbit_period=None)
```
- **[REQUIRED]** eccentricity (float/int): eccentricity of the planet's orbit
- **[REQUIRED]** obliquity (float/int): obliquity/axial tilt of the planet
- **[REQUIRED]** orbit_period (float/int): days in a solar year
### EOT Class Attributes and Functions
**eotDayAndMinutes**
Returns a dictionary for the difference in time for each day in a year {number_day: time difference}
```python
EOT.eotDayAndMinutes
```
**plotEOT**
Plot the differences in time for the EOT as well as the individual effect of obliquity and eccentricity
```python
EOT.plotEOT(plot_title=None,
plot_x_title=None,
plot_y_title=None,
show_plot=True,
fig_plot_color="cornflowerblue",
figsize_n=12,
figsize_dpi=100,
save_plot_name=None)
```
- *[OPTIONAL]* plot_title (string): Title of plot, defaults to `EOT Minute Difference (Min = <negative minutes>, Max = <postive minutes>)`
- *[OPTIONAL]* plot_x_title (string): X-axis title, defaults to `Days in the Sidereal Year`
- *[OPTIONAL]* plot_y_title (string): Y-axis title, defaults to `Time Difference (Minutes)`
- *[OPTIONAL]* show_plot (boolean): Show plot (triggers plt.show()), useful when generating multiple plots at once in the background, defaults to True
- *[OPTIONAL]* fig_plot_color (string): Scatter plot color, defaults to `cornflowerblue` blue
- *[OPTIONAL]* figsize_n (int/float): Figure size nxn, defaults to 12x12
- *[OPTIONAL]* figsize_dpi (int/lfoat): Figure DPI, defaults to 100
- *[OPTIONAL]* save_plot_name (boolean): Save plot as output, defaults to None (does not save)
## Background
The length of a day on Earth is only close to being 24 hours four times a year. For the rest of the year when the sun is at its highest point (solar noon), a clock can run as much as 16 minutes ahead (12:16pm) or 13 minutes behind (11:47am). This discrepancy is the result of the combined effect of a planet's obliquity (axial tilt) and its eccentricity (as well as other smaller gravitational forces like moons that are ignored here). Both of these features form two sine curves that oscillate throughout the year. The combined sum
of these two curves form the Equation of Time, a non-uniform change in time to fix to a clock.
A planet with an obliquity of 0° and perfectly circular orbit (zero eccentricity) would have
no difference in the Expected Solar Noon and the Actual Solar Noon.
To calculate the difference in time for an individual day:
<p align="center">
<img src="https://user-images.githubusercontent.com/22159116/203877814-c2d710f3-0681-4f72-8607-0f96e2a33256.png" />
</p>
Equation of Time = (Apparent Solar Time) - (Mean Solar Time)
**Effect of Eccentricity:**
<p align="center">
<img src="https://user-images.githubusercontent.com/22159116/203484492-bf0f6098-fe13-44d3-b372-bcb8cc4120f8.png" />
</p>
**Effect of Obliquity:**
<p align="center">
<img src="https://user-images.githubusercontent.com/22159116/203484389-613ffb3e-9719-4962-a316-eeeb887af1c5.png" />
</p>
"Equation of time is determined by the following parameters: the eccentricity of
the orbit of the Earth, the angle between the ecliptic and the equatorial planes, the
angle P between the winter solstice and the perihelion relative to the sun or:
the time span ∆t from the beginning of winter to the passage through periehlion" (Müller, 1995)
<p align="center">
<img src="https://user-images.githubusercontent.com/22159116/203484797-23c81e99-0eee-4431-bc21-31429a615e4f.png" />
</p>
<p align="center">
<img src="https://user-images.githubusercontent.com/22159116/203484692-b07bad99-3c6c-43e5-904f-04200f72c571.png" />
</p>
The effect of eccentricity is the result of Kepler's Law where:
"Two well-known features of our solar system are at the basis of the variations
in the apparent motion of the sun: 1.) According to Kepler's second law, the angular
velocity of the Earth relative to the sun varies throughout a year. 2) Equal angles
which the sun in its apparent movement goes through in the eclipitic do not correspond
to equal angles we measure on the equatorial plane. However, it is these latter angles
which are relevant for the measure of time, since the daily movement of the sun is
parallel to the equatorial plane" (Müller, 1995)
**Effect on Angular Velocity (on Eccentricity):**
As a result of Kepler's law, planets moving in an ellipitc orbit will have variable angular velocity
as a result of the second law where the area swept during a constant period of time is constant (=dA/dt)
<p align="center">
<img src="https://user-images.githubusercontent.com/22159116/203687968-4055d194-afe0-49e8-8b73-94f1b58a3969.png" />
</p>
"1.) parameter: the eccentricity. If e = 0 a regular variation results that is caused by
the inclination of the ecliptic plane. The deviations of the apparent solar time from the
mean solar time increase with growing e in winter and autumn. Thus, the yearly variation
becomes dominant. Since at the perihelion and aphelion the equation of time is only a
function of the ecliptic inclination and the angle P, all plots have the same value at these
two points.
2.) parameter: the inclination of the ecliptic. ε = 0 yields a plot which is symmetric to
the passage through the aphelion. The greater ε the more dominant the variation with a
period of half a year. All plots have four common points at the beginning of each season,
for the equation of time depends only on the two other parameters there (eccentricity
and P). As the projection from the ecliptic plane onto the equatorial plane does not
change the polar angle relative to the winter solstice, ε does not influence the value of the
equation of time at the beginning of a season.
3.) parameter: the time interval between the beginning of winter and the passage
through the perihelion. If ∆t = 0 the two main variations vanish both at the beginning
of winter and summer (because winter begins when the earth passes the perihelion; the
aphelion is the summer solstice). Therefore, the resulting function is symmetric and the
extreme values are in autumn and winter. If ∆t increases, the two components tend to
compensate each other in winter whereas the negative value in summer begins to dominate." (Müller, 1995)
Equation of Time is the combination of the effect of eccentricity and obliquity
<p align="center">
<img src="https://user-images.githubusercontent.com/22159116/203484851-c96be35a-2d4a-44df-a2ee-a9d88974aa9e.png" />
</p>
### TODO:
- Pytests
- calculateOrbitalPeriod(semimajor_axis)
- calculateDistanceBetweenSolisticePerhelion()
- calculatePerihelionDay()
- calculateWinterSolsticeDay()
- calculateEccentricity()
## Development Environment
To run or test against `muller_eot` github repo/fork, a development environment can be created via conda/miniconda
First, [install Miniconda](https://docs.conda.io/projects/miniconda/en/latest/miniconda-install.html)
Then, using the existing `environment.yml`, a new conda environment can be create to run/test scripts against
```
conda env create --file environment.yml
```
Once the environment has been built, activate the environment:
```
conda activate muller_eot
```
Raw data
{
"_id": null,
"home_page": null,
"name": "muller-eot",
"maintainer": null,
"docs_url": null,
"requires_python": ">3.9",
"maintainer_email": null,
"keywords": "astronomy, python, eot, equation of time, eccentricity, obliquity, orbital dynamics",
"author": null,
"author_email": "Cora Schneck <cyschneck@gmail.com>",
"download_url": "https://files.pythonhosted.org/packages/d2/88/d052a4f7fd6acbe3bf45595d3b779886d045db0187505f5ad4ce6163c96c/muller_eot-1.4.3.tar.gz",
"platform": null,
"description": "# Muller-EOT\n\n\n\n\nA Python package for [M. M\u00fcller implementation of the \"Equation of Time - Problem in Astronomy\"](http://info.ifpan.edu.pl/firststep/aw-works/fsII/mul/mueller.pdf) to calculate the Equation of Time based on the individual effect of eccentricity and obliquity\n\n## Quickstart: muller-eot\n\nGet a list of differences in time for each day of the Earth's orbit and then plot it as a function of days in orbit\n\n```\nimport muller_eot\n\nearth_eot = muller_eot.EOT(eccentricity=0.0167, obliquity=23.45, orbit_period=365.25)\nearth_eot.plotEOT()\n```\n\n\n## Install\nPyPi pip install at [pypi.org/project/muller-eot/](https://pypi.org/project/muller-eot/)\n\n```\npip install muller-eot\n```\n\n## Functions\nThe combined effect of eccentricity and obliquity create the Equation of Time components.\n\n| Effect of Eccentricity | Effect of Obliquity |\n| ------------- | ------------- |\n|  |  |\n\nCombined Effect of the Eccentricity and Obliquity = Equation of Time\n\n\n### EOT Object\nAll Equation of Time calculations are done as a part of the EOT class object. First, create an EOT object for a specific eccentricity, obliquity, and orbit period (in days)\n```python\nimport muller_eot\nmuller_eot.EOT(eccentricity=None,\n\t\tobliquity=None,\n\t\torbit_period=None)\n```\n- **[REQUIRED]** eccentricity (float/int): eccentricity of the planet's orbit\n- **[REQUIRED]** obliquity (float/int): obliquity/axial tilt of the planet\n- **[REQUIRED]** orbit_period (float/int): days in a solar year\n\n\n### EOT Class Attributes and Functions\n\n**eotDayAndMinutes**\nReturns a dictionary for the difference in time for each day in a year {number_day: time difference}\n```python\nEOT.eotDayAndMinutes\n```\n\n**plotEOT**\nPlot the differences in time for the EOT as well as the individual effect of obliquity and eccentricity\n```python\nEOT.plotEOT(plot_title=None,\n\t\tplot_x_title=None,\n\t\tplot_y_title=None,\n\t\tshow_plot=True,\n\t\tfig_plot_color=\"cornflowerblue\",\n\t\tfigsize_n=12,\n\t\tfigsize_dpi=100,\n\t\tsave_plot_name=None)\n```\n- *[OPTIONAL]* plot_title (string): Title of plot, defaults to `EOT Minute Difference (Min = <negative minutes>, Max = <postive minutes>)`\n- *[OPTIONAL]* plot_x_title (string): X-axis title, defaults to `Days in the Sidereal Year`\n- *[OPTIONAL]* plot_y_title (string): Y-axis title, defaults to `Time Difference (Minutes)`\n- *[OPTIONAL]* show_plot (boolean): Show plot (triggers plt.show()), useful when generating multiple plots at once in the background, defaults to True\n- *[OPTIONAL]* fig_plot_color (string): Scatter plot color, defaults to `cornflowerblue` blue\n- *[OPTIONAL]* figsize_n (int/float): Figure size nxn, defaults to 12x12\n- *[OPTIONAL]* figsize_dpi (int/lfoat): Figure DPI, defaults to 100\n- *[OPTIONAL]* save_plot_name (boolean): Save plot as output, defaults to None (does not save)\n\n## Background\n\nThe length of a day on Earth is only close to being 24 hours four times a year. For the rest of the year when the sun is at its highest point (solar noon), a clock can run as much as 16 minutes ahead (12:16pm) or 13 minutes behind (11:47am). This discrepancy is the result of the combined effect of a planet's obliquity (axial tilt) and its eccentricity (as well as other smaller gravitational forces like moons that are ignored here). Both of these features form two sine curves that oscillate throughout the year. The combined sum\nof these two curves form the Equation of Time, a non-uniform change in time to fix to a clock.\nA planet with an obliquity of 0\u00b0 and perfectly circular orbit (zero eccentricity) would have\nno difference in the Expected Solar Noon and the Actual Solar Noon.\n\nTo calculate the difference in time for an individual day:\n<p align=\"center\">\n <img src=\"https://user-images.githubusercontent.com/22159116/203877814-c2d710f3-0681-4f72-8607-0f96e2a33256.png\" />\n</p>\n\nEquation of Time = (Apparent Solar Time) - (Mean Solar Time) \n\n**Effect of Eccentricity:**\n<p align=\"center\">\n <img src=\"https://user-images.githubusercontent.com/22159116/203484492-bf0f6098-fe13-44d3-b372-bcb8cc4120f8.png\" />\n</p>\n\n**Effect of Obliquity:**\n<p align=\"center\">\n <img src=\"https://user-images.githubusercontent.com/22159116/203484389-613ffb3e-9719-4962-a316-eeeb887af1c5.png\" />\n</p>\n\n\"Equation of time is determined by the following parameters: the eccentricity of \nthe orbit of the Earth, the angle between the ecliptic and the equatorial planes, the \nangle P between the winter solstice and the perihelion relative to the sun or: \nthe time span \u2206t from the beginning of winter to the passage through periehlion\" (M\u00fcller, 1995)\n\n<p align=\"center\">\n <img src=\"https://user-images.githubusercontent.com/22159116/203484797-23c81e99-0eee-4431-bc21-31429a615e4f.png\" />\n</p>\n<p align=\"center\">\n <img src=\"https://user-images.githubusercontent.com/22159116/203484692-b07bad99-3c6c-43e5-904f-04200f72c571.png\" />\n</p>\n\nThe effect of eccentricity is the result of Kepler's Law where:\n\n\"Two well-known features of our solar system are at the basis of the variations\n in the apparent motion of the sun: 1.) According to Kepler's second law, the angular\n velocity of the Earth relative to the sun varies throughout a year. 2) Equal angles\n which the sun in its apparent movement goes through in the eclipitic do not correspond\n to equal angles we measure on the equatorial plane. However, it is these latter angles\n which are relevant for the measure of time, since the daily movement of the sun is\n parallel to the equatorial plane\" (M\u00fcller, 1995)\n \n**Effect on Angular Velocity (on Eccentricity):**\n\nAs a result of Kepler's law, planets moving in an ellipitc orbit will have variable angular velocity \nas a result of the second law where the area swept during a constant period of time is constant (=dA/dt)\n\n<p align=\"center\">\n <img src=\"https://user-images.githubusercontent.com/22159116/203687968-4055d194-afe0-49e8-8b73-94f1b58a3969.png\" />\n</p>\n\n\"1.) parameter: the eccentricity. If e = 0 a regular variation results that is caused by\nthe inclination of the ecliptic plane. The deviations of the apparent solar time from the\nmean solar time increase with growing e in winter and autumn. Thus, the yearly variation\nbecomes dominant. Since at the perihelion and aphelion the equation of time is only a\nfunction of the ecliptic inclination and the angle P, all plots have the same value at these\ntwo points.\n2.) parameter: the inclination of the ecliptic. \u03b5 = 0 yields a plot which is symmetric to\nthe passage through the aphelion. The greater \u03b5 the more dominant the variation with a\nperiod of half a year. All plots have four common points at the beginning of each season,\nfor the equation of time depends only on the two other parameters there (eccentricity\nand P). As the projection from the ecliptic plane onto the equatorial plane does not\nchange the polar angle relative to the winter solstice, \u03b5 does not influence the value of the\nequation of time at the beginning of a season.\n3.) parameter: the time interval between the beginning of winter and the passage\nthrough the perihelion. If \u2206t = 0 the two main variations vanish both at the beginning\nof winter and summer (because winter begins when the earth passes the perihelion; the\naphelion is the summer solstice). Therefore, the resulting function is symmetric and the\nextreme values are in autumn and winter. If \u2206t increases, the two components tend to\ncompensate each other in winter whereas the negative value in summer begins to dominate.\" (M\u00fcller, 1995)\n\nEquation of Time is the combination of the effect of eccentricity and obliquity\n<p align=\"center\">\n <img src=\"https://user-images.githubusercontent.com/22159116/203484851-c96be35a-2d4a-44df-a2ee-a9d88974aa9e.png\" />\n</p>\n\n### TODO:\n- Pytests\n- calculateOrbitalPeriod(semimajor_axis)\n- calculateDistanceBetweenSolisticePerhelion()\n- calculatePerihelionDay()\n- calculateWinterSolsticeDay()\n- calculateEccentricity()\n\n## Development Environment\n\nTo run or test against `muller_eot` github repo/fork, a development environment can be created via conda/miniconda\n\nFirst, [install Miniconda](https://docs.conda.io/projects/miniconda/en/latest/miniconda-install.html)\n\nThen, using the existing `environment.yml`, a new conda environment can be create to run/test scripts against\n\n```\nconda env create --file environment.yml\n```\nOnce the environment has been built, activate the environment:\n```\nconda activate muller_eot\n```\n",
"bugtrack_url": null,
"license": "MIT License Copyright (c) 2022 C. Y. Schneck Permission is hereby granted, free of charge, to any person obtaining a copy of this software and associated documentation files (the \"Software\"), to deal in the Software without restriction, including without limitation the rights to use, copy, modify, merge, publish, distribute, sublicense, and/or sell copies of the Software, and to permit persons to whom the Software is furnished to do so, subject to the following conditions: The above copyright notice and this permission notice shall be included in all copies or substantial portions of the Software. THE SOFTWARE IS PROVIDED \"AS IS\", WITHOUT WARRANTY OF ANY KIND, EXPRESS OR IMPLIED, INCLUDING BUT NOT LIMITED TO THE WARRANTIES OF MERCHANTABILITY, FITNESS FOR A PARTICULAR PURPOSE AND NONINFRINGEMENT. IN NO EVENT SHALL THE AUTHORS OR COPYRIGHT HOLDERS BE LIABLE FOR ANY CLAIM, DAMAGES OR OTHER LIABILITY, WHETHER IN AN ACTION OF CONTRACT, TORT OR OTHERWISE, ARISING FROM, OUT OF OR IN CONNECTION WITH THE SOFTWARE OR THE USE OR OTHER DEALINGS IN THE SOFTWARE. ",
"summary": "A Python package for M. M\u00fcller implementation of the 'Equation of Time - Problem in Astronomy' to calculate EOT and the effect of eccentricity/obliquity",
"version": "1.4.3",
"project_urls": {
"Issues": "https://github.com/cyschneck/Muller-EOT/issues",
"Repository": "https://github.com/cyschneck/Muller-EOT"
},
"split_keywords": [
"astronomy",
" python",
" eot",
" equation of time",
" eccentricity",
" obliquity",
" orbital dynamics"
],
"urls": [
{
"comment_text": "",
"digests": {
"blake2b_256": "ff09b8ce4d301a24a6ecfcd0a243fd77d449cec274031edc9da98a5b30f2012d",
"md5": "aa52a5a36e8bde8119e17e38a9ac9602",
"sha256": "4e1d5ea5169bca9dd12e083aecd2e076f84a1eb43b7a1cfdd610749ac3f4557d"
},
"downloads": -1,
"filename": "muller_eot-1.4.3-py3-none-any.whl",
"has_sig": false,
"md5_digest": "aa52a5a36e8bde8119e17e38a9ac9602",
"packagetype": "bdist_wheel",
"python_version": "py3",
"requires_python": ">3.9",
"size": 11211,
"upload_time": "2024-08-14T05:47:01",
"upload_time_iso_8601": "2024-08-14T05:47:01.157376Z",
"url": "https://files.pythonhosted.org/packages/ff/09/b8ce4d301a24a6ecfcd0a243fd77d449cec274031edc9da98a5b30f2012d/muller_eot-1.4.3-py3-none-any.whl",
"yanked": false,
"yanked_reason": null
},
{
"comment_text": "",
"digests": {
"blake2b_256": "d288d052a4f7fd6acbe3bf45595d3b779886d045db0187505f5ad4ce6163c96c",
"md5": "13c916e0f89ab312bc4c20ab658f2c1c",
"sha256": "e31287a12dff6ac340700a5397c332399181591cb3c3f5204544a25a732923c9"
},
"downloads": -1,
"filename": "muller_eot-1.4.3.tar.gz",
"has_sig": false,
"md5_digest": "13c916e0f89ab312bc4c20ab658f2c1c",
"packagetype": "sdist",
"python_version": "source",
"requires_python": ">3.9",
"size": 13659,
"upload_time": "2024-08-14T05:47:02",
"upload_time_iso_8601": "2024-08-14T05:47:02.592850Z",
"url": "https://files.pythonhosted.org/packages/d2/88/d052a4f7fd6acbe3bf45595d3b779886d045db0187505f5ad4ce6163c96c/muller_eot-1.4.3.tar.gz",
"yanked": false,
"yanked_reason": null
}
],
"upload_time": "2024-08-14 05:47:02",
"github": true,
"gitlab": false,
"bitbucket": false,
"codeberg": false,
"github_user": "cyschneck",
"github_project": "Muller-EOT",
"travis_ci": false,
"coveralls": false,
"github_actions": false,
"requirements": [],
"lcname": "muller-eot"
}
