# nonlincausality
Python package for Granger causality test with nonlinear forecasting methods (neural networks).
This package contains two types of functions.
As a traditional Granger causality test is using linear regression for prediction it may not capture more complex causality relations.
The first type of presented functions are using nonlinear forecasting methods (neural networks) for prediction instead of linear regression.
For each tested lag this function is creating 2 models. The first one is forecasting the present value of X based on n=current lag past values of X,
while the second model is forecasting the same value based on n=current lag past values of X and Y time series.
If the prediction error of the second model is statistically significantly smaller than the error of the first model then it means that Y is G-causing X (Y➔X).
It is also possible to test conditional causality using those functions.
The functions based on neural networks can test the causality on the given test set (which is recomended). The first type of function contains: `nonlincausalityMLP()`, `nonlincausalityLSTM()`, `nonlincausalityGRU()`, `nonlincausalityNN()` (and additionally `nonlincausalityARIMA()`, as there is no other Python implementation of ARIMA/ARIMAX models for causality analysis).
The second type of functions is for measuring the change of causality over time.
Those functions are using first type functions to create the forecasting models.
They calculate the measure of the causality in a given time window (`w1`) with a given step (`w2`).
The measure of change of the causality over time is expressed by the equation:
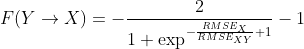
Those functions can operate with multiple time series and test causal relations for each pair of signals.
The second type of function contains: `nonlincausalitymeasureMLP()`, `nonlincausalitymeasureLSTM()`, `nonlincausalitymeasureGRU()`, `nonlincausalitymeasureNN()` and `nonlincausalitymeasureARIMA()`.
## Author
**Maciej Rosoł**
mrosol5@gmail.com, maciej.rosol.dokt@pw.edu.pl <br />
Warsaw University of Technology
## Reference
Maciej Rosoł, Marcel Młyńczak, Gerard Cybulski <br />
Granger causality test with nonlinear neural-network-based methods: Python package and simulation study. <br />
Computer Methods and Programs in Biomedicine, Volume 216, 2022 <br />
https://doi.org/10.1016/j.cmpb.2022.106669
## Example usage
Assume that there are two signals X and Y, which are stored in the variable `data`, where X is in the first column and Y in the second. The variable `data` was split into `data_train` (first 70% of the data) and `data_test` (last 30% of the data). Then to test the presence of causality Y➔X for the given lag values (defined as a list e.g. `[50, 150]`) the following functions can be used (all arguments are examples and may vary depending on the data.).
### MLP
```
results = nonlincausalityMLP(x=data_train, maxlag=lags, Dense_layers=2, Dense_neurons=[100, 100], x_test=data_test, run=1, add_Dropout=True, Dropout_rate=0.01, epochs_num=[50, 100], learning_rate=[0.001, 0.0001], batch_size_num=128, verbose=True, plot=True)
```
### GRU
```
results_GRU = nonlincausalityGRU(x=data_train, maxlag=lags, GRU_layers=2, GRU_neurons=[25, 25], Dense_layers=2, Dense_neurons=[100, 100], x_test=data_test, run=3, add_Dropout=True, Dropout_rate=0.01, epochs_num=[50, 100], learning_rate=[0.001, 0.0001], batch_size_num=128, verbose=False, plot=True)
```
### LSTM
```
results_LSTM = nonlincausalityLSTM(x=data_train, maxlag=lags, LSTM_layers=2, LSTM_neurons=[25, 25], Dense_layers=2, Dense_neurons=[100, 100], x_test=data_test, run=3, add_Dropout=True, Dropout_rate=0.01, epochs_num=[50, 100], learning_rate=[0.001, 0.0001], batch_size_num=128, verbose=False, plot=True)
```
### NN
```
results_NN = nonlincausalityNN(x=data_train, maxlag=lags, NN_config=["l", "dr", "g", "dr", "d", "dr"], NN_neurons=[5, 0.1, 5, 0.1, 5, 0.1], x_test=data_test, run=3, epochs_num=[50, 100], learning_rate=[0.001, 0.0001], batch_size_num=128, verbose=False, plot=True)
```
### ARIMA
```
results_ARIMA = nonlincausalityARIMA(x=data_train, maxlag=lags, x_test=data_train)
```
### Change of causality over time
For a deeper understanding of the dependency between the signals, the change of causality over time might be studied using the above-mentioned functions. The example usage for MLP neural networks:
```
results = nlc.nonlincausalitymeasureMLP(x=data_train, maxlag=lags, window=100, step=1, Dense_layers=2, Dense_neurons=[100, 100], x_test=data_test, run=5, add_Dropout=True, Dropout_rate=0.01, epochs_num=[50, 100], learning_rate=[0.001, 0.0001], batch_size_num=128, verbose=False, plot=True)
```
### Conditional causality
**nonlincausality** package also allows to study conditional causality (with signal Z).
```
results_conditional = nlc.nonlincausalityMLP(x=data_train, maxlag=lags, Dense_layers=2, Dense_neurons=[100, 100], x_test=data_test, run=5, add_Dropout=True, Dropout_rate=0.01, z=z_train, z_test=z_test, epochs_num=[50, 100], learning_rate=[0.001, 0.0001], batch_size_num=128, verbose=True, plot=True)
```
Raw data
{
"_id": null,
"home_page": "https://github.com/mrosol/Nonlincausality",
"name": "nonlincausality",
"maintainer": "",
"docs_url": null,
"requires_python": ">=3.6",
"maintainer_email": "",
"keywords": "Granger causality neural networks nonlinear forecasting signals",
"author": "Maciej Roso\u0142",
"author_email": "mrosol5@gmail.com",
"download_url": "https://files.pythonhosted.org/packages/26/a7/a59440c8f60d261f23b0c11bc40b32209236004716a5378bd024de641211/nonlincausality-1.1.10.tar.gz",
"platform": null,
"description": "# nonlincausality\n\nPython package for Granger causality test with nonlinear forecasting methods (neural networks).\n\nThis package contains two types of functions. \n\nAs a traditional Granger causality test is using linear regression for prediction it may not capture more complex causality relations.\nThe first type of presented functions are using nonlinear forecasting methods (neural networks) for prediction instead of linear regression. \nFor each tested lag this function is creating 2 models. The first one is forecasting the present value of X based on n=current lag past values of X, \nwhile the second model is forecasting the same value based on n=current lag past values of X and Y time series.\nIf the prediction error of the second model is statistically significantly smaller than the error of the first model then it means that Y is G-causing X (Y\u2794X).\nIt is also possible to test conditional causality using those functions.\nThe functions based on neural networks can test the causality on the given test set (which is recomended). The first type of function contains: `nonlincausalityMLP()`, `nonlincausalityLSTM()`, `nonlincausalityGRU()`, `nonlincausalityNN()` (and additionally `nonlincausalityARIMA()`, as there is no other Python implementation of ARIMA/ARIMAX models for causality analysis).\n\nThe second type of functions is for measuring the change of causality over time.\nThose functions are using first type functions to create the forecasting models.\nThey calculate the measure of the causality in a given time window (`w1`) with a given step (`w2`).\nThe measure of change of the causality over time is expressed by the equation:\n\n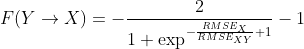\n\nThose functions can operate with multiple time series and test causal relations for each pair of signals.\nThe second type of function contains: `nonlincausalitymeasureMLP()`, `nonlincausalitymeasureLSTM()`, `nonlincausalitymeasureGRU()`, `nonlincausalitymeasureNN()` and `nonlincausalitymeasureARIMA()`.\n\n## Author\n**Maciej Roso\u0142**\nmrosol5@gmail.com, maciej.rosol.dokt@pw.edu.pl <br />\nWarsaw University of Technology\n\n## Reference \nMaciej Roso\u0142, Marcel M\u0142y\u0144czak, Gerard Cybulski <br />\nGranger causality test with nonlinear neural-network-based methods: Python package and simulation study. <br />\nComputer Methods and Programs in Biomedicine, Volume 216, 2022 <br />\nhttps://doi.org/10.1016/j.cmpb.2022.106669\n\n## Example usage\n\nAssume that there are two signals X and Y, which are stored in the variable `data`, where X is in the first column and Y in the second. The variable `data` was split into `data_train` (first 70% of the data) and `data_test` (last 30% of the data). Then to test the presence of causality Y\u2794X for the given lag values (defined as a list e.g. `[50, 150]`) the following functions can be used (all arguments are examples and may vary depending on the data.).\n\n### MLP\n```\nresults = nonlincausalityMLP(x=data_train, maxlag=lags, Dense_layers=2, Dense_neurons=[100, 100], x_test=data_test, run=1, add_Dropout=True, Dropout_rate=0.01, epochs_num=[50, 100], learning_rate=[0.001, 0.0001], batch_size_num=128, verbose=True, plot=True)\n```\n\n### GRU\n```\nresults_GRU = nonlincausalityGRU(x=data_train, maxlag=lags, GRU_layers=2, GRU_neurons=[25, 25], Dense_layers=2, Dense_neurons=[100, 100], x_test=data_test, run=3, add_Dropout=True, Dropout_rate=0.01, epochs_num=[50, 100], learning_rate=[0.001, 0.0001], batch_size_num=128, verbose=False, plot=True)\n```\n\n### LSTM\n```\nresults_LSTM = nonlincausalityLSTM(x=data_train, maxlag=lags, LSTM_layers=2, LSTM_neurons=[25, 25], Dense_layers=2, Dense_neurons=[100, 100], x_test=data_test, run=3, add_Dropout=True, Dropout_rate=0.01, epochs_num=[50, 100], learning_rate=[0.001, 0.0001], batch_size_num=128, verbose=False, plot=True)\n```\n\n### NN\n```\nresults_NN = nonlincausalityNN(x=data_train, maxlag=lags, NN_config=[\"l\", \"dr\", \"g\", \"dr\", \"d\", \"dr\"], NN_neurons=[5, 0.1, 5, 0.1, 5, 0.1], x_test=data_test, run=3, epochs_num=[50, 100], learning_rate=[0.001, 0.0001], batch_size_num=128, verbose=False, plot=True)\n```\n\n### ARIMA\n```\nresults_ARIMA = nonlincausalityARIMA(x=data_train, maxlag=lags, x_test=data_train)\n```\n\n### Change of causality over time\nFor a deeper understanding of the dependency between the signals, the change of causality over time might be studied using the above-mentioned functions. The example usage for MLP neural networks:\n```\nresults = nlc.nonlincausalitymeasureMLP(x=data_train, maxlag=lags, window=100, step=1, Dense_layers=2, Dense_neurons=[100, 100], x_test=data_test, run=5, add_Dropout=True, Dropout_rate=0.01, epochs_num=[50, 100], learning_rate=[0.001, 0.0001], batch_size_num=128, verbose=False, plot=True)\n```\n\n### Conditional causality\n**nonlincausality** package also allows to study conditional causality (with signal Z). \n```\nresults_conditional = nlc.nonlincausalityMLP(x=data_train, maxlag=lags, Dense_layers=2, Dense_neurons=[100, 100], x_test=data_test, run=5, add_Dropout=True, Dropout_rate=0.01, z=z_train, z_test=z_test, epochs_num=[50, 100], learning_rate=[0.001, 0.0001], batch_size_num=128, verbose=True, plot=True)\n```\n",
"bugtrack_url": null,
"license": "MIT",
"summary": "Python package for Granger causality test with nonlinear (neural networks) forecasting methods.",
"version": "1.1.10",
"split_keywords": [
"granger",
"causality",
"neural",
"networks",
"nonlinear",
"forecasting",
"signals"
],
"urls": [
{
"comment_text": "",
"digests": {
"md5": "2cc1067046602b4f7e2533bd1ea6ffda",
"sha256": "839fda159a587d748a770693e734dac47a57c35471d230fabc4e94f6796baf34"
},
"downloads": -1,
"filename": "nonlincausality-1.1.10-py3-none-any.whl",
"has_sig": false,
"md5_digest": "2cc1067046602b4f7e2533bd1ea6ffda",
"packagetype": "bdist_wheel",
"python_version": "py3",
"requires_python": ">=3.6",
"size": 20757,
"upload_time": "2022-12-12T12:05:52",
"upload_time_iso_8601": "2022-12-12T12:05:52.757563Z",
"url": "https://files.pythonhosted.org/packages/e0/43/680e7a8a1090d59d2f5aac38913a6a0c942eb621f988b96ecad0b081c1c5/nonlincausality-1.1.10-py3-none-any.whl",
"yanked": false,
"yanked_reason": null
},
{
"comment_text": "",
"digests": {
"md5": "9a126b28d9188e9b5427aacf6b5eb249",
"sha256": "5035b68004307947349ba288483593afa312b0746b17d44cce7c53d036ad4887"
},
"downloads": -1,
"filename": "nonlincausality-1.1.10.tar.gz",
"has_sig": false,
"md5_digest": "9a126b28d9188e9b5427aacf6b5eb249",
"packagetype": "sdist",
"python_version": "source",
"requires_python": ">=3.6",
"size": 20755,
"upload_time": "2022-12-12T12:06:06",
"upload_time_iso_8601": "2022-12-12T12:06:06.909905Z",
"url": "https://files.pythonhosted.org/packages/26/a7/a59440c8f60d261f23b0c11bc40b32209236004716a5378bd024de641211/nonlincausality-1.1.10.tar.gz",
"yanked": false,
"yanked_reason": null
}
],
"upload_time": "2022-12-12 12:06:06",
"github": true,
"gitlab": false,
"bitbucket": false,
"github_user": "mrosol",
"github_project": "Nonlincausality",
"travis_ci": false,
"coveralls": false,
"github_actions": false,
"lcname": "nonlincausality"
}
