`oplot` is a medley of various plotting and visualization functions, with
`matplotlib` and `seaborn` in the background.
# matrix.py
```python
import pandas as pd
from oplot import heatmap
d = pd.DataFrame(
[
{'A': 1, 'B': 3, 'C': 1},
{'A': 1, 'B': 3, 'C': 2},
{'A': 5, 'B': 5, 'C': 4},
{'A': 3, 'B': 2, 'C': 2},
{'A': 1, 'B': 3, 'C': 3},
{'A': 4, 'B': 3, 'C': 1},
{'A': 5, 'B': 1, 'C': 3},
]
)
heatmap(d)
```
<img src="https://user-images.githubusercontent.com/1906276/127305086-94c54108-4ff2-471d-b808-89e0ae0f51d9.png" width="320">
Lot's more control is available. Signature is
```python
(X, y=None, col_labels=None, figsize=None, cmap=None, return_gcf=False,
ax=None, xlabel_top=True, ylabel_left=True, xlabel_bottom=True,
ylabel_right=True, **kwargs)
```
# multiplots.py
The multiplots module contains functions to make "grid like" plot made of
several different plots. The main parameter is an iterator of functions, each
taking an ax as input and drawing something on it.
For example:
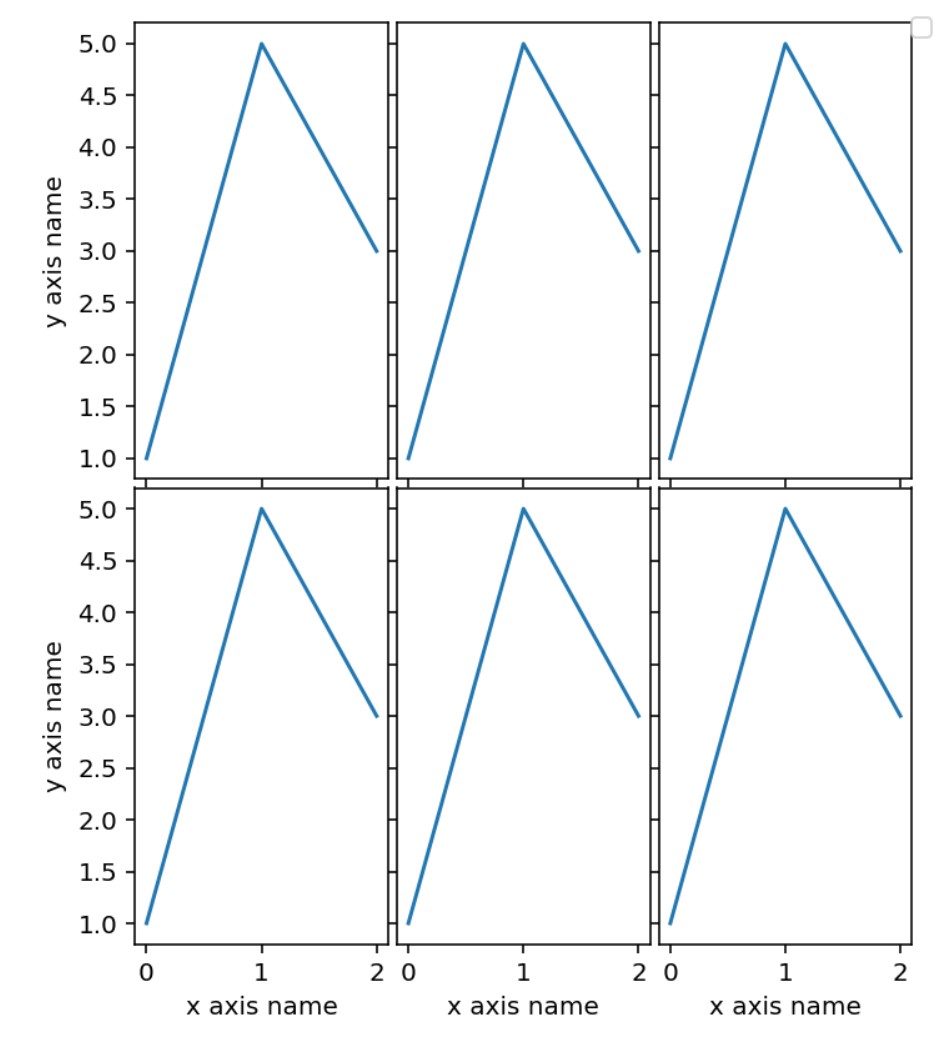 oplot import ax_func_to_plot
```python
# ax_func just takes a matplotlib axix and draws something on it
def ax_func(ax):
ax.plot([1, 5, 3])
# with an iterable of functions like ax_func, ax_func_to_plot makes
# a simple grid plot. The parameter n_per_row control the number of plots
# per row
ax_func_to_plot([ax_func] * 6,
n_per_row=3,
width=5,
height_row=3,
x_labels='x axis name',
y_labels='y axis name',
outer_axis_labels_only=True)
```
<img src="https://user-images.githubusercontent.com/1906276/127305797-948851fa-6cb0-4d19-aac1-6508ee7db04f.png" width="320">
In some cases, the number of plots on the grid may be large enough to exceed
the memory limit available to be saved on a single plot. In that case the function
multiplot_with_max_size comes handy. You can specify a parameter
max_plot_per_file, and if needed several plots with no more than that many
plots will be created.
# ui_scores_mapping.py
The module contains functions to make "sigmoid like" mappings. The original
and main intent is to provide function to map outlier scores to a bounded range,
typically (0, 10). The function look like a sigmoid but in reality is linear
over a predefined range, allowing for little "distortion" over a range of
particular interest.
```python
from oplot import make_ui_score_mapping
import numpy as np
# the map will be linear in the range 0 to 5. By default the range
# of the sigmoid will be (0, 10)
sigmoid_map = make_ui_score_mapping(min_lin_score=0, max_lin_score=5)
x = np.arange(-10, 15)
y = [sigmoid_map(i) for i in x]
plt.plot(x, y)
```
<img src="https://raw.githubusercontent.com/i2mint/oplot/master/readme_plots/Screen Shot 2021-01-06 at 07.21.26.png" width="320">
# outlier_scores.py
This module contains functions to plot outlier scores with colors corresponding
to chosen thresholds.
```python
from oplot import plot_scores_and_zones
scores = np.random.random(200)
plot_scores_and_zones(scores, zones=[0, 0.25, 0.5, 0.9])
```
<img src="https://raw.githubusercontent.com/i2mint/oplot/master/readme_plots/Screen_Shot_2021-01-06_at_08.32.16.png" width="320">
find_prop_markers, get_confusion_zone_percentiles and get_confusion_zones_std provides tools
to find statistically meaningfull zones.
# plot_audio.py
Here two functions of interest, plot_spectra which does what the name implies,
and plot_wf_and_spectro which gives two plots on top of each others:
a) the samples of wf over time
b) the aligned spectra
Parameters allows to add vertical markers to the plot like in the example below.
<img src="https://raw.githubusercontent.com/i2mint/oplot/master/readme_plots/Screen_Shot_2021-01-06_at_09.08.55.png" width="800">
# plot_data_set.py
## density_distribution
Plots the density distribution of different data sets (arrays).
Example of a data dict with data having two different distributions:
```python
data_dict = {
'Unicorn Heights': np.random.normal(loc=6, scale=1, size=1000),
'Dragon Wingspan': np.concatenate(
[
np.random.normal(loc=3, scale=0.5, size=500),
np.random.normal(loc=7, scale=0.5, size=500),
]
),
}
```
Plot this with all the defaults:
```python
density_distribution(data_dict)
```

Plot this with a bunch of configurations:
```python
from matplotlib import pyplot as plt
# Plot with customized arguments
fig, ax = plt.subplots(figsize=(10, 6))
density_distribution(
data_dict,
ax=ax,
axvline_kwargs={
'Unicorn Heights': {'color': 'magenta', 'linestyle': ':'},
'Dragon Wingspan': {'color': 'cyan', 'linestyle': '-.'},
},
line_width=2,
location_linestyle='-.',
colors=('magenta', 'cyan'),
density_plot_func=sns.histplot,
density_plot_kwargs={'fill': True},
text_kwargs={'x': 0.1, 'y': 0.9, 'bbox': dict(facecolor='yellow', alpha=0.5)},
mean_line_kwargs={'linewidth': 2},
)
ax.set_title('Customized Density Plot')
plt.show()
```

## scatter_and_color_according_to_y
Next, we have a look at `scatter_and_color_according_to_y`, which makes a 2d
or 3d scatter plot with color representing the class. The dimension reduction
is controled by the paramters projection and dim_reduct.
from oplot.plot_data_set import scatter_and_color_according_to_y
from sklearn.datasets import make_classification
```python
from oplot import scatter_and_color_according_to_y
X, y = make_classification(n_samples=500,
n_features=20,
n_classes=4,
n_clusters_per_class=1)
scatter_and_color_according_to_y(X, y,
projection='2d',
dim_reduct='PCA')
```
<img src="https://raw.githubusercontent.com/i2mint/oplot/master/readme_plots/Screen_Shot_2021-01-06_at_11.36.02.png" width="320">
```python
from oplot import scatter_and_color_according_to_y
scatter_and_color_according_to_y(X, y,
projection='3d',
dim_reduct='LDA')
```
<img src="https://raw.githubusercontent.com/i2mint/oplot/master/readme_plots/Screen_Shot_2021-01-06_at_11.36.07.png" width="320">
There is also that little one, which I don't remeber ever using and needs some work:
```python
from oplot import side_by_side_bar
side_by_side_bar([[1,2,3], [4,5,6]], list_names=['you', 'me'])
```
<img src="https://raw.githubusercontent.com/i2mint/oplot/master/readme_plots/Screen_Shot_2021-01-06_at_11.56.42.png" width="320">
## plot_stats.py
This module contains functions to plot statistics about datasets or model
results.
The confusion matrix is a classic easy one, below is a modification of an
sklearn function:
```python
from oplot.plot_stats import plot_confusion_matrix
from sklearn.datasets import make_classification
X, truth = make_classification(n_samples=500,
n_features=20,
n_classes=4,
n_clusters_per_class=1)
# making a copy of truth and messing with it
y = truth.copy()
y[:50] = (y[:50] + 1) % 4
plot_confusion_matrix(y, truth)
```
<img src="https://raw.githubusercontent.com/i2mint/oplot/master/readme_plots/Screen_Shot_2021-01-06_at_12.59.52.png" width="320">
`make_normal_outlier_timeline` plots the scores with a color/legend given by
the aligned list truth
```python
from oplot.plot_stats import make_normal_outlier_timeline
scores = np.arange(-1, 3, 0.1)
tags = np.array(['normal'] * 20 + ['outlier'] * 15 + ['crazy'] * (len(scores) - 20 - 15))
make_normal_outlier_timeline(tags, scores)
```
<img src="https://raw.githubusercontent.com/i2mint/oplot/master/readme_plots/Screen_Shot_2021-01-07_at_05.46.39.png" width="800">
`make_tables_tn_fp_fn_tp` is convenient to obtain True Positive and False Negative
tables. The range of thresholds is induced from the data.
```python
from oplot.plot_stats import make_tables_tn_fp_fn_tp
scores = np.arange(-1, 3, 0.1)
truth = scores > 2.5
make_tables_tn_fp_fn_tp(truth, scores)
```
<img src="https://raw.githubusercontent.com/i2mint/oplot/master/readme_plots/Screen_Shot_2021-01-07_at_05.51.23.png" width="320">
`render_mpl_table` takes any pandas dataframe and turn it into a pretty plot
which can then be saved as a pdf for example.
```python
from oplot.plot_stats import make_tables_tn_fp_fn_tp, render_mpl_table
scores = np.arange(-1, 3, 0.1)
truth = scores > 2.5
df = make_tables_tn_fp_fn_tp(truth, scores)
render_mpl_table(df)
```
<img src="https://raw.githubusercontent.com/i2mint/oplot/master/readme_plots/Screen_Shot_2021-01-07_at_05.54.23.png" width="320">
`plot_outlier_metric_curve` plots ROC type. You specify which pair of statistics
you want to display along with a list of scores and truth (0 for negative, 1 for positive).
The chance line is computed and displayed by default and the total area is returned.
```python
from oplot.plot_stats import plot_outlier_metric_curve
# list of scores with higher average scores for positive events
scores = np.concatenate([np.random.random(100), np.random.random(100) * 2])
truth = np.array([0] * 100 + [1] * 100)
pair_metrics={'x': 'recall', 'y': 'precision'}
plot_outlier_metric_curve(truth, scores,
pair_metrics=pair_metrics)
```
<img src="https://raw.githubusercontent.com/i2mint/oplot/master/readme_plots/Screen_Shot_2021-01-07_at_06.04.52.png" width="320">
There are many choices for the statistics to display, some pairs making more or
less sense, some not at all.
```python
from oplot.plot_stats import plot_outlier_metric_curve
pair_metrics={'x': 'false_positive_rate', 'y': 'false_negative_rate'}
plot_outlier_metric_curve(truth, scores,
pair_metrics=pair_metrics)
```
<img src="https://raw.githubusercontent.com/i2mint/oplot/master/readme_plots/Screen_Shot_2021-01-07_at_06.11.13.png" width="320">
The full list of usable statistics along with synonymous:
```python
# all these scores except for MCC gives a score between 0 and 1.
# I normalized MMC into what I call NNMC in order to keep the same scale for all.
base_statistics_dict = {'TPR': lambda tn, fp, fn, tp: tp / (tp + fn),
# sensitivity, recall, hit rate, or true positive rate
'TNR': lambda tn, fp, fn, tp: tn / (tn + fp), # specificity, selectivity or true negative rate
'PPV': lambda tn, fp, fn, tp: tp / (tp + fp), # precision or positive predictive value
'NPV': lambda tn, fp, fn, tp: tn / (tn + fn), # negative predictive value
'FNR': lambda tn, fp, fn, tp: fn / (fn + tp), # miss rate or false negative rate
'FPR': lambda tn, fp, fn, tp: fp / (fp + tn), # fall-out or false positive rate
'FDR': lambda tn, fp, fn, tp: fp / (fp + tp), # false discovery rate
'FOR': lambda tn, fp, fn, tp: fn / (fn + tn), # false omission rate
'TS': lambda tn, fp, fn, tp: tp / (tp + fn + fp),
# threat score (TS) or Critical Success Index (CSI)
'ACC': lambda tn, fp, fn, tp: (tp + tn) / (tp + tn + fp + fn), # accuracy
'F1': lambda tn, fp, fn, tp: (2 * tp) / (2 * tp + fp + fn), # F1 score
'NMCC': lambda tn, fp, fn, tp: ((tp * tn - fp * fn) / (
(tp + fp) * (tp + fn) * (tn + fp) * (tn + fn)) ** 0.5 + 1) / 2,
# NORMALIZED TO BE BETWEEN 0 AND 1 Matthews correlation coefficient
'BM': lambda tn, fp, fn, tp: tp / (tp + fn) + tn / (tn + fp) - 1,
# Informedness or Bookmaker Informedness
'MK': lambda tn, fp, fn, tp: tp / (tp + fp) + tn / (tn + fn) - 1} # Markedness
synonyms = {'TPR': ['recall', 'sensitivity', 'true_positive_rate', 'hit_rate', 'tpr'],
'TNR': ['specificity', 'SPC', 'true_negative_rate', 'selectivity', 'tnr'],
'PPV': ['precision', 'positive_predictive_value', 'ppv'],
'NPV': ['negative_predictive_value', 'npv'],
'FNR': ['miss_rate', 'false_negative_rate', 'fnr'],
'FPR': ['fall_out', 'false_positive_rate', 'fpr'],
'FDR': ['false_discovery_rate', 'fdr'],
'FOR': ['false_omission_rate', 'for'],
'TS': ['threat_score', 'critical_success_index', 'CSI', 'csi', 'ts'],
'ACC': ['accuracy', 'acc'],
'F1': ['f1_score', 'f1', 'F1_score'],
'NMCC': ['normalized_Matthews_correlation_coefficient', 'nmcc'],
'BM': ['informedness', 'bookmaker_informedness', 'bi', 'BI', 'bm'],
'MK': ['markedness', 'mk']}
```
# Ploting Distributions/Density
Testing the kdeplot_w_boundary_condition Function
This section provides sample code to test the kdeplot_w_boundary_condition function with data drawn from two Gaussian distributions, using a boundary condition lambda X, Y: Y <= X.
## Generate some data to test on
```python
import numpy as np
import pandas as pd
# Set random seed for reproducibility
np.random.seed(42)
# Parameters for the first Gaussian blob
mean1 = [0, 0]
cov1 = [[1, 0.5], [0.5, 1]] # Positive correlation
# Parameters for the second Gaussian blob
mean2 = [4, 4]
cov2 = [[1, -0.3], [-0.3, 1]] # Slight negative correlation
# Number of samples per blob
n_samples = 500
# Generate samples for the first blob
x1, y1 = np.random.multivariate_normal(mean1, cov1, n_samples).T
# Generate samples for the second blob
x2, y2 = np.random.multivariate_normal(mean2, cov2, n_samples).T
# Combine the data
x = np.concatenate([x1, x2])
y = np.concatenate([y1, y2])
# Create a DataFrame
data = pd.DataFrame({'x': x, 'y': y})
```
## Plot with Boundary Condition `y ≤ x`
```python
from oplot import kdeplot_w_boundary_condition
import matplotlib.pyplot as plt
# Define the boundary condition function
boundary_condition = lambda X, Y: Y <= X
# Plot using the custom KDE function
ax = kdeplot_w_boundary_condition(
data=data,
x='x',
y='y',
boundary_condition=boundary_condition,
fill=True,
cmap='viridis',
figsize=(8, 6),
levels=15 # Increased levels for better resolution
)
# Add a title
ax.set_title('KDE Plot with Boundary Condition: y ≤ x')
# Show the plot
plt.show()
```
<img src="https://github.com/user-attachments/assets/4c67d06f-0907-4a9e-9b95-2f12870a205e" width="400">
## Plot Without Boundary Condition
```python
ax = kdeplot_w_boundary_condition(
data=data,
x='x',
y='y',
boundary_condition=None, # No boundary condition
fill=True,
cmap='viridis',
figsize=(8, 6),
levels=15
)
# Add a title
ax.set_title('KDE Plot without Boundary Condition')
# Show the plot
plt.show()
```
<img src="https://github.com/user-attachments/assets/8ea779cf-7dc0-4aae-a3e1-194abf2046bd" width="400">
### Output
When you run the code above, you will get two plots:
1. With Boundary Condition: The KDE plot will display density only in regions where `y ≤ x`, effectively masking out areas where `y > x`.
2. Without Boundary Condition: The KDE plot will display the density over the entire range of the data, showing both Gaussian blobs fully.
Additional Tests with Different Boundary Conditions
## Boundary Condition `y ≥ x`
```python
# Define a different boundary condition function
boundary_condition = lambda X, Y: Y >= X
# Plot using the custom KDE function
ax = kdeplot_w_boundary_condition(
data=data,
x='x',
y='y',
boundary_condition=boundary_condition,
fill=True,
cmap='coolwarm',
figsize=(8, 6),
levels=15
)
# Add a title
ax.set_title('KDE Plot with Boundary Condition: y ≥ x')
# Show the plot
plt.show()
```
<img src="https://github.com/user-attachments/assets/32d06bc2-cd9f-4680-88ec-5dd3d9a79abd" width="400">
## Circular Boundary Condition
```python
# Define a circular boundary condition function
boundary_condition = lambda X, Y: (X - 2)**2 + (Y - 2)**2 <= 3**2
# Plot using the custom KDE function
ax = kdeplot_w_boundary_condition(
data=data,
x='x',
y='y',
boundary_condition=boundary_condition,
fill=True,
cmap='plasma',
figsize=(8, 6),
levels=15
)
# Add a title
ax.set_title('KDE Plot with Circular Boundary Condition')
# Show the plot
plt.show()
```
<img src="https://github.com/user-attachments/assets/e28fe762-98fe-4401-8c69-0863d176da78" width="400">
Raw data
{
"_id": null,
"home_page": "https://github.com/otosense/oplot",
"name": "oplot",
"maintainer": null,
"docs_url": null,
"requires_python": null,
"maintainer_email": null,
"keywords": null,
"author": "OtoSense",
"author_email": null,
"download_url": "https://files.pythonhosted.org/packages/29/46/392bb96182d2aec830d7a27d92e9977b7e68932cf412978e2132406e490b/oplot-0.1.25.tar.gz",
"platform": "any",
"description": "`oplot` is a medley of various plotting and visualization functions, with \n`matplotlib` and `seaborn` in the background.\n\n\n# matrix.py\n\n```python\nimport pandas as pd\nfrom oplot import heatmap \nd = pd.DataFrame(\n [\n {'A': 1, 'B': 3, 'C': 1},\n {'A': 1, 'B': 3, 'C': 2},\n {'A': 5, 'B': 5, 'C': 4},\n {'A': 3, 'B': 2, 'C': 2},\n {'A': 1, 'B': 3, 'C': 3},\n {'A': 4, 'B': 3, 'C': 1},\n {'A': 5, 'B': 1, 'C': 3},\n ]\n)\nheatmap(d)\n```\n\n<img src=\"https://user-images.githubusercontent.com/1906276/127305086-94c54108-4ff2-471d-b808-89e0ae0f51d9.png\" width=\"320\">\n\nLot's more control is available. Signature is\n\n```python\n(X, y=None, col_labels=None, figsize=None, cmap=None, return_gcf=False, \nax=None, xlabel_top=True, ylabel_left=True, xlabel_bottom=True, \nylabel_right=True, **kwargs)\n\n```\n\n# multiplots.py\n\nThe multiplots module contains functions to make \"grid like\" plot made of \nseveral different plots. The main parameter is an iterator of functions, each \ntaking an ax as input and drawing something on it.\n\nFor example:\n\n oplot import ax_func_to_plot\n\n```python\n# ax_func just takes a matplotlib axix and draws something on it\ndef ax_func(ax):\n ax.plot([1, 5, 3])\n\n# with an iterable of functions like ax_func, ax_func_to_plot makes \n# a simple grid plot. The parameter n_per_row control the number of plots \n# per row\nax_func_to_plot([ax_func] * 6,\n n_per_row=3,\n width=5,\n height_row=3,\n x_labels='x axis name',\n y_labels='y axis name',\n outer_axis_labels_only=True)\n```\n\n<img src=\"https://user-images.githubusercontent.com/1906276/127305797-948851fa-6cb0-4d19-aac1-6508ee7db04f.png\" width=\"320\">\n\nIn some cases, the number of plots on the grid may be large enough to exceed\nthe memory limit available to be saved on a single plot. In that case the function\nmultiplot_with_max_size comes handy. You can specify a parameter\nmax_plot_per_file, and if needed several plots with no more than that many\nplots will be created.\n\n\n# ui_scores_mapping.py\n\nThe module contains functions to make \"sigmoid like\" mappings. The original \nand main intent is to provide function to map outlier scores to a bounded range,\ntypically (0, 10). The function look like a sigmoid but in reality is linear \nover a predefined range, allowing for little \"distortion\" over a range of\nparticular interest.\n\n\n```python\nfrom oplot import make_ui_score_mapping\nimport numpy as np\n\n# the map will be linear in the range 0 to 5. By default the range\n# of the sigmoid will be (0, 10)\nsigmoid_map = make_ui_score_mapping(min_lin_score=0, max_lin_score=5)\n\nx = np.arange(-10, 15)\ny = [sigmoid_map(i) for i in x]\n\nplt.plot(x, y)\n```\n\n<img src=\"https://raw.githubusercontent.com/i2mint/oplot/master/readme_plots/Screen Shot 2021-01-06 at 07.21.26.png\" width=\"320\">\n\n\n# outlier_scores.py\n\nThis module contains functions to plot outlier scores with colors corresponding\nto chosen thresholds.\n\n```python\nfrom oplot import plot_scores_and_zones\n\nscores = np.random.random(200)\nplot_scores_and_zones(scores, zones=[0, 0.25, 0.5, 0.9])\n```\n<img src=\"https://raw.githubusercontent.com/i2mint/oplot/master/readme_plots/Screen_Shot_2021-01-06_at_08.32.16.png\" width=\"320\">\n\nfind_prop_markers, get_confusion_zone_percentiles and get_confusion_zones_std provides tools\nto find statistically meaningfull zones.\n\n\n# plot_audio.py\n\nHere two functions of interest, plot_spectra which does what the name implies,\nand plot_wf_and_spectro which gives two plots on top of each others:\n\na) the samples of wf over time\n\nb) the aligned spectra\n\nParameters allows to add vertical markers to the plot like in the example below.\n\n<img src=\"https://raw.githubusercontent.com/i2mint/oplot/master/readme_plots/Screen_Shot_2021-01-06_at_09.08.55.png\" width=\"800\">\n\n\n# plot_data_set.py\n\n\n## density_distribution\n\n Plots the density distribution of different data sets (arrays).\n\nExample of a data dict with data having two different distributions:\n\n```python\ndata_dict = {\n 'Unicorn Heights': np.random.normal(loc=6, scale=1, size=1000),\n 'Dragon Wingspan': np.concatenate(\n [\n np.random.normal(loc=3, scale=0.5, size=500),\n np.random.normal(loc=7, scale=0.5, size=500),\n ]\n ),\n}\n```\n\nPlot this with all the defaults:\n\n```python\ndensity_distribution(data_dict)\n```\n\n\n\n\nPlot this with a bunch of configurations:\n\n```python\nfrom matplotlib import pyplot as plt\n\n# Plot with customized arguments\nfig, ax = plt.subplots(figsize=(10, 6))\ndensity_distribution(\n data_dict,\n ax=ax,\n axvline_kwargs={\n 'Unicorn Heights': {'color': 'magenta', 'linestyle': ':'},\n 'Dragon Wingspan': {'color': 'cyan', 'linestyle': '-.'},\n },\n line_width=2,\n location_linestyle='-.',\n colors=('magenta', 'cyan'),\n density_plot_func=sns.histplot,\n density_plot_kwargs={'fill': True},\n text_kwargs={'x': 0.1, 'y': 0.9, 'bbox': dict(facecolor='yellow', alpha=0.5)},\n mean_line_kwargs={'linewidth': 2},\n)\nax.set_title('Customized Density Plot')\nplt.show()\n```\n\n\n\n\n\n## scatter_and_color_according_to_y\n\nNext, we have a look at `scatter_and_color_according_to_y`, which makes a 2d\nor 3d scatter plot with color representing the class. The dimension reduction \nis controled by the paramters projection and dim_reduct.\n\nfrom oplot.plot_data_set import scatter_and_color_according_to_y\nfrom sklearn.datasets import make_classification\n\n```python\nfrom oplot import scatter_and_color_according_to_y\n\nX, y = make_classification(n_samples=500,\n n_features=20,\n n_classes=4,\n n_clusters_per_class=1)\n\nscatter_and_color_according_to_y(X, y,\n projection='2d',\n dim_reduct='PCA')\n```\n\n\n\n<img src=\"https://raw.githubusercontent.com/i2mint/oplot/master/readme_plots/Screen_Shot_2021-01-06_at_11.36.02.png\" width=\"320\">\n\n```python\nfrom oplot import scatter_and_color_according_to_y\n\nscatter_and_color_according_to_y(X, y,\n projection='3d',\n dim_reduct='LDA')\n```\n\n\n<img src=\"https://raw.githubusercontent.com/i2mint/oplot/master/readme_plots/Screen_Shot_2021-01-06_at_11.36.07.png\" width=\"320\">\n\nThere is also that little one, which I don't remeber ever using and needs some work:\n\n```python\nfrom oplot import side_by_side_bar\n\nside_by_side_bar([[1,2,3], [4,5,6]], list_names=['you', 'me'])\n```\n\n<img src=\"https://raw.githubusercontent.com/i2mint/oplot/master/readme_plots/Screen_Shot_2021-01-06_at_11.56.42.png\" width=\"320\">\n\n\n## plot_stats.py\n\nThis module contains functions to plot statistics about datasets or model\nresults.\nThe confusion matrix is a classic easy one, below is a modification of an\nsklearn function:\n\n```python\nfrom oplot.plot_stats import plot_confusion_matrix\nfrom sklearn.datasets import make_classification\n\nX, truth = make_classification(n_samples=500,\n n_features=20,\n n_classes=4,\n n_clusters_per_class=1)\n \n# making a copy of truth and messing with it\ny = truth.copy()\ny[:50] = (y[:50] + 1) % 4\n\nplot_confusion_matrix(y, truth)\n```\n\n<img src=\"https://raw.githubusercontent.com/i2mint/oplot/master/readme_plots/Screen_Shot_2021-01-06_at_12.59.52.png\" width=\"320\">\n\n`make_normal_outlier_timeline` plots the scores with a color/legend given by\nthe aligned list truth\n\n```python\nfrom oplot.plot_stats import make_normal_outlier_timeline\n\nscores = np.arange(-1, 3, 0.1)\ntags = np.array(['normal'] * 20 + ['outlier'] * 15 + ['crazy'] * (len(scores) - 20 - 15))\nmake_normal_outlier_timeline(tags, scores)\n```\n\n<img src=\"https://raw.githubusercontent.com/i2mint/oplot/master/readme_plots/Screen_Shot_2021-01-07_at_05.46.39.png\" width=\"800\">\n\n\n`make_tables_tn_fp_fn_tp` is convenient to obtain True Positive and False Negative\ntables. The range of thresholds is induced from the data.\n\n```python\nfrom oplot.plot_stats import make_tables_tn_fp_fn_tp\n\nscores = np.arange(-1, 3, 0.1)\ntruth = scores > 2.5\nmake_tables_tn_fp_fn_tp(truth, scores)\n```\n\n<img src=\"https://raw.githubusercontent.com/i2mint/oplot/master/readme_plots/Screen_Shot_2021-01-07_at_05.51.23.png\" width=\"320\">\n\n`render_mpl_table` takes any pandas dataframe and turn it into a pretty plot \nwhich can then be saved as a pdf for example.\n\n```python\nfrom oplot.plot_stats import make_tables_tn_fp_fn_tp, render_mpl_table\n\nscores = np.arange(-1, 3, 0.1)\ntruth = scores > 2.5\ndf = make_tables_tn_fp_fn_tp(truth, scores)\nrender_mpl_table(df)\n```\n<img src=\"https://raw.githubusercontent.com/i2mint/oplot/master/readme_plots/Screen_Shot_2021-01-07_at_05.54.23.png\" width=\"320\">\n\n`plot_outlier_metric_curve` plots ROC type. You specify which pair of statistics\nyou want to display along with a list of scores and truth (0 for negative, 1 for positive).\nThe chance line is computed and displayed by default and the total area is returned.\n\n```python\nfrom oplot.plot_stats import plot_outlier_metric_curve\n\n# list of scores with higher average scores for positive events\nscores = np.concatenate([np.random.random(100), np.random.random(100) * 2])\ntruth = np.array([0] * 100 + [1] * 100)\n\npair_metrics={'x': 'recall', 'y': 'precision'}\nplot_outlier_metric_curve(truth, scores,\n pair_metrics=pair_metrics)\n```\n\n<img src=\"https://raw.githubusercontent.com/i2mint/oplot/master/readme_plots/Screen_Shot_2021-01-07_at_06.04.52.png\" width=\"320\">\n\n\nThere are many choices for the statistics to display, some pairs making more or\nless sense, some not at all.\n\n```python\nfrom oplot.plot_stats import plot_outlier_metric_curve\n\npair_metrics={'x': 'false_positive_rate', 'y': 'false_negative_rate'}\nplot_outlier_metric_curve(truth, scores,\n pair_metrics=pair_metrics)\n```\n\n<img src=\"https://raw.githubusercontent.com/i2mint/oplot/master/readme_plots/Screen_Shot_2021-01-07_at_06.11.13.png\" width=\"320\">\n\n\n\n\nThe full list of usable statistics along with synonymous:\n\n```python\n# all these scores except for MCC gives a score between 0 and 1.\n# I normalized MMC into what I call NNMC in order to keep the same scale for all.\nbase_statistics_dict = {'TPR': lambda tn, fp, fn, tp: tp / (tp + fn),\n # sensitivity, recall, hit rate, or true positive rate\n 'TNR': lambda tn, fp, fn, tp: tn / (tn + fp), # specificity, selectivity or true negative rate\n 'PPV': lambda tn, fp, fn, tp: tp / (tp + fp), # precision or positive predictive value\n 'NPV': lambda tn, fp, fn, tp: tn / (tn + fn), # negative predictive value\n 'FNR': lambda tn, fp, fn, tp: fn / (fn + tp), # miss rate or false negative rate\n 'FPR': lambda tn, fp, fn, tp: fp / (fp + tn), # fall-out or false positive rate\n 'FDR': lambda tn, fp, fn, tp: fp / (fp + tp), # false discovery rate\n 'FOR': lambda tn, fp, fn, tp: fn / (fn + tn), # false omission rate\n 'TS': lambda tn, fp, fn, tp: tp / (tp + fn + fp),\n # threat score (TS) or Critical Success Index (CSI)\n 'ACC': lambda tn, fp, fn, tp: (tp + tn) / (tp + tn + fp + fn), # accuracy\n 'F1': lambda tn, fp, fn, tp: (2 * tp) / (2 * tp + fp + fn), # F1 score\n 'NMCC': lambda tn, fp, fn, tp: ((tp * tn - fp * fn) / (\n (tp + fp) * (tp + fn) * (tn + fp) * (tn + fn)) ** 0.5 + 1) / 2,\n # NORMALIZED TO BE BETWEEN 0 AND 1 Matthews correlation coefficient\n 'BM': lambda tn, fp, fn, tp: tp / (tp + fn) + tn / (tn + fp) - 1,\n # Informedness or Bookmaker Informedness\n 'MK': lambda tn, fp, fn, tp: tp / (tp + fp) + tn / (tn + fn) - 1} # Markedness\n\nsynonyms = {'TPR': ['recall', 'sensitivity', 'true_positive_rate', 'hit_rate', 'tpr'],\n 'TNR': ['specificity', 'SPC', 'true_negative_rate', 'selectivity', 'tnr'],\n 'PPV': ['precision', 'positive_predictive_value', 'ppv'],\n 'NPV': ['negative_predictive_value', 'npv'],\n 'FNR': ['miss_rate', 'false_negative_rate', 'fnr'],\n 'FPR': ['fall_out', 'false_positive_rate', 'fpr'],\n 'FDR': ['false_discovery_rate', 'fdr'],\n 'FOR': ['false_omission_rate', 'for'],\n 'TS': ['threat_score', 'critical_success_index', 'CSI', 'csi', 'ts'],\n 'ACC': ['accuracy', 'acc'],\n 'F1': ['f1_score', 'f1', 'F1_score'],\n 'NMCC': ['normalized_Matthews_correlation_coefficient', 'nmcc'],\n 'BM': ['informedness', 'bookmaker_informedness', 'bi', 'BI', 'bm'],\n 'MK': ['markedness', 'mk']}\n```\n\n\n# Ploting Distributions/Density\n\n\nTesting the kdeplot_w_boundary_condition Function\n\nThis section provides sample code to test the kdeplot_w_boundary_condition function with data drawn from two Gaussian distributions, using a boundary condition lambda X, Y: Y <= X.\n\n## Generate some data to test on\n\n```python\nimport numpy as np\nimport pandas as pd\n\n# Set random seed for reproducibility\nnp.random.seed(42)\n\n# Parameters for the first Gaussian blob\nmean1 = [0, 0]\ncov1 = [[1, 0.5], [0.5, 1]] # Positive correlation\n\n# Parameters for the second Gaussian blob\nmean2 = [4, 4]\ncov2 = [[1, -0.3], [-0.3, 1]] # Slight negative correlation\n\n# Number of samples per blob\nn_samples = 500\n\n# Generate samples for the first blob\nx1, y1 = np.random.multivariate_normal(mean1, cov1, n_samples).T\n\n# Generate samples for the second blob\nx2, y2 = np.random.multivariate_normal(mean2, cov2, n_samples).T\n\n# Combine the data\nx = np.concatenate([x1, x2])\ny = np.concatenate([y1, y2])\n\n# Create a DataFrame\ndata = pd.DataFrame({'x': x, 'y': y})\n```\n\n## Plot with Boundary Condition `y \u2264 x`\n\n```python\nfrom oplot import kdeplot_w_boundary_condition\nimport matplotlib.pyplot as plt\n\n# Define the boundary condition function\nboundary_condition = lambda X, Y: Y <= X\n\n# Plot using the custom KDE function\nax = kdeplot_w_boundary_condition(\n data=data,\n x='x',\n y='y',\n boundary_condition=boundary_condition,\n fill=True,\n cmap='viridis',\n figsize=(8, 6),\n levels=15 # Increased levels for better resolution\n)\n\n# Add a title\nax.set_title('KDE Plot with Boundary Condition: y \u2264 x')\n\n# Show the plot\nplt.show()\n```\n\n<img src=\"https://github.com/user-attachments/assets/4c67d06f-0907-4a9e-9b95-2f12870a205e\" width=\"400\">\n\n\n## Plot Without Boundary Condition\n\n\n```python\nax = kdeplot_w_boundary_condition(\n data=data,\n x='x',\n y='y',\n boundary_condition=None, # No boundary condition\n fill=True,\n cmap='viridis',\n figsize=(8, 6),\n levels=15\n)\n\n# Add a title\nax.set_title('KDE Plot without Boundary Condition')\n\n# Show the plot\nplt.show()\n```\n\n\n<img src=\"https://github.com/user-attachments/assets/8ea779cf-7dc0-4aae-a3e1-194abf2046bd\" width=\"400\">\n\n\n### Output\n\nWhen you run the code above, you will get two plots:\n\t1.\tWith Boundary Condition: The KDE plot will display density only in regions where `y \u2264 x`, effectively masking out areas where `y > x`.\n\t2.\tWithout Boundary Condition: The KDE plot will display the density over the entire range of the data, showing both Gaussian blobs fully.\n\nAdditional Tests with Different Boundary Conditions\n\n## Boundary Condition `y \u2265 x`\n\n```python\n# Define a different boundary condition function\nboundary_condition = lambda X, Y: Y >= X\n\n# Plot using the custom KDE function\nax = kdeplot_w_boundary_condition(\n data=data,\n x='x',\n y='y',\n boundary_condition=boundary_condition,\n fill=True,\n cmap='coolwarm',\n figsize=(8, 6),\n levels=15\n)\n\n# Add a title\nax.set_title('KDE Plot with Boundary Condition: y \u2265 x')\n\n# Show the plot\nplt.show()\n```\n\n\n<img src=\"https://github.com/user-attachments/assets/32d06bc2-cd9f-4680-88ec-5dd3d9a79abd\" width=\"400\">\n\n\n## Circular Boundary Condition\n\n\n```python\n# Define a circular boundary condition function\nboundary_condition = lambda X, Y: (X - 2)**2 + (Y - 2)**2 <= 3**2\n\n# Plot using the custom KDE function\nax = kdeplot_w_boundary_condition(\n data=data,\n x='x',\n y='y',\n boundary_condition=boundary_condition,\n fill=True,\n cmap='plasma',\n figsize=(8, 6),\n levels=15\n)\n\n# Add a title\nax.set_title('KDE Plot with Circular Boundary Condition')\n\n# Show the plot\nplt.show()\n```\n\n<img src=\"https://github.com/user-attachments/assets/e28fe762-98fe-4401-8c69-0863d176da78\" width=\"400\">",
"bugtrack_url": null,
"license": "apache-2.0",
"summary": "A medley of plotting tools for data analysis",
"version": "0.1.25",
"project_urls": {
"Homepage": "https://github.com/otosense/oplot"
},
"split_keywords": [],
"urls": [
{
"comment_text": "",
"digests": {
"blake2b_256": "2946392bb96182d2aec830d7a27d92e9977b7e68932cf412978e2132406e490b",
"md5": "4d21b1c5b1bd89202c1773f048f254a1",
"sha256": "530ddd5228637467d01f72a08cf09108f02d90d1c8f544b33c2a4bf1ee2e43d1"
},
"downloads": -1,
"filename": "oplot-0.1.25.tar.gz",
"has_sig": false,
"md5_digest": "4d21b1c5b1bd89202c1773f048f254a1",
"packagetype": "sdist",
"python_version": "source",
"requires_python": null,
"size": 50421,
"upload_time": "2024-11-15T12:23:30",
"upload_time_iso_8601": "2024-11-15T12:23:30.964049Z",
"url": "https://files.pythonhosted.org/packages/29/46/392bb96182d2aec830d7a27d92e9977b7e68932cf412978e2132406e490b/oplot-0.1.25.tar.gz",
"yanked": false,
"yanked_reason": null
}
],
"upload_time": "2024-11-15 12:23:30",
"github": true,
"gitlab": false,
"bitbucket": false,
"codeberg": false,
"github_user": "otosense",
"github_project": "oplot",
"travis_ci": false,
"coveralls": false,
"github_actions": true,
"lcname": "oplot"
}
