<p align="center">
<a href="https://github.com/nschloe/optimesh"><img alt="optimesh" src="https://raw.githubusercontent.com/meshpro/optimesh/assets/optimesh-logo.svg" width="60%"></a>
<p align="center">Triangular mesh optimization.</p>
</p>
[](https://pypi.org/project/optimesh/)
[](https://pypi.org/project/optimesh/)
[](https://doi.org/10.5281/zenodo.4728056)
[](https://github.com/nschloe/optimesh)
[](https://pypistats.org/packages/optimesh)
[](https://discord.gg/PBCCvwHqpv)
Several mesh smoothing/optimization methods with one simple interface. optimesh
- is fast,
- preserves submeshes,
- only works for triangular meshes, flat and on a surface, (for now; upvote [this
issue](https://github.com/nschloe/optimesh/issues/17) if you're interested in
tetrahedral mesh smoothing), and
- supports all mesh formats that [meshio](https://github.com/nschloe/meshio) can
handle.
### Installation
Install optimesh [from PyPI](https://pypi.org/project/optimesh/) with
```
pip install optimesh
```
### How to get a license
Licenses for personal and academic use can be purchased
[here](https://buy.stripe.com/5kA3eV8t8af83iE9AE).
You'll receive a confirmation email with a license key.
Install the key with
```
slim install <your-license-key>
```
on your machine and you're good to go.
For commercial use, please contact support@mondaytech.com.
### Using optimesh
Example call:
```
optimesh in.e out.vtk
```
Output:
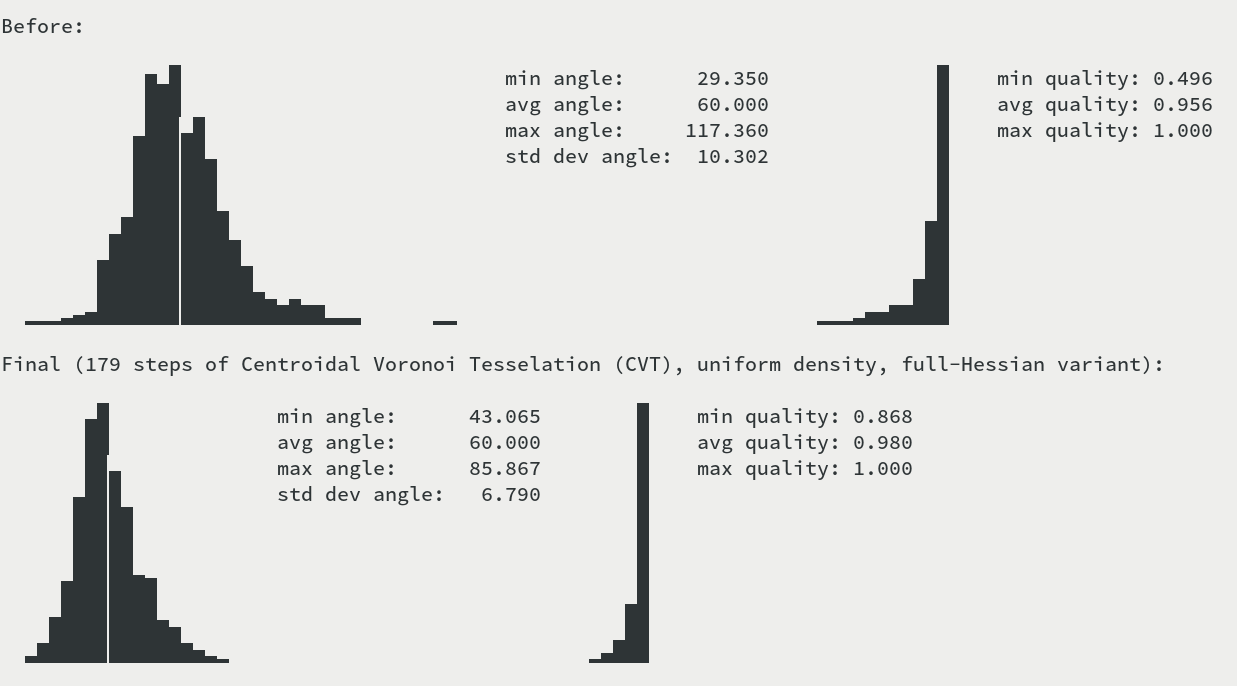
The left hand-side graph shows the distribution of angles (the grid line is at the
optimal 60 degrees). The right hand-side graph shows the distribution of simplex
quality, where quality is twice the ratio of circumcircle and incircle radius.
All command-line options are documented at
```
optimesh -h
```
### Showcase
The following examples show the various algorithms at work, all starting from the same
randomly generated disk mesh above. The cell coloring indicates quality; dark green is
bad, yellow is good.
#### CVT (centroidal Voronoi tessellation)
|  |  |  |
| :---------------------------------------------------------------------------------------------------------------------------: | :------------------------------------------------------------------------------------------------: | :------------------------------------------------------------------------------------------------: |
| uniform-density relaxed [Lloyd's algorithm](https://en.wikipedia.org/wiki/Lloyd%27s_algorithm) (`--method lloyd --omega 2.0`) | uniform-density quasi-Newton iteration (block-diagonal Hessian, `--method cvt-block-diagonal`) | uniform-density quasi-Newton iteration (default method, full Hessian, `--method cvt-full`) |
Centroidal Voronoi tessellation smoothing ([Du et al.](#relevant-publications)) is one
of the oldest and most reliable approaches. optimesh provides classical Lloyd smoothing
as well as several variants that result in better meshes.
#### CPT (centroidal patch tessellation)
|  |  |  |
| :-------------------------------------------------------------------------------------------------------------------------------------: | :----------------------------------------------------------------------------------------------: | :----------------------------------------------------------------------------------------------: |
| density-preserving linear solve ([Laplacian smoothing](https://en.wikipedia.org/wiki/Laplacian_smoothing), `--method cpt-linear-solve`) | uniform-density fixed-point iteration (`--method cpt-fixed-point`) | uniform-density quasi-Newton (`--method cpt-quasi-newton`) |
A smoothing method suggested by [Chen and Holst](#relevant-publications), mimicking CVT
but much more easily implemented. The density-preserving variant leads to the exact same
equation system as Laplacian smoothing, so CPT smoothing can be thought of as a
generalization.
The uniform-density variants are implemented classically as a fixed-point iteration and
as a quasi-Newton method. The latter typically converges faster.
#### ODT (optimal Delaunay tessellation)
|  |  |  |
| :------------------------------------------------------------------------------------: | :----------------------------------------------------------------------------------------------: | :--------------------------------------------------------------------------------------------------: |
| density-preserving fixed-point iteration (`--method odt-dp-fp`) | uniform-density fixed-point iteration (`--method odt-fixed-point`) | uniform-density BFGS (`--method odt-bfgs`) |
Optimal Delaunay Triangulation (ODT) as suggested by [Chen and
Holst](#relevant-publications). Typically superior to CPT, but also more expensive to
compute.
Implemented once classically as a fixed-point iteration, once as a nonlinear
optimization method. The latter typically leads to better results.
### Using optimesh from Python
You can also use optimesh in a Python program. Try
<!--pytest.mark.skip-->
```python
import optimesh
# [...] create points, cells [...]
points, cells = optimesh.optimize_points_cells(
points, cells, "CVT (block-diagonal)", 1.0e-5, 100
)
# or create a meshplex Mesh
import meshplex
mesh = meshplex.MeshTri(points, cells)
optimesh.optimize(mesh, "CVT (block-diagonal)", 1.0e-5, 100)
# mesh.points, mesh.cells, ...
```
If you only want to do one optimization step, do
<!--pytest.mark.skip-->
```python
points = optimesh.get_new_points(mesh, "CVT (block-diagonal)")
```
### Surface mesh smoothing
optimesh also supports optimization of triangular meshes on surfaces which are defined
implicitly by a level set function (e.g., spheres). You'll need to specify the function
and its gradient, so you'll have to do it in Python:
```python
import meshzoo
import optimesh
points, cells = meshzoo.tetra_sphere(20)
class Sphere:
def f(self, x):
return 1.0 - (x[0] ** 2 + x[1] ** 2 + x[2] ** 2)
def grad(self, x):
return -2 * x
# You can use all methods in optimesh:
points, cells = optimesh.optimize_points_cells(
points,
cells,
"CVT (full)",
1.0e-2,
100,
verbose=False,
implicit_surface=Sphere(),
# step_filename_format="out{:03d}.vtk"
)
```
This code first generates a mediocre mesh on a sphere using
[meshzoo](https://github.com/nschloe/meshzoo/),
<img src="https://raw.githubusercontent.com/meshpro/optimesh/assets/tetra-sphere.png" width="20%">
and then optimizes. Some results:
|  |  |  |
| :-------------------------------------------------------------------------------------: | :------------------------------------------------------------------------------------------: | :--------------------------------------------------------------------------------------------: |
| CPT | ODT | CVT (full Hessian) |
### Which method is best?
From practical experiments, it seems that the CVT smoothing variants, e.g.,
```
optimesh in.vtk out.vtk -m cvt-uniform-qnf
```
give very satisfactory results. (This is also the default method, so you don't need to
specify it explicitly.) Here is a comparison of all uniform-density methods applied to
the random circle mesh seen above:
<img src="https://raw.githubusercontent.com/meshpro/optimesh/assets/comparison.svg" width="90%">
(Mesh quality is twice the ratio of incircle and circumcircle radius, with the maximum
being 1.)
### Why optimize?
| <img src="https://raw.githubusercontent.com/meshpro/optimesh/assets/gmsh.png" width="80%"> | <img src="https://raw.githubusercontent.com/meshpro/optimesh/assets/gmsh-optimesh.png" width="80%"> | <img src="https://raw.githubusercontent.com/meshpro/optimesh/assets/dmsh.png" width="80%"> |
| :----------------------------------------------------------------------------------------: | :-------------------------------------------------------------------------------------------------: | :----------------------------------------------------------------------------------------: |
| Gmsh mesh | Gmsh mesh after optimesh | [dmsh](//github.com/nschloe/dmsh) mesh |
Let us compare the properties of the Poisson problem (_Δu = f_ with Dirichlet boundary
conditions) when solved on different meshes of the unit circle. The first mesh is the
on generated by [Gmsh](http://gmsh.info/), the second the same mesh but optimized with
optimesh, the third a very high-quality [dmsh](https://github.com/nschloe/dmsh) mesh.
We consider meshings of the circle with an increasing number of points:
|  |  |  |
| :-----------------------------------------------------------------------------------------: | :-----------------------------------------------------------------------------------: | :-------------------------------------------------------------------------------: |
| average cell quality | condition number of the Poisson matrix | number of CG steps for Poisson problem |
Quite clearly, the dmsh generator produces the highest-quality meshes (left).
The condition number of the corresponding Poisson matrices is lowest for the high
quality meshes (middle); one would hence suspect faster convergence with Krylov methods.
Indeed, most CG iterations are necessary on the Gmsh mesh (right). After optimesh, one saves
between 10 and 20 percent of iterations/computing time. The dmsh mesh cuts the number of
iterations in _half_.
### Access from Python
All optimesh functions can also be accessed from Python directly, for example:
<!--pytest.mark.skip-->
```python
import optimesh
X, cells = optimesh.odt.fixed_point(X, cells, 1.0e-2, 100, verbose=False)
```
### Relevant publications
- [Qiang Du, Vance Faber, and Max Gunzburger, _Centroidal Voronoi Tessellations: Applications and Algorithms_,
SIAM Rev., 41(4), 1999, 637–676.](https://doi.org/10.1137/S0036144599352836)
- [Yang Liu et al., _On centroidal Voronoi tessellation—Energy smoothness and fast computation_,
ACM Transactions on Graphics, Volume 28, Issue 4, August 2009.](https://dl.acm.org/doi/10.1145/1559755.1559758)
- [Long Chen, Michael Holst, _Efficient mesh optimization schemes based on Optimal Delaunay Triangulations_,
Comput. Methods Appl. Mech. Engrg. 200 (2011) 967–984.](https://doi.org/10.1016/j.cma.2010.11.007)
Raw data
{
"_id": null,
"home_page": null,
"name": "optimesh",
"maintainer": null,
"docs_url": null,
"requires_python": ">=3.8",
"maintainer_email": null,
"keywords": "engineering, mathematics, mesh, mesh generation, optimization, physics",
"author": null,
"author_email": "Nico Schl\u00f6mer <nico.schloemer@gmail.com>",
"download_url": null,
"platform": null,
"description": "<p align=\"center\">\n <a href=\"https://github.com/nschloe/optimesh\"><img alt=\"optimesh\" src=\"https://raw.githubusercontent.com/meshpro/optimesh/assets/optimesh-logo.svg\" width=\"60%\"></a>\n <p align=\"center\">Triangular mesh optimization.</p>\n</p>\n\n[](https://pypi.org/project/optimesh/)\n[](https://pypi.org/project/optimesh/)\n[](https://doi.org/10.5281/zenodo.4728056)\n[](https://github.com/nschloe/optimesh)\n[](https://pypistats.org/packages/optimesh)\n\n[](https://discord.gg/PBCCvwHqpv)\n\nSeveral mesh smoothing/optimization methods with one simple interface. optimesh\n\n- is fast,\n- preserves submeshes,\n- only works for triangular meshes, flat and on a surface, (for now; upvote [this\n issue](https://github.com/nschloe/optimesh/issues/17) if you're interested in\n tetrahedral mesh smoothing), and\n- supports all mesh formats that [meshio](https://github.com/nschloe/meshio) can\n handle.\n\n### Installation\n\nInstall optimesh [from PyPI](https://pypi.org/project/optimesh/) with\n\n```\npip install optimesh\n```\n\n### How to get a license\n\nLicenses for personal and academic use can be purchased\n[here](https://buy.stripe.com/5kA3eV8t8af83iE9AE).\nYou'll receive a confirmation email with a license key.\nInstall the key with\n\n```\nslim install <your-license-key>\n```\n\non your machine and you're good to go.\n\nFor commercial use, please contact support@mondaytech.com.\n\n### Using optimesh\n\nExample call:\n\n```\noptimesh in.e out.vtk\n```\n\nOutput:\n\n\nThe left hand-side graph shows the distribution of angles (the grid line is at the\noptimal 60 degrees). The right hand-side graph shows the distribution of simplex\nquality, where quality is twice the ratio of circumcircle and incircle radius.\n\nAll command-line options are documented at\n\n```\noptimesh -h\n```\n\n### Showcase\n\n\n\nThe following examples show the various algorithms at work, all starting from the same\nrandomly generated disk mesh above. The cell coloring indicates quality; dark green is\nbad, yellow is good.\n\n#### CVT (centroidal Voronoi tessellation)\n\n|  |  |  |\n| :---------------------------------------------------------------------------------------------------------------------------: | :------------------------------------------------------------------------------------------------: | :------------------------------------------------------------------------------------------------: |\n| uniform-density relaxed [Lloyd's algorithm](https://en.wikipedia.org/wiki/Lloyd%27s_algorithm) (`--method lloyd --omega 2.0`) | uniform-density quasi-Newton iteration (block-diagonal Hessian, `--method cvt-block-diagonal`) | uniform-density quasi-Newton iteration (default method, full Hessian, `--method cvt-full`) |\n\nCentroidal Voronoi tessellation smoothing ([Du et al.](#relevant-publications)) is one\nof the oldest and most reliable approaches. optimesh provides classical Lloyd smoothing\nas well as several variants that result in better meshes.\n\n#### CPT (centroidal patch tessellation)\n\n|  |  |  |\n| :-------------------------------------------------------------------------------------------------------------------------------------: | :----------------------------------------------------------------------------------------------: | :----------------------------------------------------------------------------------------------: |\n| density-preserving linear solve ([Laplacian smoothing](https://en.wikipedia.org/wiki/Laplacian_smoothing), `--method cpt-linear-solve`) | uniform-density fixed-point iteration (`--method cpt-fixed-point`) | uniform-density quasi-Newton (`--method cpt-quasi-newton`) |\n\nA smoothing method suggested by [Chen and Holst](#relevant-publications), mimicking CVT\nbut much more easily implemented. The density-preserving variant leads to the exact same\nequation system as Laplacian smoothing, so CPT smoothing can be thought of as a\ngeneralization.\n\nThe uniform-density variants are implemented classically as a fixed-point iteration and\nas a quasi-Newton method. The latter typically converges faster.\n\n#### ODT (optimal Delaunay tessellation)\n\n|  |  |  |\n| :------------------------------------------------------------------------------------: | :----------------------------------------------------------------------------------------------: | :--------------------------------------------------------------------------------------------------: |\n| density-preserving fixed-point iteration (`--method odt-dp-fp`) | uniform-density fixed-point iteration (`--method odt-fixed-point`) | uniform-density BFGS (`--method odt-bfgs`) |\n\nOptimal Delaunay Triangulation (ODT) as suggested by [Chen and\nHolst](#relevant-publications). Typically superior to CPT, but also more expensive to\ncompute.\n\nImplemented once classically as a fixed-point iteration, once as a nonlinear\noptimization method. The latter typically leads to better results.\n\n### Using optimesh from Python\n\nYou can also use optimesh in a Python program. Try\n\n<!--pytest.mark.skip-->\n\n```python\nimport optimesh\n\n# [...] create points, cells [...]\n\npoints, cells = optimesh.optimize_points_cells(\n points, cells, \"CVT (block-diagonal)\", 1.0e-5, 100\n)\n\n# or create a meshplex Mesh\nimport meshplex\n\nmesh = meshplex.MeshTri(points, cells)\noptimesh.optimize(mesh, \"CVT (block-diagonal)\", 1.0e-5, 100)\n# mesh.points, mesh.cells, ...\n```\n\nIf you only want to do one optimization step, do\n\n<!--pytest.mark.skip-->\n\n```python\npoints = optimesh.get_new_points(mesh, \"CVT (block-diagonal)\")\n```\n\n### Surface mesh smoothing\n\noptimesh also supports optimization of triangular meshes on surfaces which are defined\nimplicitly by a level set function (e.g., spheres). You'll need to specify the function\nand its gradient, so you'll have to do it in Python:\n\n```python\nimport meshzoo\nimport optimesh\n\npoints, cells = meshzoo.tetra_sphere(20)\n\n\nclass Sphere:\n def f(self, x):\n return 1.0 - (x[0] ** 2 + x[1] ** 2 + x[2] ** 2)\n\n def grad(self, x):\n return -2 * x\n\n\n# You can use all methods in optimesh:\npoints, cells = optimesh.optimize_points_cells(\n points,\n cells,\n \"CVT (full)\",\n 1.0e-2,\n 100,\n verbose=False,\n implicit_surface=Sphere(),\n # step_filename_format=\"out{:03d}.vtk\"\n)\n```\n\nThis code first generates a mediocre mesh on a sphere using\n[meshzoo](https://github.com/nschloe/meshzoo/),\n\n<img src=\"https://raw.githubusercontent.com/meshpro/optimesh/assets/tetra-sphere.png\" width=\"20%\">\n\nand then optimizes. Some results:\n\n|  |  |  |\n| :-------------------------------------------------------------------------------------: | :------------------------------------------------------------------------------------------: | :--------------------------------------------------------------------------------------------: |\n| CPT | ODT | CVT (full Hessian) |\n\n### Which method is best?\n\nFrom practical experiments, it seems that the CVT smoothing variants, e.g.,\n\n```\noptimesh in.vtk out.vtk -m cvt-uniform-qnf\n```\n\ngive very satisfactory results. (This is also the default method, so you don't need to\nspecify it explicitly.) Here is a comparison of all uniform-density methods applied to\nthe random circle mesh seen above:\n\n<img src=\"https://raw.githubusercontent.com/meshpro/optimesh/assets/comparison.svg\" width=\"90%\">\n\n(Mesh quality is twice the ratio of incircle and circumcircle radius, with the maximum\nbeing 1.)\n\n### Why optimize?\n\n| <img src=\"https://raw.githubusercontent.com/meshpro/optimesh/assets/gmsh.png\" width=\"80%\"> | <img src=\"https://raw.githubusercontent.com/meshpro/optimesh/assets/gmsh-optimesh.png\" width=\"80%\"> | <img src=\"https://raw.githubusercontent.com/meshpro/optimesh/assets/dmsh.png\" width=\"80%\"> |\n| :----------------------------------------------------------------------------------------: | :-------------------------------------------------------------------------------------------------: | :----------------------------------------------------------------------------------------: |\n| Gmsh mesh | Gmsh mesh after optimesh | [dmsh](//github.com/nschloe/dmsh) mesh |\n\nLet us compare the properties of the Poisson problem (_\u0394u = f_ with Dirichlet boundary\nconditions) when solved on different meshes of the unit circle. The first mesh is the\non generated by [Gmsh](http://gmsh.info/), the second the same mesh but optimized with\noptimesh, the third a very high-quality [dmsh](https://github.com/nschloe/dmsh) mesh.\n\nWe consider meshings of the circle with an increasing number of points:\n\n|  |  |  |\n| :-----------------------------------------------------------------------------------------: | :-----------------------------------------------------------------------------------: | :-------------------------------------------------------------------------------: |\n| average cell quality | condition number of the Poisson matrix | number of CG steps for Poisson problem |\n\nQuite clearly, the dmsh generator produces the highest-quality meshes (left).\nThe condition number of the corresponding Poisson matrices is lowest for the high\nquality meshes (middle); one would hence suspect faster convergence with Krylov methods.\nIndeed, most CG iterations are necessary on the Gmsh mesh (right). After optimesh, one saves\nbetween 10 and 20 percent of iterations/computing time. The dmsh mesh cuts the number of\niterations in _half_.\n\n### Access from Python\n\nAll optimesh functions can also be accessed from Python directly, for example:\n\n<!--pytest.mark.skip-->\n\n```python\nimport optimesh\n\nX, cells = optimesh.odt.fixed_point(X, cells, 1.0e-2, 100, verbose=False)\n```\n\n### Relevant publications\n\n- [Qiang Du, Vance Faber, and Max Gunzburger, _Centroidal Voronoi Tessellations: Applications and Algorithms_,\n SIAM Rev., 41(4), 1999, 637\u2013676.](https://doi.org/10.1137/S0036144599352836)\n\n- [Yang Liu et al., _On centroidal Voronoi tessellation\u2014Energy smoothness and fast computation_,\n ACM Transactions on Graphics, Volume 28, Issue 4, August 2009.](https://dl.acm.org/doi/10.1145/1559755.1559758)\n\n- [Long Chen, Michael Holst, _Efficient mesh optimization schemes based on Optimal Delaunay Triangulations_,\n Comput. Methods Appl. Mech. Engrg. 200 (2011) 967\u2013984.](https://doi.org/10.1016/j.cma.2010.11.007)\n",
"bugtrack_url": null,
"license": null,
"summary": "Mesh optimization/smoothing",
"version": "0.10.4",
"project_urls": {
"Homepage": "https://github.com/meshpro/optimesh",
"Issues": "https://github.com/meshpro/optimesh/issues"
},
"split_keywords": [
"engineering",
" mathematics",
" mesh",
" mesh generation",
" optimization",
" physics"
],
"urls": [
{
"comment_text": "",
"digests": {
"blake2b_256": "ce58ce9b5100082ac7ec5baf10bf5256bab221a5553c46f5b27a155b590c2bf1",
"md5": "4d75fb9d9f007fe7fc38d54b9f5b629b",
"sha256": "86b05e4f4cc6e2ba1d4114c5b0d5a146898c5e1cf942d87c63e75a21ec1d6759"
},
"downloads": -1,
"filename": "optimesh-0.10.4-py3-none-any.whl",
"has_sig": false,
"md5_digest": "4d75fb9d9f007fe7fc38d54b9f5b629b",
"packagetype": "bdist_wheel",
"python_version": "py3",
"requires_python": ">=3.8",
"size": 41733,
"upload_time": "2024-06-14T09:27:42",
"upload_time_iso_8601": "2024-06-14T09:27:42.990913Z",
"url": "https://files.pythonhosted.org/packages/ce/58/ce9b5100082ac7ec5baf10bf5256bab221a5553c46f5b27a155b590c2bf1/optimesh-0.10.4-py3-none-any.whl",
"yanked": false,
"yanked_reason": null
}
],
"upload_time": "2024-06-14 09:27:42",
"github": true,
"gitlab": false,
"bitbucket": false,
"codeberg": false,
"github_user": "meshpro",
"github_project": "optimesh",
"travis_ci": false,
"coveralls": false,
"github_actions": false,
"lcname": "optimesh"
}
JSON
