| Name | reyna JSON |
| Version |
1.3.0
 JSON
JSON |
| download |
| home_page | None |
| Summary | A minimal overhead, vectorised, polygonal discontinuous Galerkin finite element library. |
| upload_time | 2025-08-27 23:51:13 |
| maintainer | None |
| docs_url | None |
| author | None |
| requires_python | >=3.8 |
| license | MIT License
Copyright (c) 2025 Matthew Evans
Permission is hereby granted, free of charge, to any person obtaining a copy
of this software and associated documentation files (the "Software"), to deal
in the Software without restriction, including without limitation the rights
to use, copy, modify, merge, publish, distribute, sublicense, and/or sell
copies of the Software, and to permit persons to whom the Software is
furnished to do so, subject to the following conditions:
The above copyright notice and this permission notice shall be included in all
copies or substantial portions of the Software.
THE SOFTWARE IS PROVIDED "AS IS", WITHOUT WARRANTY OF ANY KIND, EXPRESS OR
IMPLIED, INCLUDING BUT NOT LIMITED TO THE WARRANTIES OF MERCHANTABILITY,
FITNESS FOR A PARTICULAR PURPOSE AND NONINFRINGEMENT. IN NO EVENT SHALL THE
AUTHORS OR COPYRIGHT HOLDERS BE LIABLE FOR ANY CLAIM, DAMAGES OR OTHER
LIABILITY, WHETHER IN AN ACTION OF CONTRACT, TORT OR OTHERWISE, ARISING FROM,
OUT OF OR IN CONNECTION WITH THE SOFTWARE OR THE USE OR OTHER DEALINGS IN THE
SOFTWARE. |
| keywords |
discontinuous
galerkin
finite
element
numerics
methods
numerical analysis
dicontinuous galerkin
dg
finite element methods
na
pdes
partial
differential
equations
partial differential equations
linear algebra
la
sparse
matrices
|
| VCS |
|
| bugtrack_url |
|
| requirements |
No requirements were recorded.
|
| Travis-CI |
No Travis.
|
| coveralls test coverage |
No coveralls.
|
# reyna
A lightweight Python package for solving partial differential equations (PDEs) using polygonal discontinuous
Galerkin finite elements, providing a flexible and efficient way to approximate solutions to complex PDEs.
### Features
- Support for various polygonal element types (e.g., triangles, quadrilaterals, etc.)
- Easy-to-use API for mesh generation, assembly, and solving PDEs.
- High performance with optimized solvers for large-scale problems.
- Supports both linear and nonlinear equations.
- Extensible framework: easily integrate custom element types, solvers, or boundary conditions.
### Installation
You can install the package via pip. First, clone the repository and then install it using pip:
Install from PyPI:
```shell
pip install reyna
```
Install from source:
```shell
pip install git+https://github.com/mattevs24/reyna.git
```
## Example Usage
### Create a Simple Mesh
A simple example to begin with is the `RectangleDomain` object. This requires just the bounding
box as an input. In this case, we consider the unit square; $[0, 1]^2$. We then use `poly_mesher`
to generate a bounded Voronoi mesh of the domain. This uses Lloyd's algorithm, which can produce
edges that are machine precision in length. To avoid this for benchmarking and other critical
purposes, use the `cleaned` keyword, set to `True`.
```python
import numpy as np
from reyna.polymesher.two_dimensional.domains import RectangleDomain
from reyna.polymesher.two_dimensional.main import poly_mesher
domain = RectangleDomain(bounding_box=np.array([[0, 1], [0, 1]]))
poly_mesh = poly_mesher(domain, max_iterations=10, n_points=1024)
```
### Generating the Geometry Information
The DGFEM code requires additional information about the mesh to be able to run, including which edges
are boundary edges and their corresponding normals as well as information on a given subtriagulation to
be able to numerically integrate with the required precision. This is done using the `DGFEMgeometry` function.
```python
from reyna.geometry.two_dimensional.DGFEM import DGFEMGeometry
geometry = DGFEMGeometry(poly_mesh)
```
### Defining the Partial Differential Equation
To define the PDE, we need to call the DGFEM object. We then add data in the form of the general
coefficients for a (up-to) second order PDE of the form
$$
-\nabla\cdot(a\nabla u) + b\cdot\nabla u + cu = f
$$
where $a$ is the diffusion tensor, $b$ is the advection vector, $c$ is the reation functional and
$f$ is the forcing functional. All of these functions must be able to take in a (N, 2) array of
points and output tensors of the correct shape; (N, 2, 2), (N, 2), (N,) and (N,) respectively. An
example is given
```python
def diffusion(x):
out = np.zeros((x.shape[0], 2, 2), dtype=np.float64)
for i in range(x.shape[0]):
out[i, 0, 0] = 1.0
out[i, 1, 1] = 1.0
return out
advection = lambda x: np.ones(x.shape, dtype=float)
reaction = lambda x: np.pi ** 2 * np.ones(x.shape[0], dtype=float)
forcing = lambda x: np.pi * (np.cos(np.pi * x[:, 0]) * np.sin(np.pi * x[:, 1]) +
np.sin(np.pi * x[:, 0]) * np.cos(np.pi * x[:, 1])) + \
3.0 * np.pi ** 2 * np.sin(np.pi * x[:, 0]) * np.sin(np.pi * x[:, 1])
solution = lambda x: np.sin(np.pi * x[:, 0]) * np.sin(np.pi * x[:, 1])
```
We use the solution function here as the boundary conditions for the solver.
### Adding data and Assembly
We can now call the solver, add the data and assemble.
```python
from reyna.DGFEM.two_dimensional.main import DGFEM
dg = DGFEM(geometry, polynomial_degree=1)
dg.add_data(
diffusion=diffusion,
advection=advection,
reaction=reaction,
dirichlet_bcs=solution,
forcing=forcing
)
dg.dgfem(solve=True)
```
Setting the `solve` input to `True` generates the solution vector. If this is `False`, just the
stiffness matrix and data vector are generated.
### Visualize the solution
We also have a method to plot the data, `plot_DG`, but this is limited to polynomial degree 1
with limited support for polynomial degree 0. See the example below
```python
dg.plot_DG()
```
or for more customisation, use the function `plot_DG`,
```python
from reyna.DGFEM.two_dimensional.plotter import plot_DG
plot_DG(dg.solution, geometry, dg.polydegree)
```
For the given example, we have the solution plot
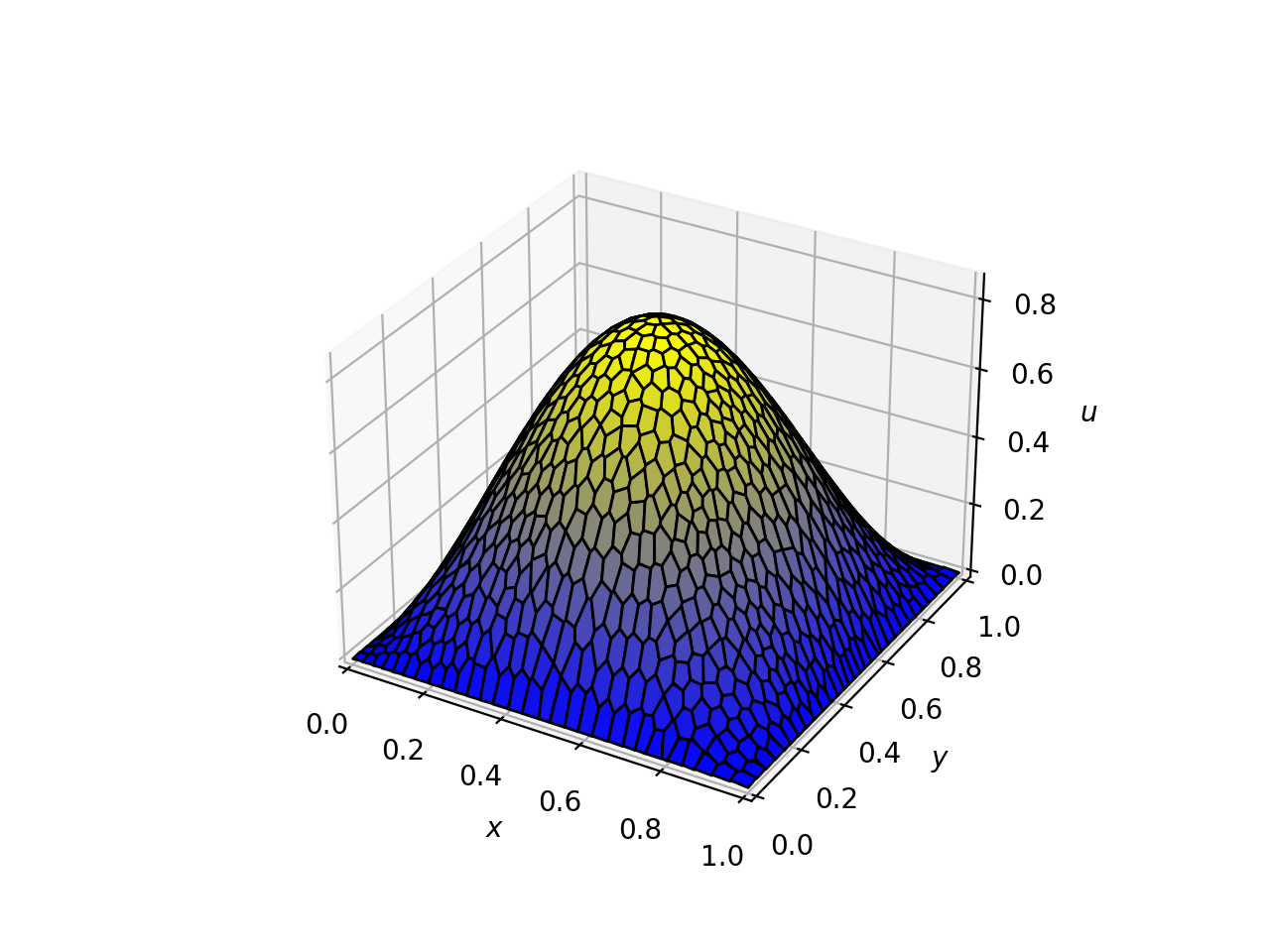
### Benchmarking
We have a benchmarking file that may be run availible in the main DGFEM directory. But we also provide
an example of the code to be able to calculate yourself
```python
def grad_solution(x: np.ndarray):
u_x = np.pi * np.cos(np.pi * x[:, 0]) * np.sin(np.pi * x[:, 1])
u_y = np.pi * np.sin(np.pi * x[:, 0]) * np.cos(np.pi * x[:, 1])
return np.vstack((u_x, u_y)).T
dg_error, l2_error, h1_error = dg.errors(
exact_solution=solution,
div_advection=lambda x: np.zeros(x.shape[0]),
grad_exact_solution=grad_solution
)
```
Often, the error rate is calcuated against the maximal cell diameter; the code for this is included in
the `DGFEM` class under the `h` method as well as the `DGFEMgeometry` class under the `h` method (`DGFEMgeometry`
additionally contains all the local values of `h` across the mesh).
```python
h = dg.h
h = geometry.h
```
Note that in a purely advection/diffusion problem, some of the norms are unavailable and return
a `None` value.
## A more advanced Domain Example
There are many predefined domains in the `reyna/polymesher/two_dimensional/domains` folder including this
more advanced `CircleCircleDomain()` domain;

## Example Notebooks
There are Jupyter notebooks availible in the GitHub repository which run through several examples of this
package in action. This also runs through examples of benchmarking and custom domain generation.
## Documentation
For detailed usage and API documentation, please visit our (soon to be) readthedocs.
The above example and notebooks cover most cases and the current docstrings are very thorough.
## Contributing
This project accepts contributions - see the CONTRIBUTING.md file for details.
## License
This project is licensed under the MIT License - see the LICENSE.md file for details.
## Credits & Acknowledgements
This package was developed by mattevs24 during a PhD programme funded by the French Alternative Energies
and Atomic Energy Commission. A Special thanks to the support of Ansar Calloo, Fraçois Madiot throughout
the PhD so far. A further thank you to my interal supervisors Tristan Pryer and Luca Zanetti for their role
in this project too and useful feedback on usability and support. Finally, a thank you to my partner
Reyna who puts up with all this nonsense!
## Upcoming Updates
There are many features that remain to add to this code! We hope to add support for the following features
- Mixed-type problems: support for multiple types of PDE on the same domain.
- Full readthedocs documentation to support the further developement and use of this package.
Raw data
{
"_id": null,
"home_page": null,
"name": "reyna",
"maintainer": null,
"docs_url": null,
"requires_python": ">=3.8",
"maintainer_email": null,
"keywords": "discontinuous, Galerkin, finite, element, numerics, methods, numerical analysis, dicontinuous Galerkin, dG, finite element methods, NA, pdes, partial, differential, equations, partial differential equations, linear algebra, LA, sparse, matrices",
"author": null,
"author_email": "mattevs24 <matt.evans2411@gmail.com>",
"download_url": "https://files.pythonhosted.org/packages/07/bd/cb5c3856a30ec1dca5e354f068d4c6dd1811c2870399d3b781555a0f7a13/reyna-1.3.0.tar.gz",
"platform": null,
"description": "# reyna\n\nA lightweight Python package for solving partial differential equations (PDEs) using polygonal discontinuous \nGalerkin finite elements, providing a flexible and efficient way to approximate solutions to complex PDEs.\n\n### Features\n\n- Support for various polygonal element types (e.g., triangles, quadrilaterals, etc.)\n- Easy-to-use API for mesh generation, assembly, and solving PDEs.\n- High performance with optimized solvers for large-scale problems.\n- Supports both linear and nonlinear equations.\n- Extensible framework: easily integrate custom element types, solvers, or boundary conditions.\n\n### Installation\n\nYou can install the package via pip. First, clone the repository and then install it using pip:\n\nInstall from PyPI:\n\n```shell\npip install reyna\n```\n\nInstall from source:\n\n```shell\npip install git+https://github.com/mattevs24/reyna.git\n```\n\n## Example Usage\n\n### Create a Simple Mesh\n\nA simple example to begin with is the `RectangleDomain` object. This requires just the bounding\nbox as an input. In this case, we consider the unit square; $[0, 1]^2$. We then use `poly_mesher` \nto generate a bounded Voronoi mesh of the domain. This uses Lloyd's algorithm, which can produce\nedges that are machine precision in length. To avoid this for benchmarking and other critical \npurposes, use the `cleaned` keyword, set to `True`.\n\n```python\nimport numpy as np\n\nfrom reyna.polymesher.two_dimensional.domains import RectangleDomain\nfrom reyna.polymesher.two_dimensional.main import poly_mesher\n\ndomain = RectangleDomain(bounding_box=np.array([[0, 1], [0, 1]]))\npoly_mesh = poly_mesher(domain, max_iterations=10, n_points=1024)\n```\n\n### Generating the Geometry Information\n\nThe DGFEM code requires additional information about the mesh to be able to run, including which edges\nare boundary edges and their corresponding normals as well as information on a given subtriagulation to \nbe able to numerically integrate with the required precision. This is done using the `DGFEMgeometry` function.\n\n```python\nfrom reyna.geometry.two_dimensional.DGFEM import DGFEMGeometry\n\ngeometry = DGFEMGeometry(poly_mesh)\n```\n\n### Defining the Partial Differential Equation\n\nTo define the PDE, we need to call the DGFEM object. We then add data in the form of the general\ncoefficients for a (up-to) second order PDE of the form\n\n$$\n-\\nabla\\cdot(a\\nabla u) + b\\cdot\\nabla u + cu = f\n$$\n\nwhere $a$ is the diffusion tensor, $b$ is the advection vector, $c$ is the reation functional and\n$f$ is the forcing functional. All of these functions must be able to take in a (N, 2) array of \npoints and output tensors of the correct shape; (N, 2, 2), (N, 2), (N,) and (N,) respectively. An \nexample is given\n\n```python\ndef diffusion(x):\n out = np.zeros((x.shape[0], 2, 2), dtype=np.float64)\n for i in range(x.shape[0]):\n out[i, 0, 0] = 1.0\n out[i, 1, 1] = 1.0\n return out\n\nadvection = lambda x: np.ones(x.shape, dtype=float)\nreaction = lambda x: np.pi ** 2 * np.ones(x.shape[0], dtype=float)\nforcing = lambda x: np.pi * (np.cos(np.pi * x[:, 0]) * np.sin(np.pi * x[:, 1]) +\n np.sin(np.pi * x[:, 0]) * np.cos(np.pi * x[:, 1])) + \\\n 3.0 * np.pi ** 2 * np.sin(np.pi * x[:, 0]) * np.sin(np.pi * x[:, 1])\n\nsolution = lambda x: np.sin(np.pi * x[:, 0]) * np.sin(np.pi * x[:, 1])\n```\n\nWe use the solution function here as the boundary conditions for the solver.\n\n### Adding data and Assembly\n\nWe can now call the solver, add the data and assemble.\n\n```python\n\nfrom reyna.DGFEM.two_dimensional.main import DGFEM\n\ndg = DGFEM(geometry, polynomial_degree=1)\n\ndg.add_data(\n diffusion=diffusion,\n advection=advection,\n reaction=reaction,\n dirichlet_bcs=solution,\n forcing=forcing\n )\n\ndg.dgfem(solve=True)\n```\n\nSetting the `solve` input to `True` generates the solution vector. If this is `False`, just the\nstiffness matrix and data vector are generated.\n\n### Visualize the solution\n\nWe also have a method to plot the data, `plot_DG`, but this is limited to polynomial degree 1\nwith limited support for polynomial degree 0. See the example below\n\n```python\ndg.plot_DG()\n```\n\nor for more customisation, use the function `plot_DG`,\n\n```python\nfrom reyna.DGFEM.two_dimensional.plotter import plot_DG\n\nplot_DG(dg.solution, geometry, dg.polydegree)\n```\n\nFor the given example, we have the solution plot\n\n\n\n### Benchmarking\n\nWe have a benchmarking file that may be run availible in the main DGFEM directory. But we also provide\nan example of the code to be able to calculate yourself\n\n```python\n\ndef grad_solution(x: np.ndarray):\n u_x = np.pi * np.cos(np.pi * x[:, 0]) * np.sin(np.pi * x[:, 1])\n u_y = np.pi * np.sin(np.pi * x[:, 0]) * np.cos(np.pi * x[:, 1])\n\n return np.vstack((u_x, u_y)).T\n\ndg_error, l2_error, h1_error = dg.errors(\n exact_solution=solution,\n div_advection=lambda x: np.zeros(x.shape[0]),\n grad_exact_solution=grad_solution\n)\n```\n\nOften, the error rate is calcuated against the maximal cell diameter; the code for this is included in\nthe `DGFEM` class under the `h` method as well as the `DGFEMgeometry` class under the `h` method (`DGFEMgeometry` \nadditionally contains all the local values of `h` across the mesh).\n\n```python\nh = dg.h\nh = geometry.h\n```\n\nNote that in a purely advection/diffusion problem, some of the norms are unavailable and return\na `None` value.\n\n## A more advanced Domain Example\n\nThere are many predefined domains in the `reyna/polymesher/two_dimensional/domains` folder including this\nmore advanced `CircleCircleDomain()` domain;\n\n\n\n## Example Notebooks\n\nThere are Jupyter notebooks availible in the GitHub repository which run through several examples of this\npackage in action. This also runs through examples of benchmarking and custom domain generation.\n\n## Documentation\n\nFor detailed usage and API documentation, please visit our (soon to be) readthedocs. \nThe above example and notebooks cover most cases and the current docstrings are very thorough.\n\n## Contributing\n\nThis project accepts contributions - see the CONTRIBUTING.md file for details.\n\n## License\n\nThis project is licensed under the MIT License - see the LICENSE.md file for details.\n\n## Credits & Acknowledgements\n\nThis package was developed by mattevs24 during a PhD programme funded by the French Alternative Energies \nand Atomic Energy Commission. A Special thanks to the support of Ansar Calloo, Fra\u00e7ois Madiot throughout\nthe PhD so far. A further thank you to my interal supervisors Tristan Pryer and Luca Zanetti for their role\nin this project too and useful feedback on usability and support. Finally, a thank you to my partner\nReyna who puts up with all this nonsense!\n\n## Upcoming Updates\n\nThere are many features that remain to add to this code! We hope to add support for the following features\n\n- Mixed-type problems: support for multiple types of PDE on the same domain.\n- Full readthedocs documentation to support the further developement and use of this package.\n",
"bugtrack_url": null,
"license": "MIT License\n \n Copyright (c) 2025 Matthew Evans\n \n Permission is hereby granted, free of charge, to any person obtaining a copy\n of this software and associated documentation files (the \"Software\"), to deal\n in the Software without restriction, including without limitation the rights\n to use, copy, modify, merge, publish, distribute, sublicense, and/or sell\n copies of the Software, and to permit persons to whom the Software is\n furnished to do so, subject to the following conditions:\n \n The above copyright notice and this permission notice shall be included in all\n copies or substantial portions of the Software.\n \n THE SOFTWARE IS PROVIDED \"AS IS\", WITHOUT WARRANTY OF ANY KIND, EXPRESS OR\n IMPLIED, INCLUDING BUT NOT LIMITED TO THE WARRANTIES OF MERCHANTABILITY,\n FITNESS FOR A PARTICULAR PURPOSE AND NONINFRINGEMENT. IN NO EVENT SHALL THE\n AUTHORS OR COPYRIGHT HOLDERS BE LIABLE FOR ANY CLAIM, DAMAGES OR OTHER\n LIABILITY, WHETHER IN AN ACTION OF CONTRACT, TORT OR OTHERWISE, ARISING FROM,\n OUT OF OR IN CONNECTION WITH THE SOFTWARE OR THE USE OR OTHER DEALINGS IN THE\n SOFTWARE.",
"summary": "A minimal overhead, vectorised, polygonal discontinuous Galerkin finite element library.",
"version": "1.3.0",
"project_urls": null,
"split_keywords": [
"discontinuous",
" galerkin",
" finite",
" element",
" numerics",
" methods",
" numerical analysis",
" dicontinuous galerkin",
" dg",
" finite element methods",
" na",
" pdes",
" partial",
" differential",
" equations",
" partial differential equations",
" linear algebra",
" la",
" sparse",
" matrices"
],
"urls": [
{
"comment_text": null,
"digests": {
"blake2b_256": "eff16855041b11cb1d8f222c3bd5f502a390800a370663a78447e891d686e9f4",
"md5": "27598445bf5f669695224c83ba9c1831",
"sha256": "9addd894b5f7abc93a6f9168ddf9e220e81d22591bf3add6788e4633ae72ecee"
},
"downloads": -1,
"filename": "reyna-1.3.0-py3-none-any.whl",
"has_sig": false,
"md5_digest": "27598445bf5f669695224c83ba9c1831",
"packagetype": "bdist_wheel",
"python_version": "py3",
"requires_python": ">=3.8",
"size": 40223,
"upload_time": "2025-08-27T23:51:12",
"upload_time_iso_8601": "2025-08-27T23:51:12.452282Z",
"url": "https://files.pythonhosted.org/packages/ef/f1/6855041b11cb1d8f222c3bd5f502a390800a370663a78447e891d686e9f4/reyna-1.3.0-py3-none-any.whl",
"yanked": false,
"yanked_reason": null
},
{
"comment_text": null,
"digests": {
"blake2b_256": "07bdcb5c3856a30ec1dca5e354f068d4c6dd1811c2870399d3b781555a0f7a13",
"md5": "f0098d9e83055ddf2c88e5dcb53a4405",
"sha256": "6b961425c2d6c576d0ceaae74056b18cc257252565d3989836c889f8d52ea6f3"
},
"downloads": -1,
"filename": "reyna-1.3.0.tar.gz",
"has_sig": false,
"md5_digest": "f0098d9e83055ddf2c88e5dcb53a4405",
"packagetype": "sdist",
"python_version": "source",
"requires_python": ">=3.8",
"size": 35516,
"upload_time": "2025-08-27T23:51:13",
"upload_time_iso_8601": "2025-08-27T23:51:13.789069Z",
"url": "https://files.pythonhosted.org/packages/07/bd/cb5c3856a30ec1dca5e354f068d4c6dd1811c2870399d3b781555a0f7a13/reyna-1.3.0.tar.gz",
"yanked": false,
"yanked_reason": null
}
],
"upload_time": "2025-08-27 23:51:13",
"github": false,
"gitlab": false,
"bitbucket": false,
"codeberg": false,
"lcname": "reyna"
}