# sudoku - Python sudoku solver
This package contains utilities for solving [sudoku](https://en.wikipedia.org/wiki/Sudoku) puzzles
using a variety of different algorithms.
## Installation
The easiest way to install the package is to download it from [PyPI](https://pypi.org) using `pip`.
Note that `sudoku` depends on [Python](https://www.python.org/downloads/) 3.7 or newer; please
ensure that you have a semi-recent version of Python installed before proceeding.
Run the following command in a shell (a UNIX-like environment is assumed):
```
$ pip install sudoku-ui
```
The package does not have any dependencies besides Python itself. If you wish to sandbox your
installation inside a virtual environment, you may choose to use
[virtualenvwrapper](https://virtualenvwrapper.readthedocs.io/en/latest/) or a similar
utility to do so.
When successfully installed, a program called `sudoku` will be placed on your `PATH`. See the
Usage section below for details about how to use this program.
## Usage
At any time, you can use the `-h` or `--help` flags to see a summary of options that the program accepts.
```
$ sudoku -h
usage: sudoku [-h] [-s SUDOKU] [-n NAME] [-a {brute-force,constraint,dlx}] [-g] [-d DELAY] [-q]
Solve sudoku puzzles.
optional arguments:
-h, --help show this help message and exit
-s SUDOKU, --sudoku SUDOKU, --string SUDOKU, --sudoku-string SUDOKU
A string representing a sudoku puzzle to solve
-n NAME, --name NAME The name of a sample puzzle to solve (for demo purposes)
-a {brute-force,constraint,dlx}, --algorithm {brute-force,constraint,dlx}
The algorithm to use to solve the puzzle
-g, --gui, --ui Display a GUI showing the puzzle being solved (not available for DLX mode)
-d DELAY, --delay DELAY, --delay-millis DELAY
How long to delay between steps in solving the puzzle (only applies in GUI mode)
-q, --quiet Reduce output verbosity (may be used multiple times)
```
The most basic usage is `sudoku -s <string>`, where `<string>` is a string representing a sudoku
puzzle to solve. The string should contain the value for each cell in the puzzle as a digit, or
a `0` or `.` for cells that are empty. Any other characters in the string will be ignored. For
example, the following three strings all represent the same puzzle to the program:
```
4.....8.5.3..........7......2.....6.....8.4......1.......6.3.7.5..2.....1.4......
```
```
400000805
030000000
000700000
020000060
000080400
000010000
000603070
500200000
104000000
```
```
4 . . |. . . |8 . 5
. 3 . |. . . |. . .
. . . |7 . . |. . .
------+------+------
. 2 . |. . . |. 6 .
. . . |. 8 . |4 . .
. . . |. 1 . |. . .
------+------+------
. . . |6 . 3 |. 7 .
5 . . |2 . . |. . .
1 . 4 |. . . |. . .
```
### Algorithms
By default, `sudoku` will use its fastest algorithm to solve the puzzle. This is a
**constraint-based** algorithm which uses the rules of sudoku to quickly deduce the solution
to any input puzzle (assuming the puzzle has enough clues to be solved). The constraint-based
algorithm typically solves a sudoku in about 0.1 seconds (tested on a mid-2015 MacBook Pro).
The implementation of the constraint-based solution algorithm is based heavily on the [prior work
of Peter Norvig](http://norvig.com/sudoku.html).
To specify a different algorithm, use the `-a` or `--algorithm` flags to `sudoku`. The other
available algorithms are `brute-force` and `dlx`. A description of each of these algorithms follows.
The **brute-force** algorithm tries all possible values for all empty cells in the puzzle, and
therefore its running time is exponential in the number of empty cells, i.e., *O(9^n)* where
*n* is the number of empty cells. Given a sudoku puzzle designed specifically to thwart the brute-force
strategy, this algorithm could take longer than the lifetime of the universe to find the solution!
In practice, however, this algorithm typically takes about 10 minutes to solve even a fairly hard sudoku.
The **DLX** algorithm uses the ["dancing links" algorithm](https://arxiv.org/pdf/cs/0011047.pdf) (due to
Don Knuth) to solve a sudoku puzzle by mapping it onto an equivalent [exact cover](https://en.wikipedia.org/wiki/Exact_cover)
problem and using a Python implementation of dancing links to solve the exact cover problem. This
algorithm by far the slowest of the three, often taking over a day to solve a typical input puzzle.
Profiling is needed to figure out where this algorithm is spending all of its time, since in theory this
strategy should be at least as efficient (if not more efficient) than the brute-force approach.
A re-implementation of the DLX algorithm in [Go](https://golang.org) may be developed at some point
in order to compare its performance against the (slow) Python implementation found here.
### Sample Puzzles
The `sudoku.sample_puzzles` module provides some sample sudoku puzzles for purposes of demoing or
testing the sudoku solver. The following puzzles are available:
* **empty-*n*** (1 ≤ *n* ≤ 64) - a sudoku puzzle with *n* empty cells (the remaining cells are already solved
with the correct values); these are useful for functional and performance testing of the slower algorithms
* **hard-*n*** (1 ≤ *n* ≤ 95) - a hard sudoku puzzle with only the initial clue cells already solved
Instead of providing a sudoku string to solve when running the `sudoku` program, you may instead provide the name
of a sample puzzle to solve instead. To solve a sample puzzle, use the `-n` or `--name` flags to `sudoku` to specify
the puzzle name *instead* of using the `-s` or `--sudoku` flags. An example of this usage would be
`sudoku -n hard-42` to solve the puzzle named `hard-42`. All other flags such as `-a` (see Algorithms above), `-g`
(see GUI Mode, below), and `-q` (see Output, below) are treated the same when using `-n` as when using `-s`.
For programmatic access to the sample puzzles, the `get_puzzle_by_name` function in the `sample_puzzles` module
accepts a string representing a puzzle name (see above) and returns a string representation of the corresponding
(unsolved) sudoku puzzle (see the Usage section above). For example:
```python
>>> from sudoku.sample_puzzles import get_puzzle_by_name
>>> puzzle = get_puzzle_by_name('hard-57')
>>> puzzle
'1....786...7..8.1.8..2....9........24...1......9..5...6.8..........5.9.......93.4'
```
### Output
When running in non-GUI mode (the default), the `sudoku` program prints output to the console before, during, and
after solving the given puzzle. Sample output from running the `sudoku` program on one of the included sample puzzles
(see Sample Puzzles, above) is as follows.
```
$ sudoku -n hard-25
Starting puzzle:
+-------+-------+-------+
| 1 . . | . . . | 7 . 9 |
| . 4 . | . . 7 | 2 . . |
| 8 . . | . . . | . . . |
+-------+-------+-------+
| . 7 . | . 1 . | . 6 . |
| 3 . . | . . . | . . 5 |
| . 6 . | . 4 . | . 2 . |
+-------+-------+-------+
| . . . | . . . | . . 8 |
| . . 5 | 3 . . | . 7 . |
| 7 . 2 | . . . | . 4 6 |
+-------+-------+-------+
Solving for 58 unknown cells using the constraint based algorithm...
Done! Evaluated 5 possibilities with 0 backtracks in 0.01 seconds.
+-------+-------+-------+
| 1 2 3 | 4 5 6 | 7 8 9 |
| 6 4 9 | 8 3 7 | 2 5 1 |
| 8 5 7 | 2 9 1 | 6 3 4 |
+-------+-------+-------+
| 2 7 4 | 5 1 8 | 9 6 3 |
| 3 9 8 | 6 7 2 | 4 1 5 |
| 5 6 1 | 9 4 3 | 8 2 7 |
+-------+-------+-------+
| 4 1 6 | 7 2 5 | 3 9 8 |
| 9 8 5 | 3 6 4 | 1 7 2 |
| 7 3 2 | 1 8 9 | 5 4 6 |
+-------+-------+-------+
123456789649837251857291634274518963398672415561943827416725398985364172732189546
```
Note that the real output will be colorized, with the initial clue cells of the puzzle colored cyan to differentiate
them from the cells that were solved by the program. The program currently does not support disabling colorized output.
To reduce the verbosity of the output, the program accepts a flag called `-q` (`--quiet`). This flag may be
given up to three times, with less output being printed for each additional use of the flag.
The following is a sample of the output when running with the verbosity reduced by one level.
```
$ sudoku -n hard-25 -q
Solving for 58 unknown cells using the constraint based algorithm...
Done! Evaluated 5 possibilities with 0 backtracks in 0.01 seconds.
+-------+-------+-------+
| 1 2 3 | 4 5 6 | 7 8 9 |
| 6 4 9 | 8 3 7 | 2 5 1 |
| 8 5 7 | 2 9 1 | 6 3 4 |
+-------+-------+-------+
| 2 7 4 | 5 1 8 | 9 6 3 |
| 3 9 8 | 6 7 2 | 4 1 5 |
| 5 6 1 | 9 4 3 | 8 2 7 |
+-------+-------+-------+
| 4 1 6 | 7 2 5 | 3 9 8 |
| 9 8 5 | 3 6 4 | 1 7 2 |
| 7 3 2 | 1 8 9 | 5 4 6 |
+-------+-------+-------+
123456789649837251857291634274518963398672415561943827416725398985364172732189546
```
The following is a sample of the output when running with the verbosity reduced by two levels.
```
$ sudoku -n hard-25 -qq
Solving for 58 unknown cells using the constraint based algorithm...
Done! Evaluated 5 possibilities with 0 backtracks in 0.01 seconds.
123456789649837251857291634274518963398672415561943827416725398985364172732189546
```
The following is a sample of the output when running with the verbosity reduced by three levels (the maximum).
```
$ sudoku -n hard-25 -qqq
123456789649837251857291634274518963398672415561943827416725398985364172732189546
```
When running with minimal output, the program only prints the condensed version of the solved puzzle to the console.
This output is suitable for piping to other utilities for further processing. In this way, the `sudoku` program may
be used in a shell script, pipeline, or other non-interactive environment.
When running with more than minimal output (i.e., `-q`, `-qq`, or no `-q` flag at all), the program will print a `.`
character to the console for every 1,000 possibilities it tries while attempting to solve the puzzle. For the
constraint-based algorithm (the default), the puzzle is usually solved well in advance of 1,000 possibilities being
tried. For the brute-force and DLX algorithms, however, the `.` characters serve to show that the program is still
working, since otherwise there is no way to tell if the program is doing anything (except, perhaps, by measuring
the fan speed of the computer running the program).
#### Exit Codes
When the program runs successfully, it exits with a code of zero (0). If the program encounters an error in parsing
the arguments that were passed to it, it exits with a code of one (1). If the program fails to solve the given puzzle,
it exits with a code of two (2).
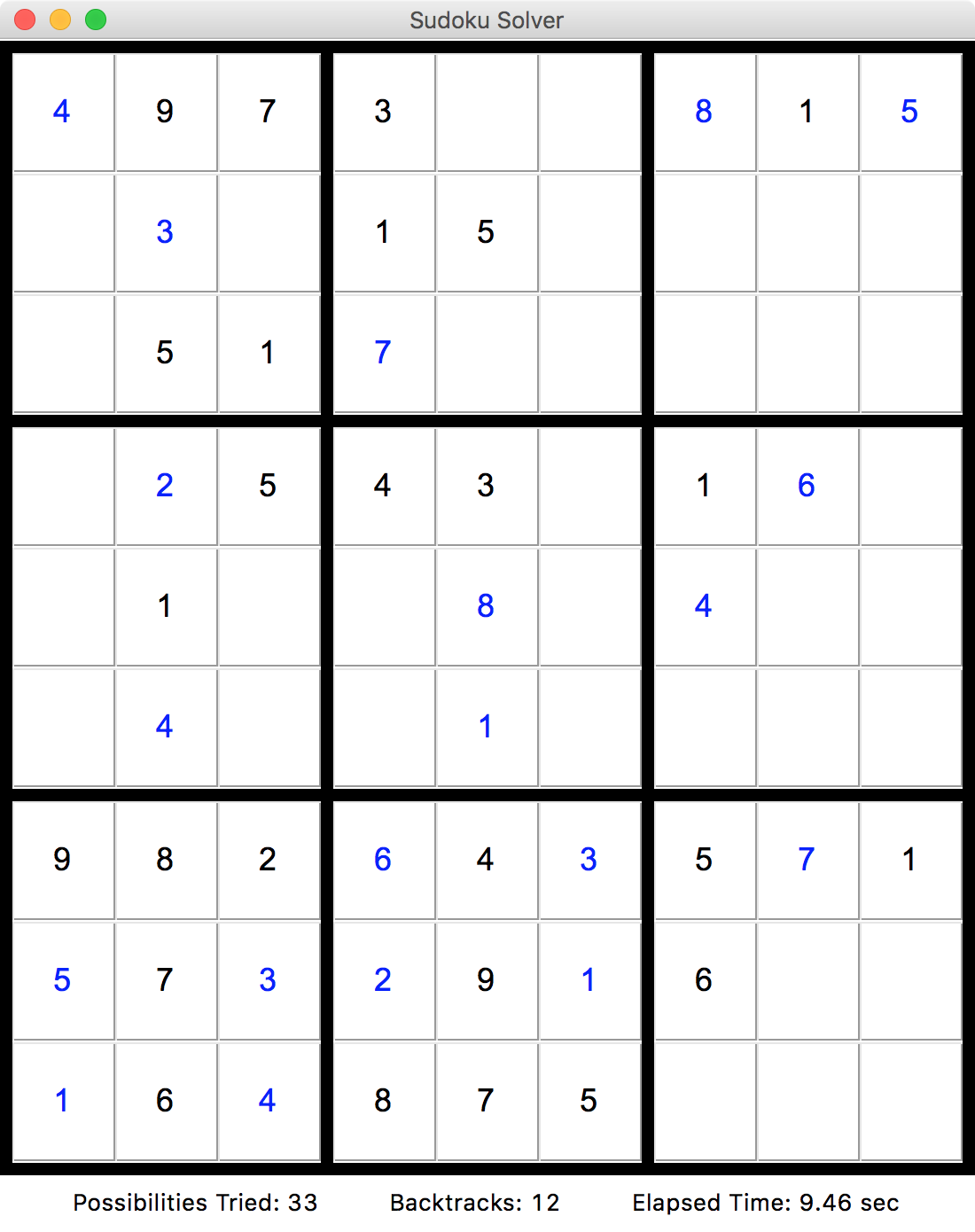
### GUI Mode
In order to help visualize the process of solving a given sudoku puzzle, the program also has a GUI mode, which can be
activated with the `-g` (`--gui`) flag to `sudoku`. When running in GUI mode, no output is printed to the console.
Instead, a window will open showing the sudoku puzzle being solved, with statistics along the bottom showing in real
time how many possibilities have been tried so far, how many times the algorithm has backtracked, and how much time
has elapsed since the solver began running.
By default, the puzzle will be solved as fast as possible, and the GUI will be updated very frequently as the solver
makes progress on solving the puzzle. However, this often means that the state of the puzzle is being updated so
quickly that it is impossible for an observer to keep up with the progress of the solver. In order to sidestep this
problem, the `-d` (`--delay`) flag to `sudoku` will delay updates to the GUI by the given number of milliseconds
at each step in the solution. For example, passing `-d 500` will pause the GUI for half a second (500 milliseconds)
after each time the puzzle is changed. This makes it far easier to understand what is happening at each step in the
solving process. (Note that, even with no artificial delay, it will take slightly longer to solve a given puzzle in
GUI mode than it will to solve the same puzzle in non-GUI mode.)
Unfortunately, the DLX algorithm does not lend itself to being visualized with a constantly-updating sudoku puzzle.
This is because the DLX algorithm transforms the problem of solving a sudoku into a different type of problem
involving constraint sets and matrices, and the underlying relationship to a sudoku puzzle is obscured at best. For
this reason, **GUI mode is not available when using the DLX algorithm**.
A sample of the program running in GUI mode is shown below.
Raw data
{
"_id": null,
"home_page": "https://github.com/will2dye4/sudoku.git",
"name": "sudoku-ui",
"maintainer": "",
"docs_url": null,
"requires_python": ">=3.7,<4.0",
"maintainer_email": "",
"keywords": "dancing links,dlx,sudoku,sudoku solver",
"author": "William Dye",
"author_email": "",
"download_url": "https://files.pythonhosted.org/packages/ed/75/2c5611730e1b736fe89ac6dc158bad25d02f92e9444c600ba9b8cd438b89/sudoku_ui-1.0.3.tar.gz",
"platform": null,
"description": "# sudoku - Python sudoku solver\n\nThis package contains utilities for solving [sudoku](https://en.wikipedia.org/wiki/Sudoku) puzzles\nusing a variety of different algorithms.\n\n## Installation\n\nThe easiest way to install the package is to download it from [PyPI](https://pypi.org) using `pip`.\nNote that `sudoku` depends on [Python](https://www.python.org/downloads/) 3.7 or newer; please\nensure that you have a semi-recent version of Python installed before proceeding.\n\nRun the following command in a shell (a UNIX-like environment is assumed):\n\n```\n$ pip install sudoku-ui\n```\n\nThe package does not have any dependencies besides Python itself. If you wish to sandbox your\ninstallation inside a virtual environment, you may choose to use\n[virtualenvwrapper](https://virtualenvwrapper.readthedocs.io/en/latest/) or a similar\nutility to do so.\n\nWhen successfully installed, a program called `sudoku` will be placed on your `PATH`. See the\nUsage section below for details about how to use this program.\n\n## Usage\n\nAt any time, you can use the `-h` or `--help` flags to see a summary of options that the program accepts.\n\n```\n$ sudoku -h\nusage: sudoku [-h] [-s SUDOKU] [-n NAME] [-a {brute-force,constraint,dlx}] [-g] [-d DELAY] [-q]\n\nSolve sudoku puzzles.\n\noptional arguments:\n -h, --help show this help message and exit\n -s SUDOKU, --sudoku SUDOKU, --string SUDOKU, --sudoku-string SUDOKU\n A string representing a sudoku puzzle to solve\n -n NAME, --name NAME The name of a sample puzzle to solve (for demo purposes)\n -a {brute-force,constraint,dlx}, --algorithm {brute-force,constraint,dlx}\n The algorithm to use to solve the puzzle\n -g, --gui, --ui Display a GUI showing the puzzle being solved (not available for DLX mode)\n -d DELAY, --delay DELAY, --delay-millis DELAY\n How long to delay between steps in solving the puzzle (only applies in GUI mode)\n -q, --quiet Reduce output verbosity (may be used multiple times)\n```\n\nThe most basic usage is `sudoku -s <string>`, where `<string>` is a string representing a sudoku\npuzzle to solve. The string should contain the value for each cell in the puzzle as a digit, or\na `0` or `.` for cells that are empty. Any other characters in the string will be ignored. For\nexample, the following three strings all represent the same puzzle to the program:\n\n```\n4.....8.5.3..........7......2.....6.....8.4......1.......6.3.7.5..2.....1.4......\n```\n\n```\n400000805\n030000000\n000700000\n020000060\n000080400\n000010000\n000603070\n500200000\n104000000\n```\n\n```\n4 . . |. . . |8 . 5 \n. 3 . |. . . |. . . \n. . . |7 . . |. . . \n------+------+------\n. 2 . |. . . |. 6 . \n. . . |. 8 . |4 . . \n. . . |. 1 . |. . . \n------+------+------\n. . . |6 . 3 |. 7 . \n5 . . |2 . . |. . . \n1 . 4 |. . . |. . . \n```\n\n### Algorithms\n\nBy default, `sudoku` will use its fastest algorithm to solve the puzzle. This is a \n**constraint-based** algorithm which uses the rules of sudoku to quickly deduce the solution\nto any input puzzle (assuming the puzzle has enough clues to be solved). The constraint-based\nalgorithm typically solves a sudoku in about 0.1 seconds (tested on a mid-2015 MacBook Pro).\nThe implementation of the constraint-based solution algorithm is based heavily on the [prior work \nof Peter Norvig](http://norvig.com/sudoku.html).\n\nTo specify a different algorithm, use the `-a` or `--algorithm` flags to `sudoku`. The other\navailable algorithms are `brute-force` and `dlx`. A description of each of these algorithms follows.\n\nThe **brute-force** algorithm tries all possible values for all empty cells in the puzzle, and \ntherefore its running time is exponential in the number of empty cells, i.e., *O(9^n)* where\n*n* is the number of empty cells. Given a sudoku puzzle designed specifically to thwart the brute-force\nstrategy, this algorithm could take longer than the lifetime of the universe to find the solution!\nIn practice, however, this algorithm typically takes about 10 minutes to solve even a fairly hard sudoku.\n\nThe **DLX** algorithm uses the [\"dancing links\" algorithm](https://arxiv.org/pdf/cs/0011047.pdf) (due to \nDon Knuth) to solve a sudoku puzzle by mapping it onto an equivalent [exact cover](https://en.wikipedia.org/wiki/Exact_cover)\nproblem and using a Python implementation of dancing links to solve the exact cover problem. This \nalgorithm by far the slowest of the three, often taking over a day to solve a typical input puzzle.\nProfiling is needed to figure out where this algorithm is spending all of its time, since in theory this\nstrategy should be at least as efficient (if not more efficient) than the brute-force approach.\nA re-implementation of the DLX algorithm in [Go](https://golang.org) may be developed at some point \nin order to compare its performance against the (slow) Python implementation found here. \n\n### Sample Puzzles\n\nThe `sudoku.sample_puzzles` module provides some sample sudoku puzzles for purposes of demoing or\ntesting the sudoku solver. The following puzzles are available:\n\n* **empty-*n*** (1 ≤ *n* ≤ 64) - a sudoku puzzle with *n* empty cells (the remaining cells are already solved \n with the correct values); these are useful for functional and performance testing of the slower algorithms\n* **hard-*n*** (1 ≤ *n* ≤ 95) - a hard sudoku puzzle with only the initial clue cells already solved\n\nInstead of providing a sudoku string to solve when running the `sudoku` program, you may instead provide the name\nof a sample puzzle to solve instead. To solve a sample puzzle, use the `-n` or `--name` flags to `sudoku` to specify\nthe puzzle name *instead* of using the `-s` or `--sudoku` flags. An example of this usage would be\n`sudoku -n hard-42` to solve the puzzle named `hard-42`. All other flags such as `-a` (see Algorithms above), `-g`\n(see GUI Mode, below), and `-q` (see Output, below) are treated the same when using `-n` as when using `-s`. \n\nFor programmatic access to the sample puzzles, the `get_puzzle_by_name` function in the `sample_puzzles` module \naccepts a string representing a puzzle name (see above) and returns a string representation of the corresponding \n(unsolved) sudoku puzzle (see the Usage section above). For example:\n\n```python\n>>> from sudoku.sample_puzzles import get_puzzle_by_name\n>>> puzzle = get_puzzle_by_name('hard-57')\n>>> puzzle\n'1....786...7..8.1.8..2....9........24...1......9..5...6.8..........5.9.......93.4'\n```\n\n### Output\n\nWhen running in non-GUI mode (the default), the `sudoku` program prints output to the console before, during, and\nafter solving the given puzzle. Sample output from running the `sudoku` program on one of the included sample puzzles\n(see Sample Puzzles, above) is as follows.\n\n```\n$ sudoku -n hard-25\nStarting puzzle:\n+-------+-------+-------+\n| 1 . . | . . . | 7 . 9 |\n| . 4 . | . . 7 | 2 . . |\n| 8 . . | . . . | . . . |\n+-------+-------+-------+\n| . 7 . | . 1 . | . 6 . |\n| 3 . . | . . . | . . 5 |\n| . 6 . | . 4 . | . 2 . |\n+-------+-------+-------+\n| . . . | . . . | . . 8 |\n| . . 5 | 3 . . | . 7 . |\n| 7 . 2 | . . . | . 4 6 |\n+-------+-------+-------+\n\nSolving for 58 unknown cells using the constraint based algorithm...\nDone! Evaluated 5 possibilities with 0 backtracks in 0.01 seconds.\n\n+-------+-------+-------+\n| 1 2 3 | 4 5 6 | 7 8 9 |\n| 6 4 9 | 8 3 7 | 2 5 1 |\n| 8 5 7 | 2 9 1 | 6 3 4 |\n+-------+-------+-------+\n| 2 7 4 | 5 1 8 | 9 6 3 |\n| 3 9 8 | 6 7 2 | 4 1 5 |\n| 5 6 1 | 9 4 3 | 8 2 7 |\n+-------+-------+-------+\n| 4 1 6 | 7 2 5 | 3 9 8 |\n| 9 8 5 | 3 6 4 | 1 7 2 |\n| 7 3 2 | 1 8 9 | 5 4 6 |\n+-------+-------+-------+\n\n123456789649837251857291634274518963398672415561943827416725398985364172732189546\n```\n\nNote that the real output will be colorized, with the initial clue cells of the puzzle colored cyan to differentiate \nthem from the cells that were solved by the program. The program currently does not support disabling colorized output.\n\nTo reduce the verbosity of the output, the program accepts a flag called `-q` (`--quiet`). This flag may be\ngiven up to three times, with less output being printed for each additional use of the flag.\n\nThe following is a sample of the output when running with the verbosity reduced by one level.\n\n```\n$ sudoku -n hard-25 -q\nSolving for 58 unknown cells using the constraint based algorithm...\nDone! Evaluated 5 possibilities with 0 backtracks in 0.01 seconds.\n\n+-------+-------+-------+\n| 1 2 3 | 4 5 6 | 7 8 9 |\n| 6 4 9 | 8 3 7 | 2 5 1 |\n| 8 5 7 | 2 9 1 | 6 3 4 |\n+-------+-------+-------+\n| 2 7 4 | 5 1 8 | 9 6 3 |\n| 3 9 8 | 6 7 2 | 4 1 5 |\n| 5 6 1 | 9 4 3 | 8 2 7 |\n+-------+-------+-------+\n| 4 1 6 | 7 2 5 | 3 9 8 |\n| 9 8 5 | 3 6 4 | 1 7 2 |\n| 7 3 2 | 1 8 9 | 5 4 6 |\n+-------+-------+-------+\n\n123456789649837251857291634274518963398672415561943827416725398985364172732189546\n```\n\nThe following is a sample of the output when running with the verbosity reduced by two levels.\n\n```\n$ sudoku -n hard-25 -qq\nSolving for 58 unknown cells using the constraint based algorithm...\nDone! Evaluated 5 possibilities with 0 backtracks in 0.01 seconds.\n\n123456789649837251857291634274518963398672415561943827416725398985364172732189546\n```\n\nThe following is a sample of the output when running with the verbosity reduced by three levels (the maximum).\n\n```\n$ sudoku -n hard-25 -qqq\n123456789649837251857291634274518963398672415561943827416725398985364172732189546\n```\n\nWhen running with minimal output, the program only prints the condensed version of the solved puzzle to the console.\nThis output is suitable for piping to other utilities for further processing. In this way, the `sudoku` program may\nbe used in a shell script, pipeline, or other non-interactive environment.\n\nWhen running with more than minimal output (i.e., `-q`, `-qq`, or no `-q` flag at all), the program will print a `.`\ncharacter to the console for every 1,000 possibilities it tries while attempting to solve the puzzle. For the\nconstraint-based algorithm (the default), the puzzle is usually solved well in advance of 1,000 possibilities being\ntried. For the brute-force and DLX algorithms, however, the `.` characters serve to show that the program is still\nworking, since otherwise there is no way to tell if the program is doing anything (except, perhaps, by measuring\nthe fan speed of the computer running the program).\n\n#### Exit Codes\n\nWhen the program runs successfully, it exits with a code of zero (0). If the program encounters an error in parsing\nthe arguments that were passed to it, it exits with a code of one (1). If the program fails to solve the given puzzle,\nit exits with a code of two (2).\n\n### GUI Mode\n\nIn order to help visualize the process of solving a given sudoku puzzle, the program also has a GUI mode, which can be\nactivated with the `-g` (`--gui`) flag to `sudoku`. When running in GUI mode, no output is printed to the console.\nInstead, a window will open showing the sudoku puzzle being solved, with statistics along the bottom showing in real\ntime how many possibilities have been tried so far, how many times the algorithm has backtracked, and how much time\nhas elapsed since the solver began running.\n\nBy default, the puzzle will be solved as fast as possible, and the GUI will be updated very frequently as the solver\nmakes progress on solving the puzzle. However, this often means that the state of the puzzle is being updated so\nquickly that it is impossible for an observer to keep up with the progress of the solver. In order to sidestep this\nproblem, the `-d` (`--delay`) flag to `sudoku` will delay updates to the GUI by the given number of milliseconds\nat each step in the solution. For example, passing `-d 500` will pause the GUI for half a second (500 milliseconds)\nafter each time the puzzle is changed. This makes it far easier to understand what is happening at each step in the\nsolving process. (Note that, even with no artificial delay, it will take slightly longer to solve a given puzzle in\nGUI mode than it will to solve the same puzzle in non-GUI mode.)\n\nUnfortunately, the DLX algorithm does not lend itself to being visualized with a constantly-updating sudoku puzzle.\nThis is because the DLX algorithm transforms the problem of solving a sudoku into a different type of problem\ninvolving constraint sets and matrices, and the underlying relationship to a sudoku puzzle is obscured at best. For\nthis reason, **GUI mode is not available when using the DLX algorithm**.\n\nA sample of the program running in GUI mode is shown below.\n\n\n",
"bugtrack_url": null,
"license": "MIT",
"summary": "Solve sudoku puzzles using various algorithms",
"version": "1.0.3",
"project_urls": {
"Homepage": "https://github.com/will2dye4/sudoku.git",
"Repository": "https://github.com/will2dye4/sudoku.git"
},
"split_keywords": [
"dancing links",
"dlx",
"sudoku",
"sudoku solver"
],
"urls": [
{
"comment_text": "",
"digests": {
"blake2b_256": "9bf9d0eb126a4e0dcf5093e0aed3f0612713531a694fccaef9e1464182d65dca",
"md5": "89e124b0da6935a652d9d2553b35e84f",
"sha256": "d3d63577e1dccce33c91adf66bfdf2d7952058216d31a0150a81a2748355a06c"
},
"downloads": -1,
"filename": "sudoku_ui-1.0.3-py3-none-any.whl",
"has_sig": false,
"md5_digest": "89e124b0da6935a652d9d2553b35e84f",
"packagetype": "bdist_wheel",
"python_version": "py3",
"requires_python": ">=3.7,<4.0",
"size": 25048,
"upload_time": "2023-09-19T20:18:06",
"upload_time_iso_8601": "2023-09-19T20:18:06.315124Z",
"url": "https://files.pythonhosted.org/packages/9b/f9/d0eb126a4e0dcf5093e0aed3f0612713531a694fccaef9e1464182d65dca/sudoku_ui-1.0.3-py3-none-any.whl",
"yanked": false,
"yanked_reason": null
},
{
"comment_text": "",
"digests": {
"blake2b_256": "ed752c5611730e1b736fe89ac6dc158bad25d02f92e9444c600ba9b8cd438b89",
"md5": "bfc016e1e056c143c91bfc511bb286b5",
"sha256": "e4de7a11edbe4b2768222166ca3f28067a378f95bc281fdef97d446fcce18148"
},
"downloads": -1,
"filename": "sudoku_ui-1.0.3.tar.gz",
"has_sig": false,
"md5_digest": "bfc016e1e056c143c91bfc511bb286b5",
"packagetype": "sdist",
"python_version": "source",
"requires_python": ">=3.7,<4.0",
"size": 25691,
"upload_time": "2023-09-19T20:18:07",
"upload_time_iso_8601": "2023-09-19T20:18:07.882133Z",
"url": "https://files.pythonhosted.org/packages/ed/75/2c5611730e1b736fe89ac6dc158bad25d02f92e9444c600ba9b8cd438b89/sudoku_ui-1.0.3.tar.gz",
"yanked": false,
"yanked_reason": null
}
],
"upload_time": "2023-09-19 20:18:07",
"github": true,
"gitlab": false,
"bitbucket": false,
"codeberg": false,
"github_user": "will2dye4",
"github_project": "sudoku",
"travis_ci": false,
"coveralls": false,
"github_actions": false,
"lcname": "sudoku-ui"
}
