| Name | torch-fem JSON |
| Version |
0.3.8
 JSON
JSON |
| download |
| home_page | None |
| Summary | GPU accelerated differential finite elements for solid mechanics with PyTorch. |
| upload_time | 2025-02-10 08:03:30 |
| maintainer | None |
| docs_url | None |
| author | None |
| requires_python | >=3.10 |
| license | Copyright 2024 Nils Meyer
Permission is hereby granted, free of charge, to any person obtaining a copy of this software and associated documentation files (the “Software”), to deal in the Software without restriction, including without limitation the rights to use, copy, modify, merge, publish, distribute, sublicense, and/or sell copies of the Software, and to permit persons to whom the Software is furnished to do so, subject to the following conditions:
The above copyright notice and this permission notice shall be included in all copies or substantial portions of the Software.
THE SOFTWARE IS PROVIDED “AS IS”, WITHOUT WARRANTY OF ANY KIND, EXPRESS OR IMPLIED, INCLUDING BUT NOT LIMITED TO THE WARRANTIES OF MERCHANTABILITY, FITNESS FOR A PARTICULAR PURPOSE AND NONINFRINGEMENT. IN NO EVENT SHALL THE AUTHORS OR COPYRIGHT HOLDERS BE LIABLE FOR ANY CLAIM, DAMAGES OR OTHER LIABILITY, WHETHER IN AN ACTION OF CONTRACT, TORT OR OTHERWISE, ARISING FROM, OUT OF OR IN CONNECTION WITH THE SOFTWARE OR THE USE OR OTHER DEALINGS IN THE SOFTWARE. |
| keywords |
finite elements
automatic differentiation
|
| VCS |
 |
| bugtrack_url |
|
| requirements |
No requirements were recorded.
|
| Travis-CI |
No Travis.
|
| coveralls test coverage |
No coveralls.
|
[](https://opensource.org/licenses/MIT)

[](https://pypi.org/project/torch-fem/)
[](https://github.com/psf/black)
[](https://mybinder.org/v2/gh/meyer-nils/torch-fem/HEAD)
# torch-fem
Simple GPU accelerated differentiable finite elements for small-deformation solid mechanics with PyTorch.
PyTorch enables efficient computation of sensitivities via automatic differentiation and using them in optimization tasks.
## Installation
Your may install torch-fem via pip with
```
pip install torch-fem
```
*Optional*: For GPU support, install CUDA and the corresponding CuPy version with
```
pip install cupy-cuda11x # v11.2 - 11.8
pip install cupy-cuda12x # v12.x
```
## Features
- Elements
- 1D: Bar1, Bar2
- 2D: Quad1, Quad2, Tria1, Tria2
- 3D: Hexa1, Hexa2, Tetra1, Tetra2
- Shell: Flat-facet triangle (linear only)
- Material models (3D, 2D plane stress, 2D plane strain, 1D)
- Isotropic linear elasticity
- Orthotropic linear elasticity
- Isotropic plasticity
- Utilities
- Homogenization of orthotropic stiffness
- I/O to and from other mesh formats via meshio
## Basic examples
The subdirectory `examples->basic` contains a couple of Jupyter Notebooks demonstrating the use of torch-fem for trusses, planar problems, shells and solids. You may click on the examples to check out the notebooks online.
<table>
<tbody>
<tr>
<td style="width: 30%;"><a href="https://meyer-nils.github.io/torch-fem/examples/basic/solid/gyroid.html"><img src="https://meyer-nils.github.io/torch-fem/gyroid.png"></a></td>
<td style="width: 30%;"><a href="https://meyer-nils.github.io/torch-fem/examples/basic/solid/cubes.html"><img src="https://meyer-nils.github.io/torch-fem/cubes.png"></a></td>
<td style="width: 30%;"><a href="https://meyer-nils.github.io/torch-fem/examples/basic/planar/cantilever.html"><img src="https://meyer-nils.github.io/torch-fem/cantilever_tria2.png"></a></td>
</tr>
<tr>
<td align="center"><b>Gyroid:</b> Support for voxel meshes and implicit surfaces.</td>
<td align="center"><b>Solid cubes:</b> There are several examples with different element types rendered in PyVista.</td>
<td align="center"><b>Planar cantilever beams:</b> There are several examples with different element types rendered in matplotlib.</td>
</tr>
<tr>
<td colspan="3"><a href="https://meyer-nils.github.io/torch-fem/examples/basic/planar/plasticity.html"><img src="https://meyer-nils.github.io/torch-fem/plate_hole_plasticity.png"></a></td>
</tr>
<tr>
<td colspan="3" align="center"><b>Plasticity in a plate with hole:</b> Isotropic linear hardening model for plane-stress or plane-strain.</td>
</tr>
</tbody>
</table>
## Optimization examples
The subdirectory `examples->optimization` demonstrates the use of torch-fem for optimization of structures (e.g. topology optimization, composite orientation optimization). You may click on the examples to check out the notebooks online.
<table>
<tbody>
<tr>
<td style="width: 50%;"><a href="https://meyer-nils.github.io/torch-fem/examples/optimization/truss/shape.html"><img src="https://meyer-nils.github.io/torch-fem/bridge.png"></a></td>
<td style="width: 50%;"><a href="https://meyer-nils.github.io/torch-fem/examples/optimization/planar/shape.html"><img src="https://meyer-nils.github.io/torch-fem/fillet_shape_optimization.png"></a></td>
</tr>
<tr>
<td align="center"><b>Shape optimization of a truss:</b> The top nodes are moved and MMA + autograd is used to minimize the compliance.</td>
<td align="center"><b>Shape optimization of a fillet:</b> The shape is morphed with shape basis vectors and MMA + autograd is used to minimize the maximum stress.</td>
</tr>
<tr>
<td style="width: 50%;"><a href="https://meyer-nils.github.io/torch-fem/examples/optimization/planar/topology.html"><img src="https://meyer-nils.github.io/torch-fem/topopt_mbb.png"></a></td>
<td style="width: 50%;"><img src="https://meyer-nils.github.io/torch-fem/topopt_3d.png"></td>
</tr>
<tr>
<td align="center"><b>Topology optimization of a MBB beam:</b> You can switch between analytical and autograd sensitivities.</td>
<td align="center"><b>Topology optimization of a jet engine bracket:</b> The 3D model is exported to Paraview for visualization.</td>
</tr>
<tr>
<td style="width: 50%;"><a href="https://meyer-nils.github.io/torch-fem/examples/optimization/planar/topology+orientation.html"><img src="https://meyer-nils.github.io/torch-fem/topo+ori.png"></a></td>
<td style="width: 50%;"><a href="https://meyer-nils.github.io/torch-fem/examples/optimization/planar/orientation.html"><img src="https://meyer-nils.github.io/torch-fem/plate_hole_shape_optimization.png"></a>
</td>
</tr>
<tr>
<td align="center"><b>Combined topology and orientation optimization:</b> Compliance is minimized by optimizing fiber orientation and density of an anisotropic material using automatic differentiation.</td>
<td align="center"><b>Fiber orientation optimization of a plate with a hole</b> Compliance is minimized by optimizing the fiber orientation of an anisotropic material using automatic differentiation w.r.t. element-wise fiber angles.</td>
</tr>
</tbody>
</table>
## Minimal example
This is a minimal example of how to use torch-fem to solve a very simple planar cantilever problem.
```python
import torch
from torchfem import Planar
from torchfem.materials import IsotropicElasticityPlaneStress
torch.set_default_dtype(torch.float64)
# Material
material = IsotropicElasticityPlaneStress(E=1000.0, nu=0.3)
# Nodes and elements
nodes = torch.tensor([[0., 0.], [1., 0.], [2., 0.], [0., 1.], [1., 1.], [2., 1.]])
elements = torch.tensor([[0, 1, 4, 3], [1, 2, 5, 4]])
# Create model
cantilever = Planar(nodes, elements, material)
# Load at tip [Node_ID, DOF]
cantilever.forces[5, 1] = -1.0
# Constrained displacement at left end [Node_IDs, DOFs]
cantilever.constraints[[0, 3], :] = True
# Show model
cantilever.plot(node_markers="o", node_labels=True)
```
This creates a minimal planar FEM model:
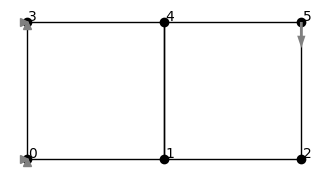
```python
# Solve
u, f, σ, ε, α = cantilever.solve()
# Plot displacement magnitude on deformed state
cantilever.plot(u, node_property=torch.norm(u, dim=1))
```
This solves the model and plots the result:
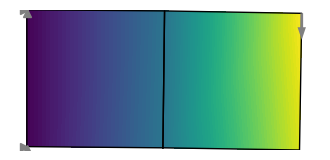
If we want to compute gradients through the FEM model, we simply need to define the variables that require gradients. Automatic differentiation is performed through the entire FE solver.
```python
# Enable automatic differentiation
cantilever.thickness.requires_grad = True
u, f, _, _, _ = cantilever.solve()
# Compute sensitivity of compliance w.r.t. element thicknesses
compliance = torch.inner(f.ravel(), u.ravel())
torch.autograd.grad(compliance, cantilever.thickness)[0]
```
## Benchmarks
The following benchmarks were performed on a cube subjected to a one-dimensional extension. The cube is discretized with N x N x N linear hexahedral elements, has a side length of 1.0 and is made of a material with Young's modulus of 1000.0 and Poisson's ratio of 0.3. The cube is fixed at one end and a displacement of 0.1 is applied at the other end. The benchmark measures the forward time to assemble the stiffness matrix and the time to solve the linear system. In addition, it measures the backward time to compute the sensitivities of the sum of displacements with respect to forces.
#### Apple M1 Pro (10 cores, 16 GB RAM)
Python 3.10, SciPy 1.14.1, Apple Accelerate
| N | DOFs | FWD Time | BWD Time | Peak RAM |
| --- | -------- | --------- | --------- | ---------- |
| 10 | 3000 | 0.14s | 0.03s | 592.2MB |
| 20 | 24000 | 0.99s | 0.15s | 968.3MB |
| 30 | 81000 | 3.42s | 0.57s | 1562.8MB |
| 40 | 192000 | 8.48s | 1.14s | 2497.1MB |
| 50 | 375000 | 16.46s | 2.23s | 3963.7MB |
| 60 | 648000 | 28.63s | 3.56s | 5503.3MB |
| 70 | 1029000 | 46.86s | 5.91s | 6309.5MB |
| 80 | 1536000 | 74.12s | 10.69s | 6933.7MB |
| 90 | 2187000 | 121.11s | 16.63s | 7663.5MB |
| 100 | 3000000 | 179.44s | 38.35s | 9662.4MB |
#### AMD Ryzen Threadripper PRO 5995WX (64 Cores, 512 GB RAM) and NVIDIA GeForce RTX 4090
Python 3.12, CuPy 13.3.0, CUDA 11.8
| N | DOFs | FWD Time | BWD Time | Peak RAM |
| --- | -------- | --------- | --------- | ---------- |
| 10 | 3000 | 0.66s | 0.15s | 1371.7MB |
| 20 | 24000 | 1.00s | 0.43s | 1358.9MB |
| 30 | 81000 | 1.14s | 0.65s | 1371.1MB |
| 40 | 192000 | 1.37s | 0.83s | 1367.3MB |
| 50 | 375000 | 1.51s | 1.04s | 1356.4MB |
| 60 | 648000 | 1.94s | 1.43s | 1342.1MB |
| 70 | 1029000 | 5.19s | 4.31s | 1366.8MB |
| 80 | 1536000 | 7.48s | 18.88s | 5105.6MB |
Raw data
{
"_id": null,
"home_page": null,
"name": "torch-fem",
"maintainer": null,
"docs_url": null,
"requires_python": ">=3.10",
"maintainer_email": null,
"keywords": "finite elements, automatic differentiation",
"author": null,
"author_email": "Nils Meyer <nils.meyer@uni-a.de>",
"download_url": "https://files.pythonhosted.org/packages/4c/56/05cface4b425d2a90f505a2698118928c8083913883d4db056f62ddea1a7/torch_fem-0.3.8.tar.gz",
"platform": null,
"description": "[](https://opensource.org/licenses/MIT)\n\n[](https://pypi.org/project/torch-fem/)\n[](https://github.com/psf/black)\n[](https://mybinder.org/v2/gh/meyer-nils/torch-fem/HEAD)\n\n\n# torch-fem\nSimple GPU accelerated differentiable finite elements for small-deformation solid mechanics with PyTorch. \nPyTorch enables efficient computation of sensitivities via automatic differentiation and using them in optimization tasks.\n\n## Installation\nYour may install torch-fem via pip with\n```\npip install torch-fem\n```\n\n*Optional*: For GPU support, install CUDA and the corresponding CuPy version with\n```\npip install cupy-cuda11x # v11.2 - 11.8\npip install cupy-cuda12x # v12.x\n```\n\n## Features\n- Elements\n - 1D: Bar1, Bar2\n - 2D: Quad1, Quad2, Tria1, Tria2\n - 3D: Hexa1, Hexa2, Tetra1, Tetra2\n - Shell: Flat-facet triangle (linear only)\n- Material models (3D, 2D plane stress, 2D plane strain, 1D)\n - Isotropic linear elasticity \n - Orthotropic linear elasticity\n - Isotropic plasticity\n- Utilities\n - Homogenization of orthotropic stiffness\n - I/O to and from other mesh formats via meshio\n\n## Basic examples\nThe subdirectory `examples->basic` contains a couple of Jupyter Notebooks demonstrating the use of torch-fem for trusses, planar problems, shells and solids. You may click on the examples to check out the notebooks online.\n\n<table>\n <tbody>\n <tr>\n <td style=\"width: 30%;\"><a href=\"https://meyer-nils.github.io/torch-fem/examples/basic/solid/gyroid.html\"><img src=\"https://meyer-nils.github.io/torch-fem/gyroid.png\"></a></td>\n <td style=\"width: 30%;\"><a href=\"https://meyer-nils.github.io/torch-fem/examples/basic/solid/cubes.html\"><img src=\"https://meyer-nils.github.io/torch-fem/cubes.png\"></a></td>\n <td style=\"width: 30%;\"><a href=\"https://meyer-nils.github.io/torch-fem/examples/basic/planar/cantilever.html\"><img src=\"https://meyer-nils.github.io/torch-fem/cantilever_tria2.png\"></a></td>\n </tr>\n <tr>\n <td align=\"center\"><b>Gyroid:</b> Support for voxel meshes and implicit surfaces.</td>\n <td align=\"center\"><b>Solid cubes:</b> There are several examples with different element types rendered in PyVista.</td>\n <td align=\"center\"><b>Planar cantilever beams:</b> There are several examples with different element types rendered in matplotlib.</td>\n </tr>\n <tr>\n <td colspan=\"3\"><a href=\"https://meyer-nils.github.io/torch-fem/examples/basic/planar/plasticity.html\"><img src=\"https://meyer-nils.github.io/torch-fem/plate_hole_plasticity.png\"></a></td>\n </tr>\n <tr>\n <td colspan=\"3\" align=\"center\"><b>Plasticity in a plate with hole:</b> Isotropic linear hardening model for plane-stress or plane-strain.</td>\n </tr>\n </tbody>\n</table>\n\n## Optimization examples\nThe subdirectory `examples->optimization` demonstrates the use of torch-fem for optimization of structures (e.g. topology optimization, composite orientation optimization). You may click on the examples to check out the notebooks online.\n\n<table>\n <tbody>\n <tr>\n <td style=\"width: 50%;\"><a href=\"https://meyer-nils.github.io/torch-fem/examples/optimization/truss/shape.html\"><img src=\"https://meyer-nils.github.io/torch-fem/bridge.png\"></a></td>\n <td style=\"width: 50%;\"><a href=\"https://meyer-nils.github.io/torch-fem/examples/optimization/planar/shape.html\"><img src=\"https://meyer-nils.github.io/torch-fem/fillet_shape_optimization.png\"></a></td>\n </tr>\n <tr>\n <td align=\"center\"><b>Shape optimization of a truss:</b> The top nodes are moved and MMA + autograd is used to minimize the compliance.</td>\n <td align=\"center\"><b>Shape optimization of a fillet:</b> The shape is morphed with shape basis vectors and MMA + autograd is used to minimize the maximum stress.</td>\n </tr>\n <tr>\n <td style=\"width: 50%;\"><a href=\"https://meyer-nils.github.io/torch-fem/examples/optimization/planar/topology.html\"><img src=\"https://meyer-nils.github.io/torch-fem/topopt_mbb.png\"></a></td>\n <td style=\"width: 50%;\"><img src=\"https://meyer-nils.github.io/torch-fem/topopt_3d.png\"></td>\n </tr>\n <tr>\n <td align=\"center\"><b>Topology optimization of a MBB beam:</b> You can switch between analytical and autograd sensitivities.</td>\n <td align=\"center\"><b>Topology optimization of a jet engine bracket:</b> The 3D model is exported to Paraview for visualization.</td>\n </tr>\n <tr>\n <td style=\"width: 50%;\"><a href=\"https://meyer-nils.github.io/torch-fem/examples/optimization/planar/topology+orientation.html\"><img src=\"https://meyer-nils.github.io/torch-fem/topo+ori.png\"></a></td>\n <td style=\"width: 50%;\"><a href=\"https://meyer-nils.github.io/torch-fem/examples/optimization/planar/orientation.html\"><img src=\"https://meyer-nils.github.io/torch-fem/plate_hole_shape_optimization.png\"></a>\n </td>\n </tr>\n <tr>\n <td align=\"center\"><b>Combined topology and orientation optimization:</b> Compliance is minimized by optimizing fiber orientation and density of an anisotropic material using automatic differentiation.</td>\n <td align=\"center\"><b>Fiber orientation optimization of a plate with a hole</b> Compliance is minimized by optimizing the fiber orientation of an anisotropic material using automatic differentiation w.r.t. element-wise fiber angles.</td>\n </tr>\n </tbody>\n</table>\n\n\n## Minimal example\nThis is a minimal example of how to use torch-fem to solve a very simple planar cantilever problem. \n\n```python\nimport torch\nfrom torchfem import Planar\nfrom torchfem.materials import IsotropicElasticityPlaneStress\n\ntorch.set_default_dtype(torch.float64)\n\n# Material\nmaterial = IsotropicElasticityPlaneStress(E=1000.0, nu=0.3)\n\n# Nodes and elements\nnodes = torch.tensor([[0., 0.], [1., 0.], [2., 0.], [0., 1.], [1., 1.], [2., 1.]])\nelements = torch.tensor([[0, 1, 4, 3], [1, 2, 5, 4]])\n\n# Create model\ncantilever = Planar(nodes, elements, material)\n\n# Load at tip [Node_ID, DOF]\ncantilever.forces[5, 1] = -1.0\n\n# Constrained displacement at left end [Node_IDs, DOFs]\ncantilever.constraints[[0, 3], :] = True\n\n# Show model\ncantilever.plot(node_markers=\"o\", node_labels=True)\n```\nThis creates a minimal planar FEM model:\n\n\n\n```python\n# Solve\nu, f, \u03c3, \u03b5, \u03b1 = cantilever.solve()\n\n# Plot displacement magnitude on deformed state\ncantilever.plot(u, node_property=torch.norm(u, dim=1))\n```\nThis solves the model and plots the result:\n\n\n\nIf we want to compute gradients through the FEM model, we simply need to define the variables that require gradients. Automatic differentiation is performed through the entire FE solver.\n```python \n# Enable automatic differentiation\ncantilever.thickness.requires_grad = True\nu, f, _, _, _ = cantilever.solve()\n\n# Compute sensitivity of compliance w.r.t. element thicknesses\ncompliance = torch.inner(f.ravel(), u.ravel())\ntorch.autograd.grad(compliance, cantilever.thickness)[0]\n```\n\n## Benchmarks \nThe following benchmarks were performed on a cube subjected to a one-dimensional extension. The cube is discretized with N x N x N linear hexahedral elements, has a side length of 1.0 and is made of a material with Young's modulus of 1000.0 and Poisson's ratio of 0.3. The cube is fixed at one end and a displacement of 0.1 is applied at the other end. The benchmark measures the forward time to assemble the stiffness matrix and the time to solve the linear system. In addition, it measures the backward time to compute the sensitivities of the sum of displacements with respect to forces.\n\n#### Apple M1 Pro (10 cores, 16 GB RAM)\nPython 3.10, SciPy 1.14.1, Apple Accelerate\n\n| N | DOFs | FWD Time | BWD Time | Peak RAM |\n| --- | -------- | --------- | --------- | ---------- |\n| 10 | 3000 | 0.14s | 0.03s | 592.2MB |\n| 20 | 24000 | 0.99s | 0.15s | 968.3MB |\n| 30 | 81000 | 3.42s | 0.57s | 1562.8MB |\n| 40 | 192000 | 8.48s | 1.14s | 2497.1MB |\n| 50 | 375000 | 16.46s | 2.23s | 3963.7MB |\n| 60 | 648000 | 28.63s | 3.56s | 5503.3MB |\n| 70 | 1029000 | 46.86s | 5.91s | 6309.5MB |\n| 80 | 1536000 | 74.12s | 10.69s | 6933.7MB |\n| 90 | 2187000 | 121.11s | 16.63s | 7663.5MB |\n| 100 | 3000000 | 179.44s | 38.35s | 9662.4MB |\n\n\n#### AMD Ryzen Threadripper PRO 5995WX (64 Cores, 512 GB RAM) and NVIDIA GeForce RTX 4090\nPython 3.12, CuPy 13.3.0, CUDA 11.8\n\n| N | DOFs | FWD Time | BWD Time | Peak RAM |\n| --- | -------- | --------- | --------- | ---------- |\n| 10 | 3000 | 0.66s | 0.15s | 1371.7MB |\n| 20 | 24000 | 1.00s | 0.43s | 1358.9MB |\n| 30 | 81000 | 1.14s | 0.65s | 1371.1MB |\n| 40 | 192000 | 1.37s | 0.83s | 1367.3MB |\n| 50 | 375000 | 1.51s | 1.04s | 1356.4MB |\n| 60 | 648000 | 1.94s | 1.43s | 1342.1MB |\n| 70 | 1029000 | 5.19s | 4.31s | 1366.8MB |\n| 80 | 1536000 | 7.48s | 18.88s | 5105.6MB |\n\n\n",
"bugtrack_url": null,
"license": "Copyright 2024 Nils Meyer\n \n Permission is hereby granted, free of charge, to any person obtaining a copy of this software and associated documentation files (the \u201cSoftware\u201d), to deal in the Software without restriction, including without limitation the rights to use, copy, modify, merge, publish, distribute, sublicense, and/or sell copies of the Software, and to permit persons to whom the Software is furnished to do so, subject to the following conditions:\n \n The above copyright notice and this permission notice shall be included in all copies or substantial portions of the Software.\n \n THE SOFTWARE IS PROVIDED \u201cAS IS\u201d, WITHOUT WARRANTY OF ANY KIND, EXPRESS OR IMPLIED, INCLUDING BUT NOT LIMITED TO THE WARRANTIES OF MERCHANTABILITY, FITNESS FOR A PARTICULAR PURPOSE AND NONINFRINGEMENT. IN NO EVENT SHALL THE AUTHORS OR COPYRIGHT HOLDERS BE LIABLE FOR ANY CLAIM, DAMAGES OR OTHER LIABILITY, WHETHER IN AN ACTION OF CONTRACT, TORT OR OTHERWISE, ARISING FROM, OUT OF OR IN CONNECTION WITH THE SOFTWARE OR THE USE OR OTHER DEALINGS IN THE SOFTWARE.",
"summary": "GPU accelerated differential finite elements for solid mechanics with PyTorch.",
"version": "0.3.8",
"project_urls": {
"source": "https://github.com/meyer-nils/torch-fem"
},
"split_keywords": [
"finite elements",
" automatic differentiation"
],
"urls": [
{
"comment_text": null,
"digests": {
"blake2b_256": "fab11860727e15a6c5564b6c6b099fa7ad277f1631007cd09d6ca4faadbf8694",
"md5": "c6f95d318d96e1d43a68bfe5b7fd03dc",
"sha256": "1d36af9b77ad3e928af0cc8fb441a7cb5105835caf5e6b3574ae46b6459ae566"
},
"downloads": -1,
"filename": "torch_fem-0.3.8-py3-none-any.whl",
"has_sig": false,
"md5_digest": "c6f95d318d96e1d43a68bfe5b7fd03dc",
"packagetype": "bdist_wheel",
"python_version": "py3",
"requires_python": ">=3.10",
"size": 2700301,
"upload_time": "2025-02-10T08:03:27",
"upload_time_iso_8601": "2025-02-10T08:03:27.499269Z",
"url": "https://files.pythonhosted.org/packages/fa/b1/1860727e15a6c5564b6c6b099fa7ad277f1631007cd09d6ca4faadbf8694/torch_fem-0.3.8-py3-none-any.whl",
"yanked": false,
"yanked_reason": null
},
{
"comment_text": null,
"digests": {
"blake2b_256": "4c5605cface4b425d2a90f505a2698118928c8083913883d4db056f62ddea1a7",
"md5": "0811e825973f0db7bbd22a3ed70cb2f3",
"sha256": "b7d076123b27c544e0338516defd10098a33d8fa0a77db9a61db47af71630438"
},
"downloads": -1,
"filename": "torch_fem-0.3.8.tar.gz",
"has_sig": false,
"md5_digest": "0811e825973f0db7bbd22a3ed70cb2f3",
"packagetype": "sdist",
"python_version": "source",
"requires_python": ">=3.10",
"size": 2699029,
"upload_time": "2025-02-10T08:03:30",
"upload_time_iso_8601": "2025-02-10T08:03:30.081174Z",
"url": "https://files.pythonhosted.org/packages/4c/56/05cface4b425d2a90f505a2698118928c8083913883d4db056f62ddea1a7/torch_fem-0.3.8.tar.gz",
"yanked": false,
"yanked_reason": null
}
],
"upload_time": "2025-02-10 08:03:30",
"github": true,
"gitlab": false,
"bitbucket": false,
"codeberg": false,
"github_user": "meyer-nils",
"github_project": "torch-fem",
"travis_ci": false,
"coveralls": false,
"github_actions": true,
"lcname": "torch-fem"
}
