# $\Phi$-SO : Physical Symbolic Optimization

Physical symbolic optimization ( $\Phi$-SO ) - A symbolic optimization package built for physics.
[](https://github.com/WassimTenachi/PhySO)
[](https://physo.readthedocs.io/en/latest/?badge=latest)
[](https://coveralls.io/github/WassimTenachi/PhySO?branch=main)
[](https://twitter.com/WassimTenachi)
[](https://arxiv.org/abs/2303.03192)
[](https://arxiv.org/abs/2312.01816)
[](https://badge.fury.io/py/physo)
[](https://anaconda.org/conda-forge/physo)
Source code: [WassimTenachi/PhySO](https://github.com/WassimTenachi/PhySO)\
Documentation: [physo.readthedocs.io](https://physo.readthedocs.io/en/latest/)
## What's New ✨
**2025-08** : 📦 Install via `pip install physo` and `conda` now available!
**2025-07** : 🐍 Python 3.12 + latest `NumPy`/`PyTorch`/`SymPy` support.
**2024-06** : 📚 Full documentation overhaul.
**2024-05** : 🔬 **Class SR**: Multi-dataset symbolic regression.
**2024-02** : 🎯 Uncertainty-aware fitting.
**2023-08** : ⚡ Dimensional analysis acceleration.
**2023-03** : 🌟 **PhySO** initial release (physics-focused SR).
## Highlights
$\Phi$-SO's symbolic regression module uses deep reinforcement learning to infer analytical physical laws that fit data points, searching in the space of functional forms.
`physo` is able to leverage:
* Physical units constraints, reducing the search space with dimensional analysis ([[Tenachi et al 2023]](https://arxiv.org/abs/2303.03192))
* Class constraints, searching for a single analytical functional form that accurately fits multiple datasets - each governed by its own (possibly) unique set of fitting parameters ([[Tenachi et al 2024]](https://arxiv.org/abs/2312.01816))
$\Phi$-SO recovering the equation for a damped harmonic oscillator:
https://github.com/WassimTenachi/PhySO/assets/63928316/655b0eea-70ba-4975-8a80-00553a6e2786
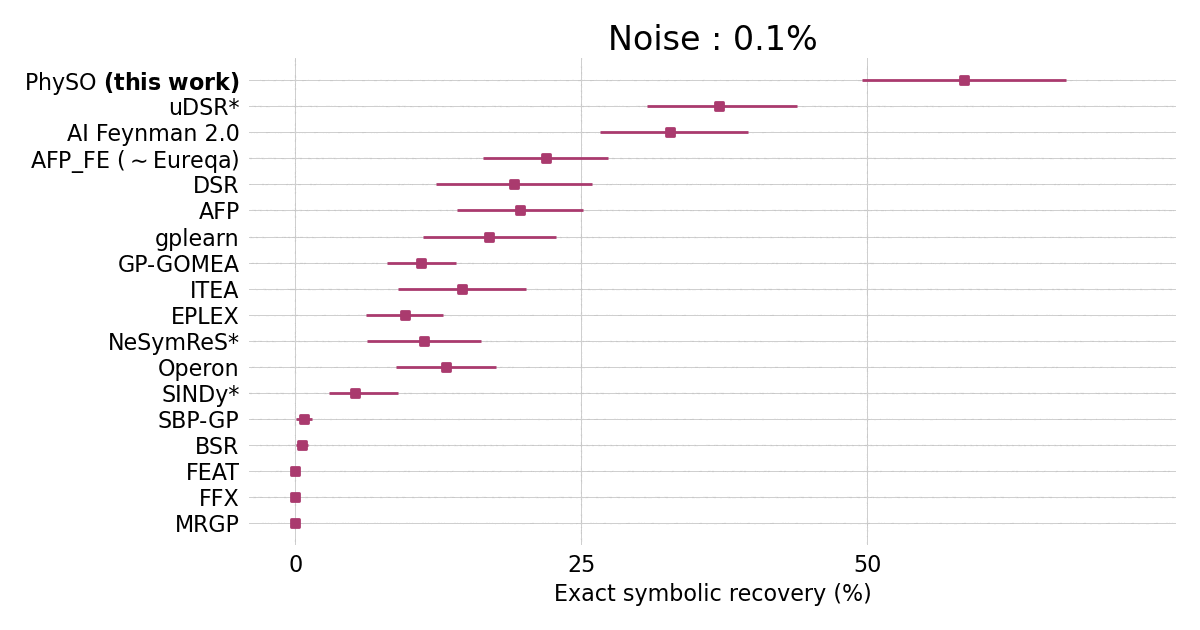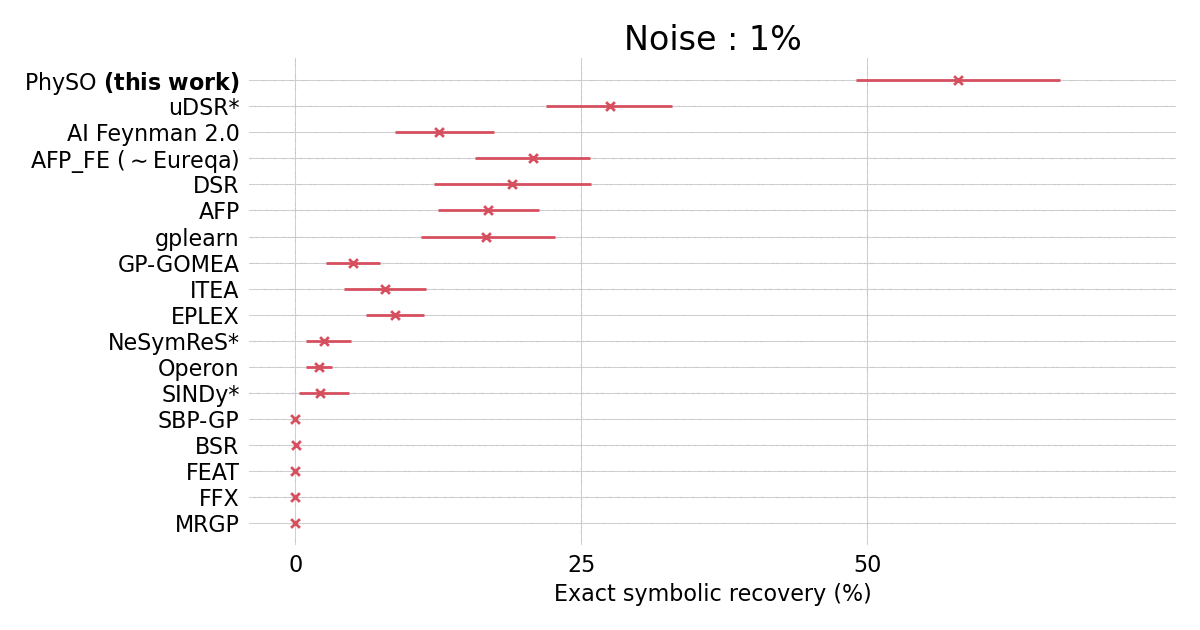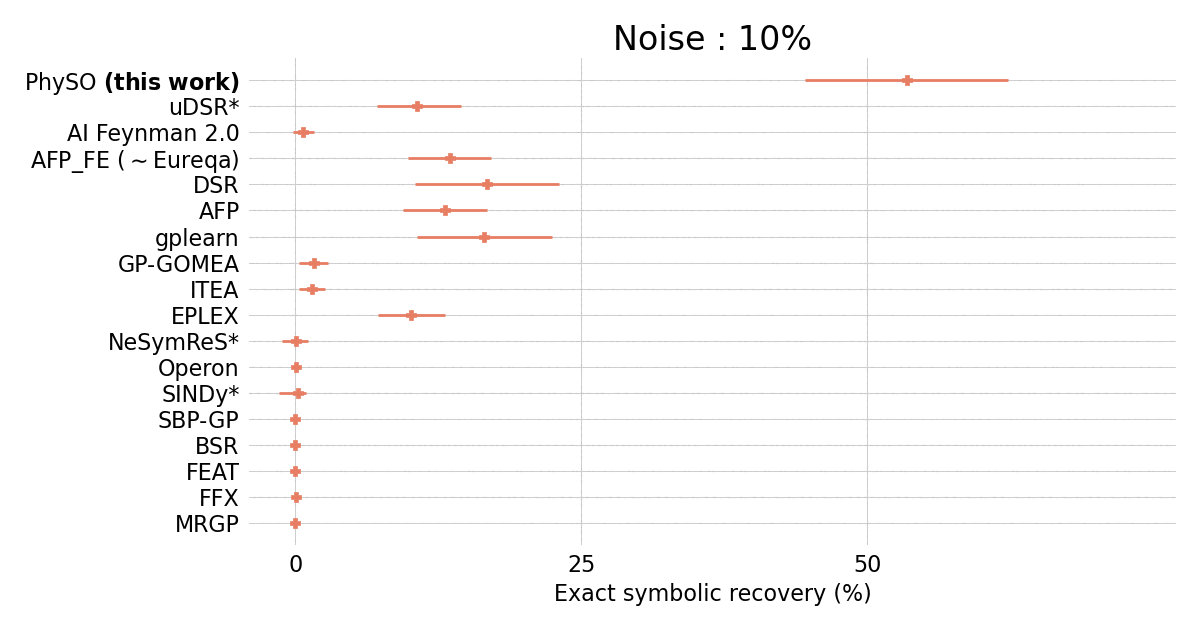
Performances on the standard Feynman benchmark from [SRBench](https://github.com/cavalab/srbench/tree/master)) comprising 120 expressions from the Feynman Lectures on Physics against popular SR packages.
$\Phi$-SO achieves state-of-the-art performance in the presence of noise (exceeding 0.1%) and shows robust performances even in the presence of substantial (10%) noise:
# Installation
The package has been tested on:
- Linux
- OSX (ARM & Intel)
- Windows
If you are encountering issues with the installation, [installing from the source](https://physo.readthedocs.io/en/latest/r_installation.html#source-install) should help.
If you are still having issues, please refer to the [FAQ](https://physo.readthedocs.io/en/latest/r_faq.html) or raise an issue on the [GitHub repository](https://github.com/WassimTenachi/PhySO/issues).
## Installing with pip
Installing `physo` from PyPI :
```bash
pip install physo
```
## Installing with conda
Installing `physo` using conda:
```bash
conda install -c conda-forge physo
```
## Getting started (SR)
In this tutorial, we show how to use `physo` to perform Symbolic Regression (SR).
The reference notebook for this tutorial can be found here: [sr_quick_start.ipynb](https://github.com/WassimTenachi/PhySO/blob/main/demos/sr_quick_start.ipynb).
### Setup
Importing the necessary libraries:
```
# External packages
import numpy as np
import matplotlib.pyplot as plt
import torch
```
Importing `physo`:
```
# Internal code import
import physo
import physo.learn.monitoring as monitoring
```
It is recommended to fix the seed for reproducibility:
```
# Seed
seed = 0
np.random.seed(seed)
torch.manual_seed(seed)
```
### Making synthetic datasets
Making a toy synthetic dataset:
```
# Making toy synthetic data
z = np.random.uniform(-10, 10, 50)
v = np.random.uniform(-10, 10, 50)
X = np.stack((z, v), axis=0)
y = 1.234*9.807*z + 1.234*v**2
```
It should be noted that free constants search starts around 1. by default. Therefore when using default hyperparameters, normalizing the data around an order of magnitude of 1 is strongly recommended.
---
__DA side notes__:
$\Phi$-SO can exploit DA (dimensional analysis) to make SR more efficient.
On can consider the physical units of $X=(z,v)$, $z$ being a length of dimension $L^{1}, T^{0}, M^{0}$, v a velocity of dimension $L^{1}, T^{-1}, M^{0}$, $y=E$ if an energy of dimension $L^{2}, T^{-2}, M^{1}$.
If you are not working on a physics problem and all your variables/constants are dimensionless, do not specify any of the `xx_units` arguments (or specify them as `[0,0]` for all variables/constants) and `physo` will perform a dimensionless symbolic regression task.
---
Datasets plot:
```
n_dim = X.shape[0]
fig, ax = plt.subplots(n_dim, 1, figsize=(10,5))
for i in range (n_dim):
curr_ax = ax if n_dim==1 else ax[i]
curr_ax.plot(X[i], y, 'k.',)
curr_ax.set_xlabel("X[%i]"%(i))
curr_ax.set_ylabel("y")
plt.show()
```
### SR configuration
It should be noted that SR capabilities of `physo` are heavily dependent on hyperparameters, it is therefore recommended to tune hyperparameters to your own specific problem for doing science.
Summary of currently available hyperparameters presets configurations:
| Config | Recommended usecases | Speed | Effectiveness | Notes |
|:----------:|:---------------------------------------------------------:|:-----------:|:-----------------:|:--------------------------------------------------------------:|
| `config0` | Demos | ★★★ | ★ | Light and fast config. |
| `config1` | SR with DA $^*$ ; Class SR with DA $^*$ | ★ | ★★★ | Config used for Feynman Benchmark and MW streams Benchmark. |
| `config2` | SR ; Class SR | ★★ | ★★ | Config used for Class Benchmark. |
$^*$ DA = Dimensional Analysis
Users are encouraged to edit configurations (they can be found in: [physo/config/](https://github.com/WassimTenachi/PhySO/tree/main/physo/config)).
By default, `config0` is used, however it is recommended to follow the upper recommendations for doing science.
---
__DA side notes__:
1. During the first tens of iterations, the neural network is typically still learning the rules of dimensional analysis, resulting in most candidates being discarded and not learned on, effectively resulting in a much smaller batch size (typically 10x smaller), thus making the evaluation process much less computationally expensive. It is therefore recommended to compensate this behavior by using a higher batch size configuration which helps provide the neural network sufficient learning information.
---
Logging and visualisation setup:
```
save_path_training_curves = 'demo_curves.png'
save_path_log = 'demo.log'
run_logger = lambda : monitoring.RunLogger(save_path = save_path_log,
do_save = True)
run_visualiser = lambda : monitoring.RunVisualiser (epoch_refresh_rate = 1,
save_path = save_path_training_curves,
do_show = False,
do_prints = True,
do_save = True, )
```
### Running SR
Given variables data $(x_0,..., x_n)$ (here $(z, v)$ ), the root variable $y$ (here $E$) as well as free and fixed constants, you can run an SR task to recover $f$ via the following command.
---
__DA side notes__:
Here we are allowing the use of a fixed constant $1$ of dimension $L^{0}, T^{0}, M^{0}$ (ie dimensionless) and free constants $m$ of dimension $L^{0}, T^{0}, M^{1}$ and $g$ of dimension $L^{1}, T^{-2}, M^{0}$.
It should be noted that here the units vector are of size 3 (eg: `[1, 0, 0]`) as in this example the variables have units dependent on length, time and mass only.
However, units vectors can be of any size $\leq 7$ as long as it is consistent across X, y and constants, allowing the user to express any units (dependent on length, time, mass, temperature, electric current, amount of light, or amount of matter).
In addition, dimensional analysis can be performed regardless of the order in which units are given, allowing the user to use any convention ([length, mass, time] or [mass, time, length] etc.) as long as it is consistent across X,y and constants.
---
```
# Running SR task
expression, logs = physo.SR(X, y,
# Giving names of variables (for display purposes)
X_names = [ "z" , "v" ],
# Associated physical units (ignore or pass zeroes if irrelevant)
X_units = [ [1, 0, 0] , [1, -1, 0] ],
# Giving name of root variable (for display purposes)
y_name = "E",
y_units = [2, -2, 1],
# Fixed constants
fixed_consts = [ 1. ],
fixed_consts_units = [ [0,0,0] ],
# Free constants names (for display purposes)
free_consts_names = [ "m" , "g" ],
free_consts_units = [ [0, 0, 1] , [1, -2, 0] ],
# Symbolic operations that can be used to make f
op_names = ["mul", "add", "sub", "div", "inv", "n2", "sqrt", "neg", "exp", "log", "sin", "cos"],
get_run_logger = run_logger,
get_run_visualiser = run_visualiser,
# Run config
run_config = physo.config.config0.config0,
# Parallel mode (only available when running from python scripts, not notebooks)
parallel_mode = False,
# Number of iterations
epochs = 20
)
```
### Inspecting the best expression found
__Getting best expression:__
The best expression found (in accuracy) is returned in the `expression` variable:
```
best_expr = expression
print(best_expr.get_infix_pretty())
```
```
>>>
2
-g⋅m⋅z + -v⋅v⋅sin (1.0)⋅1.0⋅m
```
It can also be loaded later on from log files:
```
import physo
from physo.benchmark.utils import symbolic_utils as su
import sympy
# Loading pareto front expressions
pareto_expressions = physo.read_pareto_pkl("demo_curves_pareto.pkl")
# Most accurate expression is the last in the Pareto front:
best_expr = pareto_expressions[-1]
print(best_expr.get_infix_pretty())
```
__Display:__
The expression can be converted into...
A sympy expression:
```
best_expr.get_infix_sympy()
```
```
>>> -g*m*z - v*v*sin(1.0)**2*1.0*m
```
A sympy expression (with evaluated free constants values):
```
best_expr.get_infix_sympy(evaluate_consts=True)[0]
```
```
>>> 1.74275713004454*v**2*sin(1.0)**2 + 12.1018380702846*z
```
A latex string:
```
best_expr.get_infix_latex()
```
```
>>> '\\frac{m \\left(- 1000000000000000 g z - 708073418273571 v^{2}\\right)}{1000000000000000}'
```
A latex string (with evaluated free constants values):
```
sympy.latex(best_expr.get_infix_sympy(evaluate_consts=True))
```
```
>>> '\\mathtt{\\text{[1.74275713004454*v**2*sin(1.0)**2 + 12.1018380702846*z]}}'
```
__Getting free constant values:__
```
best_expr.free_consts
```
```
>>> FreeConstantsTable
-> Class consts (['g' 'm']) : (1, 2)
-> Spe consts ([]) : (1, 0, 1)
```
```
best_expr.free_consts.class_values
```
```
>>> tensor([[ 6.9441, -1.7428]], dtype=torch.float64)
```
### Checking exact symbolic recovery
```
# To sympy
best_expr = best_expr.get_infix_sympy(evaluate_consts=True)
best_expr = best_expr[0]
# Printing best expression simplified and with rounded constants
print("best_expr : ", su.clean_sympy_expr(best_expr, round_decimal = 4))
# Target expression was:
target_expr = sympy.parse_expr("1.234*9.807*z + 1.234*v**2")
print("target_expr : ", su.clean_sympy_expr(target_expr, round_decimal = 4))
# Check equivalence
print("\nChecking equivalence:")
is_equivalent, log = su.compare_expression(
trial_expr = best_expr,
target_expr = target_expr,
handle_trigo = True,
prevent_zero_frac = True,
prevent_inf_equivalence = True,
verbose = True,
)
print("Is equivalent:", is_equivalent)
```
```
>>> best_expr : 1.234*v**2 + 12.1018*z
target_expr : 1.234*v**2 + 12.1018*z
Checking equivalence:
-> Assessing if 1.234*v**2 + 12.101838*z (target) is equivalent to 1.74275713004454*v**2*sin(1.0)**2 + 12.1018380702846*z (trial)
-> Simplified expression : 1.23*v**2 + 12.1*z
-> Symbolic error : 0
-> Symbolic fraction : 1
-> Trigo symbolic error : 0
-> Trigo symbolic fraction : 1
-> Equivalent : True
Is equivalent: True
```
# Documentation
Further documentation can be found at [physo.readthedocs.io](https://physo.readthedocs.io/en/latest/).
Quick start guide for __Symbolic Regression__ : [HERE](https://physo.readthedocs.io/en/latest/r_sr.html#getting-started-sr)
Quick start guide for __Class Symbolic Regression__ : [HERE](https://physo.readthedocs.io/en/latest/r_class_sr.html#getting-started-class-sr)
# Citing this work
Symbolic Regression with reinforcement learning & dimensional analysis
```
@ARTICLE{PhySO_RL_DA,
author = {{Tenachi}, Wassim and {Ibata}, Rodrigo and {Diakogiannis}, Foivos I.},
title = "{Deep Symbolic Regression for Physics Guided by Units Constraints: Toward the Automated Discovery of Physical Laws}",
journal = {ApJ},
year = 2023,
month = dec,
volume = {959},
number = {2},
eid = {99},
pages = {99},
doi = {10.3847/1538-4357/ad014c},
archivePrefix = {arXiv},
eprint = {2303.03192},
primaryClass = {astro-ph.IM},
adsurl = {https://ui.adsabs.harvard.edu/abs/2023ApJ...959...99T},
adsnote = {Provided by the SAO/NASA Astrophysics Data System}
}
```
Class Symbolic Regression
```
@ARTICLE{PhySO_ClassSR,
author = {{Tenachi}, Wassim and {Ibata}, Rodrigo and {Fran{\c{c}}ois}, Thibaut L. and {Diakogiannis}, Foivos I.},
title = "{Class Symbolic Regression: Gotta Fit 'Em All}",
journal = {The Astrophysical Journal Letters},
year = {2024},
month = {jul},
volume = {969},
number = {2},
eid = {arXiv:2312.01816},
pages = {L26},
doi = {10.3847/2041-8213/ad5970},
archivePrefix = {arXiv},
eprint = {2312.01816},
primaryClass = {cs.LG},
adsurl = {https://ui.adsabs.harvard.edu/abs/2023arXiv231201816T},
adsnote = {Provided by the SAO/NASA Astrophysics Data System}
}
```
Raw data
{
"_id": null,
"home_page": "https://github.com/WassimTenachi/PhySO",
"name": "physo",
"maintainer": null,
"docs_url": null,
"requires_python": ">=3.8",
"maintainer_email": null,
"keywords": "physical symbolic optimization, symbolic optimization, machine learning, reinforcement learning, deep learning, physics, symbolic regression, equation discovery",
"author": "Wassim Tenachi",
"author_email": "w.tenachi@gmail.com",
"download_url": "https://files.pythonhosted.org/packages/bc/59/a48b72caadc82b6f6ab7fb5d69b244f3cb08f52048e44e7de4f75e348f4e/physo-1.1.11.tar.gz",
"platform": null,
"description": "# $\\Phi$-SO : Physical Symbolic Optimization\n\nPhysical symbolic optimization ( $\\Phi$-SO ) - A symbolic optimization package built for physics.\n\n[](https://github.com/WassimTenachi/PhySO)\n[](https://physo.readthedocs.io/en/latest/?badge=latest)\n[](https://coveralls.io/github/WassimTenachi/PhySO?branch=main)\n[](https://twitter.com/WassimTenachi)\n[](https://arxiv.org/abs/2303.03192)\n[](https://arxiv.org/abs/2312.01816)\n\n[](https://badge.fury.io/py/physo)\n[](https://anaconda.org/conda-forge/physo)\n\n\nSource code: [WassimTenachi/PhySO](https://github.com/WassimTenachi/PhySO)\\\nDocumentation: [physo.readthedocs.io](https://physo.readthedocs.io/en/latest/)\n\n## What's New \u2728 \n\n**2025-08** : \ud83d\udce6 Install via `pip install physo` and `conda` now available! \n**2025-07** : \ud83d\udc0d Python 3.12 + latest `NumPy`/`PyTorch`/`SymPy` support. \n**2024-06** : \ud83d\udcda Full documentation overhaul. \n**2024-05** : \ud83d\udd2c **Class SR**: Multi-dataset symbolic regression. \n**2024-02** : \ud83c\udfaf Uncertainty-aware fitting. \n**2023-08** : \u26a1 Dimensional analysis acceleration. \n**2023-03** : \ud83c\udf1f **PhySO** initial release (physics-focused SR).\n\n## Highlights\n\n$\\Phi$-SO's symbolic regression module uses deep reinforcement learning to infer analytical physical laws that fit data points, searching in the space of functional forms. \n\n`physo` is able to leverage:\n\n* Physical units constraints, reducing the search space with dimensional analysis ([[Tenachi et al 2023]](https://arxiv.org/abs/2303.03192))\n\n* Class constraints, searching for a single analytical functional form that accurately fits multiple datasets - each governed by its own (possibly) unique set of fitting parameters ([[Tenachi et al 2024]](https://arxiv.org/abs/2312.01816))\n\n$\\Phi$-SO recovering the equation for a damped harmonic oscillator:\n\nhttps://github.com/WassimTenachi/PhySO/assets/63928316/655b0eea-70ba-4975-8a80-00553a6e2786\n\nPerformances on the standard Feynman benchmark from [SRBench](https://github.com/cavalab/srbench/tree/master)) comprising 120 expressions from the Feynman Lectures on Physics against popular SR packages.\n\n$\\Phi$-SO achieves state-of-the-art performance in the presence of noise (exceeding 0.1%) and shows robust performances even in the presence of substantial (10%) noise:\n\n\n\n# Installation\n\nThe package has been tested on:\n- Linux\n- OSX (ARM & Intel)\n- Windows\n\nIf you are encountering issues with the installation, [installing from the source](https://physo.readthedocs.io/en/latest/r_installation.html#source-install) should help.\nIf you are still having issues, please refer to the [FAQ](https://physo.readthedocs.io/en/latest/r_faq.html) or raise an issue on the [GitHub repository](https://github.com/WassimTenachi/PhySO/issues).\n\n## Installing with pip\n\nInstalling `physo` from PyPI :\n```bash\npip install physo\n```\n\n## Installing with conda\n\nInstalling `physo` using conda:\n```bash\nconda install -c conda-forge physo\n```\n## Getting started (SR)\n\nIn this tutorial, we show how to use `physo` to perform Symbolic Regression (SR).\nThe reference notebook for this tutorial can be found here: [sr_quick_start.ipynb](https://github.com/WassimTenachi/PhySO/blob/main/demos/sr_quick_start.ipynb).\n\n### Setup\n\nImporting the necessary libraries:\n```\n# External packages\nimport numpy as np\nimport matplotlib.pyplot as plt\nimport torch\n```\n\nImporting `physo`:\n```\n# Internal code import\nimport physo\nimport physo.learn.monitoring as monitoring\n```\n\nIt is recommended to fix the seed for reproducibility:\n```\n# Seed\nseed = 0\nnp.random.seed(seed)\ntorch.manual_seed(seed)\n```\n\n### Making synthetic datasets\n\nMaking a toy synthetic dataset:\n```\n# Making toy synthetic data\nz = np.random.uniform(-10, 10, 50)\nv = np.random.uniform(-10, 10, 50)\nX = np.stack((z, v), axis=0)\ny = 1.234*9.807*z + 1.234*v**2\n```\nIt should be noted that free constants search starts around 1. by default. Therefore when using default hyperparameters, normalizing the data around an order of magnitude of 1 is strongly recommended.\n\n---\n\n__DA side notes__: \n$\\Phi$-SO can exploit DA (dimensional analysis) to make SR more efficient. \nOn can consider the physical units of $X=(z,v)$, $z$ being a length of dimension $L^{1}, T^{0}, M^{0}$, v a velocity of dimension $L^{1}, T^{-1}, M^{0}$, $y=E$ if an energy of dimension $L^{2}, T^{-2}, M^{1}$.\nIf you are not working on a physics problem and all your variables/constants are dimensionless, do not specify any of the `xx_units` arguments (or specify them as `[0,0]` for all variables/constants) and `physo` will perform a dimensionless symbolic regression task. \n\n---\n\nDatasets plot:\n```\nn_dim = X.shape[0]\nfig, ax = plt.subplots(n_dim, 1, figsize=(10,5))\nfor i in range (n_dim):\n curr_ax = ax if n_dim==1 else ax[i]\n curr_ax.plot(X[i], y, 'k.',)\n curr_ax.set_xlabel(\"X[%i]\"%(i))\n curr_ax.set_ylabel(\"y\")\nplt.show()\n```\n\n### SR configuration\n\nIt should be noted that SR capabilities of `physo` are heavily dependent on hyperparameters, it is therefore recommended to tune hyperparameters to your own specific problem for doing science. \nSummary of currently available hyperparameters presets configurations:\n\n| Config | Recommended usecases | Speed | Effectiveness | Notes |\n|:----------:|:---------------------------------------------------------:|:-----------:|:-----------------:|:--------------------------------------------------------------:|\n| `config0` | Demos | \u2605\u2605\u2605 | \u2605 | Light and fast config. |\n| `config1` | SR with DA $^*$ ; Class SR with DA $^*$ | \u2605 | \u2605\u2605\u2605 | Config used for Feynman Benchmark and MW streams Benchmark. |\n| `config2` | SR ; Class SR | \u2605\u2605 | \u2605\u2605 | Config used for Class Benchmark. |\n\n$^*$ DA = Dimensional Analysis\n\nUsers are encouraged to edit configurations (they can be found in: [physo/config/](https://github.com/WassimTenachi/PhySO/tree/main/physo/config)). \nBy default, `config0` is used, however it is recommended to follow the upper recommendations for doing science.\n\n---\n__DA side notes__: \n1. During the first tens of iterations, the neural network is typically still learning the rules of dimensional analysis, resulting in most candidates being discarded and not learned on, effectively resulting in a much smaller batch size (typically 10x smaller), thus making the evaluation process much less computationally expensive. It is therefore recommended to compensate this behavior by using a higher batch size configuration which helps provide the neural network sufficient learning information. \n---\n\nLogging and visualisation setup:\n```\nsave_path_training_curves = 'demo_curves.png'\nsave_path_log = 'demo.log'\n\nrun_logger = lambda : monitoring.RunLogger(save_path = save_path_log,\n do_save = True)\n\nrun_visualiser = lambda : monitoring.RunVisualiser (epoch_refresh_rate = 1,\n save_path = save_path_training_curves,\n do_show = False,\n do_prints = True,\n do_save = True, )\n```\n\n### Running SR\n\nGiven variables data $(x_0,..., x_n)$ (here $(z, v)$ ), the root variable $y$ (here $E$) as well as free and fixed constants, you can run an SR task to recover $f$ via the following command.\n\n---\n\n__DA side notes__: \nHere we are allowing the use of a fixed constant $1$ of dimension $L^{0}, T^{0}, M^{0}$ (ie dimensionless) and free constants $m$ of dimension $L^{0}, T^{0}, M^{1}$ and $g$ of dimension $L^{1}, T^{-2}, M^{0}$. \nIt should be noted that here the units vector are of size 3 (eg: `[1, 0, 0]`) as in this example the variables have units dependent on length, time and mass only.\nHowever, units vectors can be of any size $\\leq 7$ as long as it is consistent across X, y and constants, allowing the user to express any units (dependent on length, time, mass, temperature, electric current, amount of light, or amount of matter). \nIn addition, dimensional analysis can be performed regardless of the order in which units are given, allowing the user to use any convention ([length, mass, time] or [mass, time, length] etc.) as long as it is consistent across X,y and constants. \n\n---\n\n```\n# Running SR task\nexpression, logs = physo.SR(X, y,\n # Giving names of variables (for display purposes)\n X_names = [ \"z\" , \"v\" ],\n # Associated physical units (ignore or pass zeroes if irrelevant)\n X_units = [ [1, 0, 0] , [1, -1, 0] ],\n # Giving name of root variable (for display purposes)\n y_name = \"E\",\n y_units = [2, -2, 1],\n # Fixed constants\n fixed_consts = [ 1. ],\n fixed_consts_units = [ [0,0,0] ],\n # Free constants names (for display purposes)\n free_consts_names = [ \"m\" , \"g\" ],\n free_consts_units = [ [0, 0, 1] , [1, -2, 0] ],\n # Symbolic operations that can be used to make f\n op_names = [\"mul\", \"add\", \"sub\", \"div\", \"inv\", \"n2\", \"sqrt\", \"neg\", \"exp\", \"log\", \"sin\", \"cos\"],\n get_run_logger = run_logger,\n get_run_visualiser = run_visualiser,\n # Run config\n run_config = physo.config.config0.config0,\n # Parallel mode (only available when running from python scripts, not notebooks)\n parallel_mode = False,\n # Number of iterations\n epochs = 20\n)\n```\n\n### Inspecting the best expression found\n\n__Getting best expression:__\n\nThe best expression found (in accuracy) is returned in the `expression` variable:\n```\nbest_expr = expression\nprint(best_expr.get_infix_pretty())\n```\n```\n>>> \n 2 \n -g\u22c5m\u22c5z + -v\u22c5v\u22c5sin (1.0)\u22c51.0\u22c5m\n```\n\nIt can also be loaded later on from log files:\n```\nimport physo\nfrom physo.benchmark.utils import symbolic_utils as su\nimport sympy\n\n# Loading pareto front expressions\npareto_expressions = physo.read_pareto_pkl(\"demo_curves_pareto.pkl\")\n# Most accurate expression is the last in the Pareto front:\nbest_expr = pareto_expressions[-1]\nprint(best_expr.get_infix_pretty())\n```\n\n__Display:__\n\nThe expression can be converted into... \nA sympy expression:\n\n```\nbest_expr.get_infix_sympy()\n```\n```\n>>> -g*m*z - v*v*sin(1.0)**2*1.0*m\n```\n\nA sympy expression (with evaluated free constants values):\n\n```\nbest_expr.get_infix_sympy(evaluate_consts=True)[0]\n```\n\n```\n>>> 1.74275713004454*v**2*sin(1.0)**2 + 12.1018380702846*z\n```\n\nA latex string:\n\n```\nbest_expr.get_infix_latex()\n```\n\n```\n>>> '\\\\frac{m \\\\left(- 1000000000000000 g z - 708073418273571 v^{2}\\\\right)}{1000000000000000}'\n```\n\nA latex string (with evaluated free constants values):\n```\nsympy.latex(best_expr.get_infix_sympy(evaluate_consts=True))\n```\n\n```\n>>> '\\\\mathtt{\\\\text{[1.74275713004454*v**2*sin(1.0)**2 + 12.1018380702846*z]}}'\n```\n\n__Getting free constant values:__\n\n```\nbest_expr.free_consts\n```\n```\n>>> FreeConstantsTable\n -> Class consts (['g' 'm']) : (1, 2)\n -> Spe consts ([]) : (1, 0, 1)\n```\n\n```\nbest_expr.free_consts.class_values\n```\n```\n>>> tensor([[ 6.9441, -1.7428]], dtype=torch.float64)\n```\n\n### Checking exact symbolic recovery\n\n```\n# To sympy\nbest_expr = best_expr.get_infix_sympy(evaluate_consts=True)\n\nbest_expr = best_expr[0]\n\n# Printing best expression simplified and with rounded constants\nprint(\"best_expr : \", su.clean_sympy_expr(best_expr, round_decimal = 4))\n\n# Target expression was:\ntarget_expr = sympy.parse_expr(\"1.234*9.807*z + 1.234*v**2\")\nprint(\"target_expr : \", su.clean_sympy_expr(target_expr, round_decimal = 4))\n\n# Check equivalence\nprint(\"\\nChecking equivalence:\")\nis_equivalent, log = su.compare_expression(\n trial_expr = best_expr,\n target_expr = target_expr,\n handle_trigo = True,\n prevent_zero_frac = True,\n prevent_inf_equivalence = True,\n verbose = True,\n)\nprint(\"Is equivalent:\", is_equivalent)\n```\n\n```\n>>> best_expr : 1.234*v**2 + 12.1018*z\n target_expr : 1.234*v**2 + 12.1018*z\n \n Checking equivalence:\n -> Assessing if 1.234*v**2 + 12.101838*z (target) is equivalent to 1.74275713004454*v**2*sin(1.0)**2 + 12.1018380702846*z (trial)\n -> Simplified expression : 1.23*v**2 + 12.1*z\n -> Symbolic error : 0\n -> Symbolic fraction : 1\n -> Trigo symbolic error : 0\n -> Trigo symbolic fraction : 1\n -> Equivalent : True\n Is equivalent: True\n```\n\n# Documentation\n\nFurther documentation can be found at [physo.readthedocs.io](https://physo.readthedocs.io/en/latest/).\n\nQuick start guide for __Symbolic Regression__ : [HERE](https://physo.readthedocs.io/en/latest/r_sr.html#getting-started-sr) \n\nQuick start guide for __Class Symbolic Regression__ : [HERE](https://physo.readthedocs.io/en/latest/r_class_sr.html#getting-started-class-sr) \n\n# Citing this work\n \nSymbolic Regression with reinforcement learning & dimensional analysis\n\n```\n@ARTICLE{PhySO_RL_DA,\n author = {{Tenachi}, Wassim and {Ibata}, Rodrigo and {Diakogiannis}, Foivos I.},\n title = \"{Deep Symbolic Regression for Physics Guided by Units Constraints: Toward the Automated Discovery of Physical Laws}\",\n journal = {ApJ},\n year = 2023,\n month = dec,\n volume = {959},\n number = {2},\n eid = {99},\n pages = {99},\n doi = {10.3847/1538-4357/ad014c},\narchivePrefix = {arXiv},\n eprint = {2303.03192},\n primaryClass = {astro-ph.IM},\n adsurl = {https://ui.adsabs.harvard.edu/abs/2023ApJ...959...99T},\n adsnote = {Provided by the SAO/NASA Astrophysics Data System}\n}\n```\n\nClass Symbolic Regression\n```\n@ARTICLE{PhySO_ClassSR,\n author = {{Tenachi}, Wassim and {Ibata}, Rodrigo and {Fran{\\c{c}}ois}, Thibaut L. and {Diakogiannis}, Foivos I.},\n title = \"{Class Symbolic Regression: Gotta Fit 'Em All}\",\n journal = {The Astrophysical Journal Letters},\n year = {2024},\n month = {jul},\n volume = {969},\n number = {2},\n eid = {arXiv:2312.01816},\n pages = {L26},\n doi = {10.3847/2041-8213/ad5970},\narchivePrefix = {arXiv},\n eprint = {2312.01816},\n primaryClass = {cs.LG},\n adsurl = {https://ui.adsabs.harvard.edu/abs/2023arXiv231201816T},\n adsnote = {Provided by the SAO/NASA Astrophysics Data System}\n}\n```\n",
"bugtrack_url": null,
"license": "MIT",
"summary": "Physical Symbolic Optimization",
"version": "1.1.11",
"project_urls": {
"Bug Reports": "https://github.com/WassimTenachi/PhySO/issues",
"Documentation": "https://physo.readthedocs.io/",
"Homepage": "https://github.com/WassimTenachi/PhySO",
"Source": "https://github.com/WassimTenachi/PhySO"
},
"split_keywords": [
"physical symbolic optimization",
" symbolic optimization",
" machine learning",
" reinforcement learning",
" deep learning",
" physics",
" symbolic regression",
" equation discovery"
],
"urls": [
{
"comment_text": null,
"digests": {
"blake2b_256": "c31e56106bcb1078cc4863a8ebfc26d5f0c054d76bb98022e0a6e5aa0c8dc56b",
"md5": "54173001880f6b1fbe31b7a3ee186c08",
"sha256": "1deb9e85ac163a9619f3b4ba68743827ddc14b1a51e236092bb99ee1a7c77bff"
},
"downloads": -1,
"filename": "physo-1.1.11-py3-none-any.whl",
"has_sig": false,
"md5_digest": "54173001880f6b1fbe31b7a3ee186c08",
"packagetype": "bdist_wheel",
"python_version": "py3",
"requires_python": ">=3.8",
"size": 235794,
"upload_time": "2025-08-09T08:22:40",
"upload_time_iso_8601": "2025-08-09T08:22:40.111125Z",
"url": "https://files.pythonhosted.org/packages/c3/1e/56106bcb1078cc4863a8ebfc26d5f0c054d76bb98022e0a6e5aa0c8dc56b/physo-1.1.11-py3-none-any.whl",
"yanked": false,
"yanked_reason": null
},
{
"comment_text": null,
"digests": {
"blake2b_256": "bc59a48b72caadc82b6f6ab7fb5d69b244f3cb08f52048e44e7de4f75e348f4e",
"md5": "682222a43846a471857f3122ce179874",
"sha256": "97b656dc74904650790236253fb8ba6c7f56ef02a180acd2801fbb166019fdb4"
},
"downloads": -1,
"filename": "physo-1.1.11.tar.gz",
"has_sig": false,
"md5_digest": "682222a43846a471857f3122ce179874",
"packagetype": "sdist",
"python_version": "source",
"requires_python": ">=3.8",
"size": 205026,
"upload_time": "2025-08-09T08:22:41",
"upload_time_iso_8601": "2025-08-09T08:22:41.946193Z",
"url": "https://files.pythonhosted.org/packages/bc/59/a48b72caadc82b6f6ab7fb5d69b244f3cb08f52048e44e7de4f75e348f4e/physo-1.1.11.tar.gz",
"yanked": false,
"yanked_reason": null
}
],
"upload_time": "2025-08-09 08:22:41",
"github": true,
"gitlab": false,
"bitbucket": false,
"codeberg": false,
"github_user": "WassimTenachi",
"github_project": "PhySO",
"travis_ci": false,
"coveralls": false,
"github_actions": false,
"requirements": [
{
"name": "pytorch",
"specs": [
[
">=",
"1.11.0"
]
]
},
{
"name": "numpy",
"specs": []
},
{
"name": "sympy",
"specs": []
},
{
"name": "pandas",
"specs": []
},
{
"name": "matplotlib",
"specs": []
},
{
"name": "scikit-learn",
"specs": []
}
],
"lcname": "physo"
}
