| Name | pytorch-kinematics JSON |
| Version |
0.7.4
JSON |
| download |
| home_page | None |
| Summary | Robot kinematics implemented in pytorch |
| upload_time | 2024-08-29 23:40:07 |
| maintainer | None |
| docs_url | None |
| author | None |
| requires_python | >=3.6 |
| license | Copyright (c) 2023 University of Michigan ARM Lab Permission is hereby granted, free of charge, to any person obtaining a copy of this software and associated documentation files (the "Software"), to deal in the Software without restriction, including without limitation the rights to use, copy, modify, merge, publish, distribute, sublicense, and/or sell copies of the Software, and to permit persons to whom the Software is furnished to do so, subject to the following conditions: The above copyright notice and this permission notice shall be included in all copies or substantial portions of the Software. THE SOFTWARE IS PROVIDED "AS IS", WITHOUT WARRANTY OF ANY KIND, EXPRESS OR IMPLIED, INCLUDING BUT NOT LIMITED TO THE WARRANTIES OF MERCHANTABILITY, FITNESS FOR A PARTICULAR PURPOSE AND NONINFRINGEMENT. IN NO EVENT SHALL THE AUTHORS OR COPYRIGHT HOLDERS BE LIABLE FOR ANY CLAIM, DAMAGES OR OTHER LIABILITY, WHETHER IN AN ACTION OF CONTRACT, TORT OR OTHERWISE, ARISING FROM, OUT OF OR IN CONNECTION WITH THE SOFTWARE OR THE USE OR OTHER DEALINGS IN THE SOFTWARE. |
| keywords |
kinematics
pytorch
ik
fk
robotics
|
| VCS |
 |
| bugtrack_url |
|
| requirements |
No requirements were recorded.
|
| Travis-CI |
No Travis.
|
| coveralls test coverage |
No coveralls.
|
# PyTorch Robot Kinematics
- Parallel and differentiable forward kinematics (FK), Jacobian calculation, and damped least squares inverse kinematics (IK)
- Load robot description from URDF, SDF, and MJCF formats
- SDF queries batched across configurations and points via [pytorch-volumetric](https://github.com/UM-ARM-Lab/pytorch_volumetric)
# Installation
```shell
pip install pytorch-kinematics
```
For development, clone repository somewhere, then `pip3 install -e .` to install in editable mode.
# Usage
See `tests` for code samples; some are also shown here.
## Reference
[](https://zenodo.org/badge/latestdoi/331721571)
If you use this package in your research, consider citing
```
@software{Zhong_PyTorch_Kinematics_2024,
author = {Zhong, Sheng and Power, Thomas and Gupta, Ashwin and Mitrano, Peter},
doi = {10.5281/zenodo.7700587},
month = feb,
title = {{PyTorch Kinematics}},
version = {v0.7.1},
year = {2024}
}
```
## Forward Kinematics (FK)
```python
import math
import pytorch_kinematics as pk
# load robot description from URDF and specify end effector link
chain = pk.build_serial_chain_from_urdf(open("kuka_iiwa.urdf").read(), "lbr_iiwa_link_7")
# prints out the (nested) tree of links
print(chain)
# prints out list of joint names
print(chain.get_joint_parameter_names())
# specify joint values (can do so in many forms)
th = [0.0, -math.pi / 4.0, 0.0, math.pi / 2.0, 0.0, math.pi / 4.0, 0.0]
# do forward kinematics and get transform objects; end_only=False gives a dictionary of transforms for all links
ret = chain.forward_kinematics(th, end_only=False)
# look up the transform for a specific link
tg = ret['lbr_iiwa_link_7']
# get transform matrix (1,4,4), then convert to separate position and unit quaternion
m = tg.get_matrix()
pos = m[:, :3, 3]
rot = pk.matrix_to_quaternion(m[:, :3, :3])
```
We can parallelize FK by passing in 2D joint values, and also use CUDA if available
```python
import torch
import pytorch_kinematics as pk
d = "cuda" if torch.cuda.is_available() else "cpu"
dtype = torch.float64
chain = pk.build_serial_chain_from_urdf(open("kuka_iiwa.urdf").read(), "lbr_iiwa_link_7")
chain = chain.to(dtype=dtype, device=d)
N = 1000
th_batch = torch.rand(N, len(chain.get_joint_parameter_names()), dtype=dtype, device=d)
# order of magnitudes faster when doing FK in parallel
# elapsed 0.008678913116455078s for N=1000 when parallel
# (N,4,4) transform matrix; only the one for the end effector is returned since end_only=True by default
tg_batch = chain.forward_kinematics(th_batch)
# elapsed 8.44686508178711s for N=1000 when serial
for i in range(N):
tg = chain.forward_kinematics(th_batch[i])
```
We can compute gradients through the FK
```python
import torch
import math
import pytorch_kinematics as pk
chain = pk.build_serial_chain_from_urdf(open("kuka_iiwa.urdf").read(), "lbr_iiwa_link_7")
# require gradient through the input joint values
th = torch.tensor([0.0, -math.pi / 4.0, 0.0, math.pi / 2.0, 0.0, math.pi / 4.0, 0.0], requires_grad=True)
tg = chain.forward_kinematics(th)
m = tg.get_matrix()
pos = m[:, :3, 3]
pos.norm().backward()
# now th.grad is populated
```
We can load SDF and MJCF descriptions too, and pass in joint values via a dictionary (unspecified joints get th=0) for non-serial chains
```python
import math
import torch
import pytorch_kinematics as pk
chain = pk.build_chain_from_sdf(open("simple_arm.sdf").read())
ret = chain.forward_kinematics({'arm_elbow_pan_joint': math.pi / 2.0, 'arm_wrist_lift_joint': -0.5})
# recall that we specify joint values and get link transforms
tg = ret['arm_wrist_roll']
# can also do this in parallel
N = 100
ret = chain.forward_kinematics({'arm_elbow_pan_joint': torch.rand(N, 1), 'arm_wrist_lift_joint': torch.rand(N, 1)})
# (N, 4, 4) transform object
tg = ret['arm_wrist_roll']
# building the robot from a MJCF file
chain = pk.build_chain_from_mjcf(open("ant.xml").read())
print(chain)
print(chain.get_joint_parameter_names())
th = {'hip_1': 1.0, 'ankle_1': 1}
ret = chain.forward_kinematics(th)
chain = pk.build_chain_from_mjcf(open("humanoid.xml").read())
print(chain)
print(chain.get_joint_parameter_names())
th = {'left_knee': 0.0, 'right_knee': 0.0}
ret = chain.forward_kinematics(th)
```
## Jacobian calculation
The Jacobian (in the kinematics context) is a matrix describing how the end effector changes with respect to joint value changes
(where 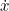 is the twist, or stacked velocity and angular velocity):
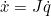
For `SerialChain` we provide a differentiable and parallelizable method for computing the Jacobian with respect to the base frame.
```python
import math
import torch
import pytorch_kinematics as pk
# can convert Chain to SerialChain by choosing end effector frame
chain = pk.build_chain_from_sdf(open("simple_arm.sdf").read())
# print(chain) to see the available links for use as end effector
# note that any link can be chosen; it doesn't have to be a link with no children
chain = pk.SerialChain(chain, "arm_wrist_roll_frame")
chain = pk.build_serial_chain_from_urdf(open("kuka_iiwa.urdf").read(), "lbr_iiwa_link_7")
th = torch.tensor([0.0, -math.pi / 4.0, 0.0, math.pi / 2.0, 0.0, math.pi / 4.0, 0.0])
# (1,6,7) tensor, with 7 corresponding to the DOF of the robot
J = chain.jacobian(th)
# get Jacobian in parallel and use CUDA if available
N = 1000
d = "cuda" if torch.cuda.is_available() else "cpu"
dtype = torch.float64
chain = chain.to(dtype=dtype, device=d)
# Jacobian calculation is differentiable
th = torch.rand(N, 7, dtype=dtype, device=d, requires_grad=True)
# (N,6,7)
J = chain.jacobian(th)
# can get Jacobian at a point offset from the end effector (location is specified in EE link frame)
# by default location is at the origin of the EE frame
loc = torch.rand(N, 3, dtype=dtype, device=d)
J = chain.jacobian(th, locations=loc)
```
The Jacobian can be used to do inverse kinematics. See [IK survey](https://www.math.ucsd.edu/~sbuss/ResearchWeb/ikmethods/iksurvey.pdf)
for a survey of ways to do so. Note that IK may be better performed through other means (but doing it through the Jacobian can give an end-to-end differentiable method).
## Inverse Kinematics (IK)
Inverse kinematics is available via damped least squares (iterative steps with Jacobian pseudo-inverse damped to avoid oscillation near singularlities).
Compared to other IK libraries, these are the typical advantages over them:
- not ROS dependent (many IK libraries need the robot description on the ROS parameter server)
- batched in both goal specification and retries from different starting configurations
- goal orientation in addition to goal position
See `tests/test_inverse_kinematics.py` for usage, but generally what you need is below:
```python
full_urdf = os.path.join(search_path, urdf)
chain = pk.build_serial_chain_from_urdf(open(full_urdf).read(), "lbr_iiwa_link_7")
# goals are specified as Transform3d poses in the **robot frame**
# so if you have the goals specified in the world frame, you also need the robot frame in the world frame
pos = torch.tensor([0.0, 0.0, 0.0], device=device)
rot = torch.tensor([0.0, 0.0, 0.0], device=device)
rob_tf = pk.Transform3d(pos=pos, rot=rot, device=device)
# specify goals as Transform3d poses in world frame
goal_in_world_frame_tf = ...
# convert to robot frame (skip if you have it specified in robot frame already, or if world = robot frame)
goal_in_rob_frame_tf = rob_tf.inverse().compose(goal_tf)
# get robot joint limits
lim = torch.tensor(chain.get_joint_limits(), device=device)
# create the IK object
# see the constructor for more options and their explanations, such as convergence tolerances
ik = pk.PseudoInverseIK(chain, max_iterations=30, num_retries=10,
joint_limits=lim.T,
early_stopping_any_converged=True,
early_stopping_no_improvement="all",
debug=False,
lr=0.2)
# solve IK
sol = ik.solve(goal_in_rob_frame_tf)
# num goals x num retries x DOF tensor of joint angles; if not converged, best solution found so far
print(sol.solutions)
# num goals x num retries can check for the convergence of each run
print(sol.converged)
# num goals x num retries can look at errors directly
print(sol.err_pos)
print(sol.err_rot)
```
## SDF Queries
See [pytorch-volumetric](https://github.com/UM-ARM-Lab/pytorch_volumetric) for the latest details, some instructions are pasted here:
For many applications such as collision checking, it is useful to have the
SDF of a multi-link robot in certain configurations.
First, we create the robot model (loaded from URDF, SDF, MJCF, ...) with
[pytorch kinematics](https://github.com/UM-ARM-Lab/pytorch_kinematics).
For example, we will be using the KUKA 7 DOF arm model from pybullet data
```python
import os
import torch
import pybullet_data
import pytorch_kinematics as pk
import pytorch_volumetric as pv
urdf = "kuka_iiwa/model.urdf"
search_path = pybullet_data.getDataPath()
full_urdf = os.path.join(search_path, urdf)
chain = pk.build_serial_chain_from_urdf(open(full_urdf).read(), "lbr_iiwa_link_7")
d = "cuda" if torch.cuda.is_available() else "cpu"
chain = chain.to(device=d)
# paths to the link meshes are specified with their relative path inside the URDF
# we need to give them the path prefix as we need their absolute path to load
s = pv.RobotSDF(chain, path_prefix=os.path.join(search_path, "kuka_iiwa"))
```
By default, each link will have a `MeshSDF`. To instead use `CachedSDF` for faster queries
```python
s = pv.RobotSDF(chain, path_prefix=os.path.join(search_path, "kuka_iiwa"),
link_sdf_cls=pv.cache_link_sdf_factory(resolution=0.02, padding=1.0, device=d))
```
Which when the `y=0.02` SDF slice is visualized:
With surface points corresponding to:
Queries on this SDF is dependent on the joint configurations (by default all zero).
**Queries are batched across configurations and query points**. For example, we have a batch of
joint configurations to query
```python
th = torch.tensor([0.0, -math.pi / 4.0, 0.0, math.pi / 2.0, 0.0, math.pi / 4.0, 0.0], device=d)
N = 200
th_perturbation = torch.randn(N - 1, 7, device=d) * 0.1
# N x 7 joint values
th = torch.cat((th.view(1, -1), th_perturbation + th))
```
And also a batch of points to query (same points for each configuration):
```python
y = 0.02
query_range = np.array([
[-1, 0.5],
[y, y],
[-0.2, 0.8],
])
# M x 3 points
coords, pts = pv.get_coordinates_and_points_in_grid(0.01, query_range, device=s.device)
```
We set the batch of joint configurations and query:
```python
s.set_joint_configuration(th)
# N x M SDF value
# N x M x 3 SDF gradient
sdf_val, sdf_grad = s(pts)
```
# Credits
- `pytorch_kinematics/transforms` is extracted from [pytorch3d](https://github.com/facebookresearch/pytorch3d) with minor extensions.
This was done instead of including `pytorch3d` as a dependency because it is hard to install and most of its code is unrelated.
An important difference is that we use left hand multiplied transforms as is convention in robotics (T * pt) instead of their
right hand multiplied transforms.
- `pytorch_kinematics/urdf_parser_py`, and `pytorch_kinematics/mjcf_parser` is extracted from [kinpy](https://github.com/neka-nat/kinpy), as well as the FK logic.
This repository ports the logic to pytorch, parallelizes it, and provides some extensions.
Raw data
{
"_id": null,
"home_page": null,
"name": "pytorch-kinematics",
"maintainer": null,
"docs_url": null,
"requires_python": ">=3.6",
"maintainer_email": "Sheng Zhong <zhsh@umich.edu>",
"keywords": "kinematics, pytorch, ik, fk, robotics",
"author": null,
"author_email": "Sheng Zhong <zhsh@umich.edu>",
"download_url": "https://files.pythonhosted.org/packages/27/05/9aae3bed03b6918394961fd0bf4c962676825f2bfca3e883475bdcc0cfd2/pytorch_kinematics-0.7.4.tar.gz",
"platform": null,
"description": "# PyTorch Robot Kinematics\n- Parallel and differentiable forward kinematics (FK), Jacobian calculation, and damped least squares inverse kinematics (IK)\n- Load robot description from URDF, SDF, and MJCF formats \n- SDF queries batched across configurations and points via [pytorch-volumetric](https://github.com/UM-ARM-Lab/pytorch_volumetric)\n\n# Installation\n```shell\npip install pytorch-kinematics\n```\n\nFor development, clone repository somewhere, then `pip3 install -e .` to install in editable mode.\n\n# Usage\n\nSee `tests` for code samples; some are also shown here.\n\n## Reference\n[](https://zenodo.org/badge/latestdoi/331721571)\n\nIf you use this package in your research, consider citing\n```\n@software{Zhong_PyTorch_Kinematics_2024,\nauthor = {Zhong, Sheng and Power, Thomas and Gupta, Ashwin and Mitrano, Peter},\ndoi = {10.5281/zenodo.7700587},\nmonth = feb,\ntitle = {{PyTorch Kinematics}},\nversion = {v0.7.1},\nyear = {2024}\n}\n```\n\n## Forward Kinematics (FK)\n```python\nimport math\nimport pytorch_kinematics as pk\n\n# load robot description from URDF and specify end effector link\nchain = pk.build_serial_chain_from_urdf(open(\"kuka_iiwa.urdf\").read(), \"lbr_iiwa_link_7\")\n# prints out the (nested) tree of links\nprint(chain)\n# prints out list of joint names\nprint(chain.get_joint_parameter_names())\n\n# specify joint values (can do so in many forms)\nth = [0.0, -math.pi / 4.0, 0.0, math.pi / 2.0, 0.0, math.pi / 4.0, 0.0]\n# do forward kinematics and get transform objects; end_only=False gives a dictionary of transforms for all links\nret = chain.forward_kinematics(th, end_only=False)\n# look up the transform for a specific link\ntg = ret['lbr_iiwa_link_7']\n# get transform matrix (1,4,4), then convert to separate position and unit quaternion\nm = tg.get_matrix()\npos = m[:, :3, 3]\nrot = pk.matrix_to_quaternion(m[:, :3, :3])\n```\n\nWe can parallelize FK by passing in 2D joint values, and also use CUDA if available\n```python\nimport torch\nimport pytorch_kinematics as pk\n\nd = \"cuda\" if torch.cuda.is_available() else \"cpu\"\ndtype = torch.float64\n\nchain = pk.build_serial_chain_from_urdf(open(\"kuka_iiwa.urdf\").read(), \"lbr_iiwa_link_7\")\nchain = chain.to(dtype=dtype, device=d)\n\nN = 1000\nth_batch = torch.rand(N, len(chain.get_joint_parameter_names()), dtype=dtype, device=d)\n\n# order of magnitudes faster when doing FK in parallel\n# elapsed 0.008678913116455078s for N=1000 when parallel\n# (N,4,4) transform matrix; only the one for the end effector is returned since end_only=True by default\ntg_batch = chain.forward_kinematics(th_batch)\n\n# elapsed 8.44686508178711s for N=1000 when serial\nfor i in range(N):\n tg = chain.forward_kinematics(th_batch[i])\n```\n\nWe can compute gradients through the FK\n```python\nimport torch\nimport math\nimport pytorch_kinematics as pk\n\nchain = pk.build_serial_chain_from_urdf(open(\"kuka_iiwa.urdf\").read(), \"lbr_iiwa_link_7\")\n\n# require gradient through the input joint values\nth = torch.tensor([0.0, -math.pi / 4.0, 0.0, math.pi / 2.0, 0.0, math.pi / 4.0, 0.0], requires_grad=True)\ntg = chain.forward_kinematics(th)\nm = tg.get_matrix()\npos = m[:, :3, 3]\npos.norm().backward()\n# now th.grad is populated\n```\n\nWe can load SDF and MJCF descriptions too, and pass in joint values via a dictionary (unspecified joints get th=0) for non-serial chains\n```python\nimport math\nimport torch\nimport pytorch_kinematics as pk\n\nchain = pk.build_chain_from_sdf(open(\"simple_arm.sdf\").read())\nret = chain.forward_kinematics({'arm_elbow_pan_joint': math.pi / 2.0, 'arm_wrist_lift_joint': -0.5})\n# recall that we specify joint values and get link transforms\ntg = ret['arm_wrist_roll']\n\n# can also do this in parallel\nN = 100\nret = chain.forward_kinematics({'arm_elbow_pan_joint': torch.rand(N, 1), 'arm_wrist_lift_joint': torch.rand(N, 1)})\n# (N, 4, 4) transform object\ntg = ret['arm_wrist_roll']\n\n# building the robot from a MJCF file\nchain = pk.build_chain_from_mjcf(open(\"ant.xml\").read())\nprint(chain)\nprint(chain.get_joint_parameter_names())\nth = {'hip_1': 1.0, 'ankle_1': 1}\nret = chain.forward_kinematics(th)\n\nchain = pk.build_chain_from_mjcf(open(\"humanoid.xml\").read())\nprint(chain)\nprint(chain.get_joint_parameter_names())\nth = {'left_knee': 0.0, 'right_knee': 0.0}\nret = chain.forward_kinematics(th)\n```\n\n## Jacobian calculation\nThe Jacobian (in the kinematics context) is a matrix describing how the end effector changes with respect to joint value changes\n(where 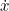 is the twist, or stacked velocity and angular velocity):\n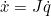 \n\nFor `SerialChain` we provide a differentiable and parallelizable method for computing the Jacobian with respect to the base frame.\n```python\nimport math\nimport torch\nimport pytorch_kinematics as pk\n\n# can convert Chain to SerialChain by choosing end effector frame\nchain = pk.build_chain_from_sdf(open(\"simple_arm.sdf\").read())\n# print(chain) to see the available links for use as end effector\n# note that any link can be chosen; it doesn't have to be a link with no children\nchain = pk.SerialChain(chain, \"arm_wrist_roll_frame\")\n\nchain = pk.build_serial_chain_from_urdf(open(\"kuka_iiwa.urdf\").read(), \"lbr_iiwa_link_7\")\nth = torch.tensor([0.0, -math.pi / 4.0, 0.0, math.pi / 2.0, 0.0, math.pi / 4.0, 0.0])\n# (1,6,7) tensor, with 7 corresponding to the DOF of the robot\nJ = chain.jacobian(th)\n\n# get Jacobian in parallel and use CUDA if available\nN = 1000\nd = \"cuda\" if torch.cuda.is_available() else \"cpu\"\ndtype = torch.float64\n\nchain = chain.to(dtype=dtype, device=d)\n# Jacobian calculation is differentiable\nth = torch.rand(N, 7, dtype=dtype, device=d, requires_grad=True)\n# (N,6,7)\nJ = chain.jacobian(th)\n\n# can get Jacobian at a point offset from the end effector (location is specified in EE link frame)\n# by default location is at the origin of the EE frame\nloc = torch.rand(N, 3, dtype=dtype, device=d)\nJ = chain.jacobian(th, locations=loc)\n```\n\nThe Jacobian can be used to do inverse kinematics. See [IK survey](https://www.math.ucsd.edu/~sbuss/ResearchWeb/ikmethods/iksurvey.pdf)\nfor a survey of ways to do so. Note that IK may be better performed through other means (but doing it through the Jacobian can give an end-to-end differentiable method).\n\n## Inverse Kinematics (IK)\nInverse kinematics is available via damped least squares (iterative steps with Jacobian pseudo-inverse damped to avoid oscillation near singularlities). \nCompared to other IK libraries, these are the typical advantages over them:\n- not ROS dependent (many IK libraries need the robot description on the ROS parameter server)\n- batched in both goal specification and retries from different starting configurations\n- goal orientation in addition to goal position\n\n\n\nSee `tests/test_inverse_kinematics.py` for usage, but generally what you need is below:\n```python\nfull_urdf = os.path.join(search_path, urdf)\nchain = pk.build_serial_chain_from_urdf(open(full_urdf).read(), \"lbr_iiwa_link_7\")\n\n# goals are specified as Transform3d poses in the **robot frame**\n# so if you have the goals specified in the world frame, you also need the robot frame in the world frame\npos = torch.tensor([0.0, 0.0, 0.0], device=device)\nrot = torch.tensor([0.0, 0.0, 0.0], device=device)\nrob_tf = pk.Transform3d(pos=pos, rot=rot, device=device)\n\n# specify goals as Transform3d poses in world frame\ngoal_in_world_frame_tf = ...\n# convert to robot frame (skip if you have it specified in robot frame already, or if world = robot frame)\ngoal_in_rob_frame_tf = rob_tf.inverse().compose(goal_tf)\n\n# get robot joint limits\nlim = torch.tensor(chain.get_joint_limits(), device=device)\n\n# create the IK object\n# see the constructor for more options and their explanations, such as convergence tolerances\nik = pk.PseudoInverseIK(chain, max_iterations=30, num_retries=10,\n joint_limits=lim.T,\n early_stopping_any_converged=True,\n early_stopping_no_improvement=\"all\",\n debug=False,\n lr=0.2)\n# solve IK\nsol = ik.solve(goal_in_rob_frame_tf)\n# num goals x num retries x DOF tensor of joint angles; if not converged, best solution found so far\nprint(sol.solutions)\n# num goals x num retries can check for the convergence of each run\nprint(sol.converged)\n# num goals x num retries can look at errors directly\nprint(sol.err_pos)\nprint(sol.err_rot)\n```\n\n## SDF Queries\nSee [pytorch-volumetric](https://github.com/UM-ARM-Lab/pytorch_volumetric) for the latest details, some instructions are pasted here:\n\nFor many applications such as collision checking, it is useful to have the\nSDF of a multi-link robot in certain configurations.\nFirst, we create the robot model (loaded from URDF, SDF, MJCF, ...) with\n[pytorch kinematics](https://github.com/UM-ARM-Lab/pytorch_kinematics).\nFor example, we will be using the KUKA 7 DOF arm model from pybullet data\n\n```python\nimport os\nimport torch\nimport pybullet_data\nimport pytorch_kinematics as pk\nimport pytorch_volumetric as pv\n\nurdf = \"kuka_iiwa/model.urdf\"\nsearch_path = pybullet_data.getDataPath()\nfull_urdf = os.path.join(search_path, urdf)\nchain = pk.build_serial_chain_from_urdf(open(full_urdf).read(), \"lbr_iiwa_link_7\")\nd = \"cuda\" if torch.cuda.is_available() else \"cpu\"\n\nchain = chain.to(device=d)\n# paths to the link meshes are specified with their relative path inside the URDF\n# we need to give them the path prefix as we need their absolute path to load\ns = pv.RobotSDF(chain, path_prefix=os.path.join(search_path, \"kuka_iiwa\"))\n```\n\nBy default, each link will have a `MeshSDF`. To instead use `CachedSDF` for faster queries\n\n```python\ns = pv.RobotSDF(chain, path_prefix=os.path.join(search_path, \"kuka_iiwa\"),\n link_sdf_cls=pv.cache_link_sdf_factory(resolution=0.02, padding=1.0, device=d))\n```\n\nWhich when the `y=0.02` SDF slice is visualized:\n\n\n\nWith surface points corresponding to:\n\n\n\n\nQueries on this SDF is dependent on the joint configurations (by default all zero).\n**Queries are batched across configurations and query points**. For example, we have a batch of\njoint configurations to query\n\n```python\nth = torch.tensor([0.0, -math.pi / 4.0, 0.0, math.pi / 2.0, 0.0, math.pi / 4.0, 0.0], device=d)\nN = 200\nth_perturbation = torch.randn(N - 1, 7, device=d) * 0.1\n# N x 7 joint values\nth = torch.cat((th.view(1, -1), th_perturbation + th))\n```\n\nAnd also a batch of points to query (same points for each configuration):\n\n```python\ny = 0.02\nquery_range = np.array([\n [-1, 0.5],\n [y, y],\n [-0.2, 0.8],\n])\n# M x 3 points\ncoords, pts = pv.get_coordinates_and_points_in_grid(0.01, query_range, device=s.device)\n```\n\nWe set the batch of joint configurations and query:\n\n```python\ns.set_joint_configuration(th)\n# N x M SDF value\n# N x M x 3 SDF gradient\nsdf_val, sdf_grad = s(pts)\n```\n\n\n# Credits\n- `pytorch_kinematics/transforms` is extracted from [pytorch3d](https://github.com/facebookresearch/pytorch3d) with minor extensions.\nThis was done instead of including `pytorch3d` as a dependency because it is hard to install and most of its code is unrelated.\n An important difference is that we use left hand multiplied transforms as is convention in robotics (T * pt) instead of their\n right hand multiplied transforms.\n- `pytorch_kinematics/urdf_parser_py`, and `pytorch_kinematics/mjcf_parser` is extracted from [kinpy](https://github.com/neka-nat/kinpy), as well as the FK logic.\nThis repository ports the logic to pytorch, parallelizes it, and provides some extensions.\n",
"bugtrack_url": null,
"license": "Copyright (c) 2023 University of Michigan ARM Lab Permission is hereby granted, free of charge, to any person obtaining a copy of this software and associated documentation files (the \"Software\"), to deal in the Software without restriction, including without limitation the rights to use, copy, modify, merge, publish, distribute, sublicense, and/or sell copies of the Software, and to permit persons to whom the Software is furnished to do so, subject to the following conditions: The above copyright notice and this permission notice shall be included in all copies or substantial portions of the Software. THE SOFTWARE IS PROVIDED \"AS IS\", WITHOUT WARRANTY OF ANY KIND, EXPRESS OR IMPLIED, INCLUDING BUT NOT LIMITED TO THE WARRANTIES OF MERCHANTABILITY, FITNESS FOR A PARTICULAR PURPOSE AND NONINFRINGEMENT. IN NO EVENT SHALL THE AUTHORS OR COPYRIGHT HOLDERS BE LIABLE FOR ANY CLAIM, DAMAGES OR OTHER LIABILITY, WHETHER IN AN ACTION OF CONTRACT, TORT OR OTHERWISE, ARISING FROM, OUT OF OR IN CONNECTION WITH THE SOFTWARE OR THE USE OR OTHER DEALINGS IN THE SOFTWARE. ",
"summary": "Robot kinematics implemented in pytorch",
"version": "0.7.4",
"project_urls": {
"Bug Reports": "https://github.com/UM-ARM-Lab/pytorch_kinematics/issues",
"Homepage": "https://github.com/UM-ARM-Lab/pytorch_kinematics",
"Source": "https://github.com/UM-ARM-Lab/pytorch_kinematics"
},
"split_keywords": [
"kinematics",
" pytorch",
" ik",
" fk",
" robotics"
],
"urls": [
{
"comment_text": "",
"digests": {
"blake2b_256": "54ce12c3b9c701fbfd10e9eaca47ab7a673bf71190eb0b39ac275433180acb78",
"md5": "442da94b3a62adc348a2ab933f6d6a49",
"sha256": "753fb81091d0692d763fef960305f6a0d5a343ec714da8d630f8479ab04f47aa"
},
"downloads": -1,
"filename": "pytorch_kinematics-0.7.4-py3-none-any.whl",
"has_sig": false,
"md5_digest": "442da94b3a62adc348a2ab933f6d6a49",
"packagetype": "bdist_wheel",
"python_version": "py3",
"requires_python": ">=3.6",
"size": 59649,
"upload_time": "2024-08-29T23:40:06",
"upload_time_iso_8601": "2024-08-29T23:40:06.232244Z",
"url": "https://files.pythonhosted.org/packages/54/ce/12c3b9c701fbfd10e9eaca47ab7a673bf71190eb0b39ac275433180acb78/pytorch_kinematics-0.7.4-py3-none-any.whl",
"yanked": false,
"yanked_reason": null
},
{
"comment_text": "",
"digests": {
"blake2b_256": "27059aae3bed03b6918394961fd0bf4c962676825f2bfca3e883475bdcc0cfd2",
"md5": "4038654a5619fa3a289d37258b989832",
"sha256": "34d45b51c1ead384b0a420a49d5bb92c2d838aa9a76cfc239369485bdcd65bd1"
},
"downloads": -1,
"filename": "pytorch_kinematics-0.7.4.tar.gz",
"has_sig": false,
"md5_digest": "4038654a5619fa3a289d37258b989832",
"packagetype": "sdist",
"python_version": "source",
"requires_python": ">=3.6",
"size": 66199,
"upload_time": "2024-08-29T23:40:07",
"upload_time_iso_8601": "2024-08-29T23:40:07.836010Z",
"url": "https://files.pythonhosted.org/packages/27/05/9aae3bed03b6918394961fd0bf4c962676825f2bfca3e883475bdcc0cfd2/pytorch_kinematics-0.7.4.tar.gz",
"yanked": false,
"yanked_reason": null
}
],
"upload_time": "2024-08-29 23:40:07",
"github": true,
"gitlab": false,
"bitbucket": false,
"codeberg": false,
"github_user": "UM-ARM-Lab",
"github_project": "pytorch_kinematics",
"travis_ci": false,
"coveralls": false,
"github_actions": true,
"lcname": "pytorch-kinematics"
}
